
Teorema di Torricelli in cosa consiste, formule ed esercizi
Il Teorema di Torricelli Il principio Torricelli afferma che la velocità del liquido che fuoriesce dal foro nella parete di una vasca o contenitore è identica a quella di un oggetto a cui è consentito cadere liberamente da un'altezza pari a quella del pelo libero del liquido fino al buco.
Il teorema è illustrato nella figura seguente:
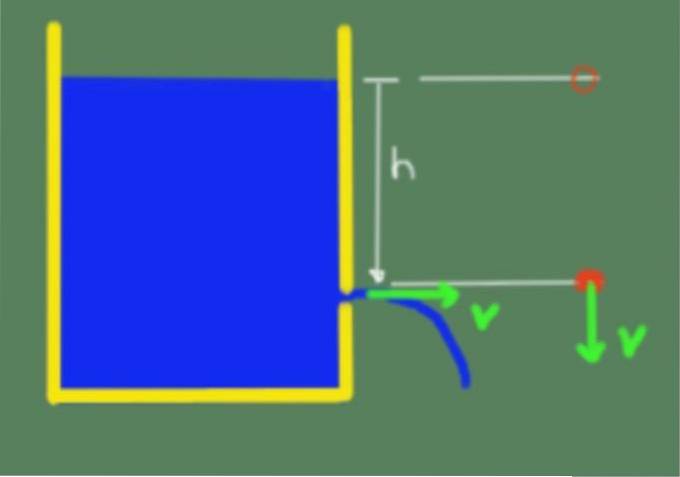
Per il teorema di Torricelli possiamo quindi affermare che la velocità di uscita del liquido attraverso un orifizio che si trova ad altezza h sotto la superficie libera del liquido è data dalla seguente formula:
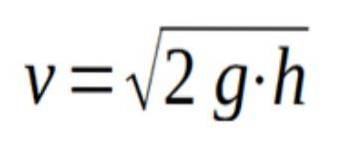
Dove g è l'accelerazione di gravità eh è l'altezza dal foro alla superficie libera del liquido.
Evangelista Torricelli era un fisico e matematico nato nella città di Faenza, Italia nel 1608. A Torricelli è attribuita l'invenzione del barometro a mercurio e in riconoscimento vi è un'unità di pressione chiamata "torr", equivalente a un millimetro di mercurio (mm di Hg).
Indice articolo
- 1 Dimostrazione del teorema
- 1.1 Caduta di oggetti
- 1.2 Liquido che esce dal foro
- 2 Esercizi risolti
- 2.1 Esercizio 1
- 3 I) Il piccolo tubo di uscita di un serbatoio d'acqua è 3 m sotto la superficie dell'acqua. Calcola la velocità di uscita dell'acqua.
- 3.1 Esercizio 2
- 3.2 Esercizio 3
- 4 Riferimenti
Dimostrazione del teorema
Nel teorema di Torricelli e nella formula che dà la velocità si assume che le perdite di viscosità siano trascurabili, così come in caduta libera si assume che l'attrito dovuto all'aria che circonda l'oggetto in caduta sia trascurabile..
L'ipotesi di cui sopra è ragionevole nella maggior parte dei casi e implica anche la conservazione dell'energia meccanica.
Per dimostrare il teorema, troveremo prima la formula per la velocità di un oggetto che viene rilasciato con velocità iniziale zero, dalla stessa altezza della superficie del liquido nel serbatoio..
Il principio di conservazione dell'energia verrà applicato per ottenere la velocità dell'oggetto che cade proprio quando è sceso di quota h uguale a quello da foro a superficie libera.
Non essendoci perdite per attrito è valido applicare il principio di conservazione dell'energia meccanica. Supponiamo che l'oggetto in caduta abbia massa m e l'altezza h sia misurata dal livello di uscita del liquido.
Oggetto che cade
Quando l'oggetto viene rilasciato da un'altezza pari a quella della superficie libera del liquido, la sua energia è solo potenziale gravitazionale, poiché la sua velocità è zero e quindi la sua energia cinetica è zero. L'energia potenziale Ep è data da:
Ep = m g h
Quando passa davanti al foro, la sua altezza è zero, quindi l'energia potenziale è zero, quindi ha solo l'energia cinetica Ec data da:
Ec = ½ m vDue
Poiché l'energia si conserva Ep = Ec da quanto si ottiene:
½ m vDue = m g h
Risolvendo per la velocità v si ottiene quindi la formula Torricelli:
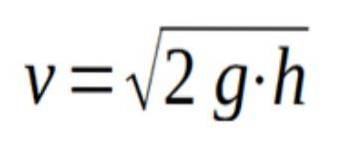
Liquido che esce dal buco
Successivamente troveremo la velocità di uscita del liquido attraverso il foro, in modo da mostrare che coincide con quella appena calcolata per un oggetto in caduta libera.
Per questo ci baseremo sul principio di Bernoulli, che altro non è che la conservazione dell'energia applicata ai fluidi.
Il principio di Bernoulli è formulato in questo modo:
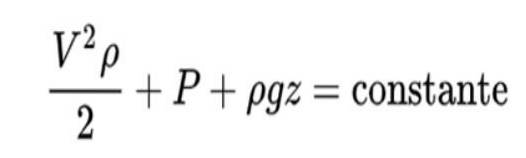
L'interpretazione di questa formula è la seguente:
- Il primo termine rappresenta l'energia cinetica del fluido per unità di volume
- Il secondo rappresenta il lavoro svolto dalla pressione per unità di area della sezione trasversale.
- Il terzo rappresenta l'energia potenziale gravitazionale per unità di volume di fluido..
Partendo dal presupposto che si tratta di un fluido ideale, in condizioni non turbolente con velocità relativamente basse, è pertinente affermare che l'energia meccanica per unità di volume nel fluido è costante in tutte le regioni o sezioni trasversali del stesso..
In questa formula V è la velocità del fluido, ρ la densità del fluido, P pressione e z posizione verticale.
La figura sotto mostra la formula di Torricelli partendo dal principio di Bernoulli.
Applichiamo la formula di Bernoulli sulla superficie libera del liquido indicata con (1) e sul foro di uscita indicato con (2). Il livello di prevalenza zero è stato scelto a filo con il foro di uscita.
Partendo dalla premessa che la sezione trasversale in (1) è molto più grande che in (2), possiamo quindi supporre che la velocità di discesa del liquido in (1) sia praticamente trascurabile.
Questo è il motivo per cui V1= 0, la pressione a cui è sottoposto il liquido in (1) è la pressione atmosferica e l'altezza misurata dall'orifizio è h.
Per la sezione di uscita (2) assumiamo che la velocità di uscita sia v, anche la pressione a cui è sottoposto il liquido in uscita è pressione atmosferica e l'altezza di uscita è zero.
I valori corrispondenti alle sezioni (1) e (2) sono sostituiti nella formula di Bernoulli e posti uguali. L'uguaglianza vale perché assumiamo che il fluido sia ideale e non ci siano perdite per attrito viscoso. Una volta semplificati tutti i termini, si ottiene la velocità al foro di uscita.
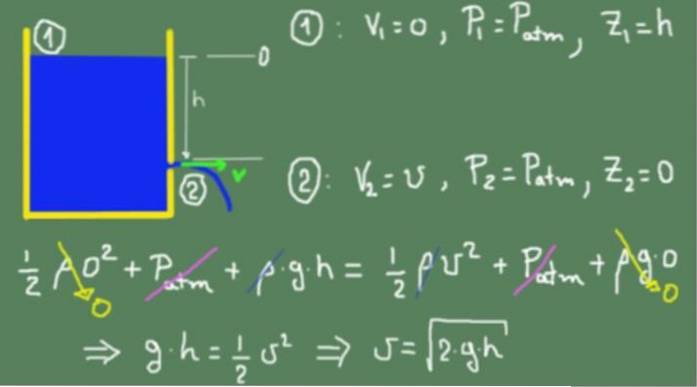
Il riquadro sopra mostra che il risultato ottenuto è lo stesso di un oggetto in caduta libera,
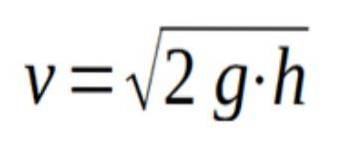
Esercizi risolti
Esercizio 1
io) Il piccolo tubo di uscita di un serbatoio dell'acqua si trova 3 m sotto la superficie dell'acqua. Calcola la velocità di uscita dell'acqua.
Soluzione:
La figura seguente mostra come la formula di Torricelli viene applicata a questo caso.
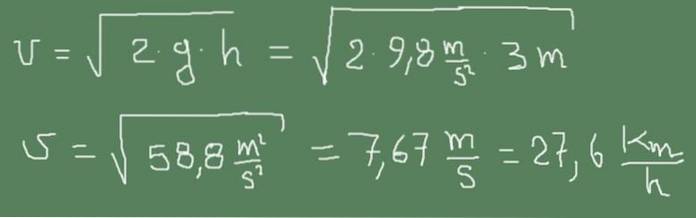
Esercizio 2
II) Supponendo che il tubo di uscita del serbatoio dell'esercizio precedente abbia un diametro di 1 cm, calcolare la portata dell'acqua in uscita.
Soluzione:
La portata è il volume di liquido in uscita nell'unità di tempo e si calcola semplicemente moltiplicando l'area dell'orifizio di uscita per la velocità di uscita.
La figura seguente mostra i dettagli del calcolo.

Esercizio 3
III) Determina quanto è alta la superficie libera dell'acqua in un contenitore, se lo sai
che in un foro nel fondo del contenitore l'acqua esce a 10 m / s.
Soluzione:
Anche quando il foro si trova sul fondo del contenitore, è comunque possibile applicare la formula Torricelli.
La figura seguente mostra il dettaglio dei calcoli.

Riferimenti
- Wikipedia. Teorema di Torricelli.
- Hewitt, P. Scienza fisica concettuale. Quinta edizione.119.
- Giovane, Hugh. 2016. Sears-Zemansky's University Physics with Modern Physics. 14a edizione. Pearson. 384.


Nessun utente ha ancora commentato questo articolo.