
Teorema di Green, dimostrazione, applicazioni ed esercizi
Il Teorema di Green è un metodo di calcolo utilizzato per mettere in relazione gli integrali di linea con la doppia area o gli integrali di superficie. Le funzioni coinvolte devono essere denotate come campi vettoriali e definite all'interno del percorso C.
Ad esempio, un'espressione integrale di riga può essere molto difficile da risolvere; tuttavia implementando il teorema di Green, i doppi integrali diventano piuttosto basilari. È sempre importante rispettare la direzione positiva della traiettoria, questa si riferisce alla direzione antioraria.

Il teorema di Green è un caso particolare del teorema di Stokes, dove la proiezione della funzione vettoriale viene eseguita nel piano xy.
Indice articolo
- 1 Definizione
- 2 Demo
- 3 Applicazioni
- 4 Storia
- 5 Relazione con altri teoremi
- 6 esercizi
- 7 Riferimenti
Definizione
L'espressione del teorema di Green è la seguente:
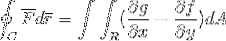
Il primo termine indica l'integrale di linea definito dal percorso “C”, del prodotto scalare tra la funzione vettoriale “F” e quella del vettore “r”.
C: È il percorso definito su cui verrà proiettata la funzione vettoriale fintanto che è definita per quel piano.
F: funzione vettoriale, dove ciascuna delle sue componenti è definita da una funzione come tale (f, g).
r: È un vettore tangente alla regione R su cui è definito l'integrale. In questo caso operiamo con un differenziale di questo vettore.
Nel secondo termine vediamo sviluppato il teorema di Green, dove si osserva il doppio integrale definito nella regione R della differenza delle derivate parziali di g e f, rispettivamente rispetto a xey. Per un differenziale di area che altro non è che il prodotto di entrambi i differenziali bidimensionali (dx.dy).
Questo teorema è perfettamente applicabile per lo spazio e gli integrali di superficie.
Dimostrazione
Per dimostrare il teorema di Green in modo semplice, questo compito sarà suddiviso in 2 parti. Per prima cosa assumeremo che la funzione vettoriale F abbia definizione solo nel versore io. Mentre la funzione "g" corrisponde al versore j sarà uguale a zero.
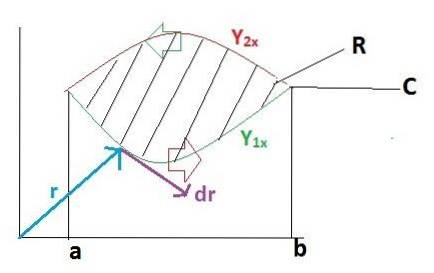
F = f (x, y)io + g (x, y)j = f (x, y)io + 0
r = xio + Yj
dr = dxio + dyj
Per prima cosa sviluppiamo la retta integrale sulla traiettoria C, per la quale la traiettoria è stata settorizzata in 2 sezioni che vanno prima da a a be poi da b ad a.
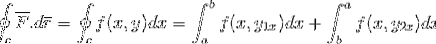
La definizione del teorema fondamentale del calcolo è applicata per un integrale definito.
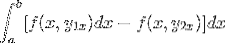
L'espressione viene riordinata in un unico integrale, il negativo diventa un fattore comune e l'ordine dei fattori viene invertito.
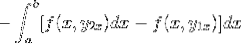
Osservando in dettaglio questa espressione, diventa evidente che quando si applicano i criteri della funzione primitiva, siamo in presenza dell'integrale dell'espressione derivata da f rispetto a y. Valutato in parametri
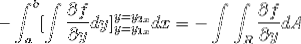
Ora è sufficiente supporre che la funzione vettoriale F sia definita solo per g (x, y)j. Laddove operando in maniera analoga al caso precedente si ottiene quanto segue:
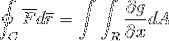
Per finire, le 2 prove vengono prese e unite nel caso in cui la funzione vettoriale assume valori per entrambi i versori. In questo modo si mostra come la retta integrale dopo essere stata definita e considerata come una traiettoria unidimensionale, possa essere completamente sviluppata per il piano e lo spazio.
F = f (x, y)io + g (x, y)j
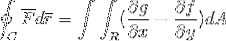
In questo modo viene dimostrato il teorema di Green.
Applicazioni
Le applicazioni del teorema di Green sono ampie nei rami della fisica e della matematica. Questi si estendono a qualsiasi applicazione o utilizzo che può essere dato all'integrazione di linea.
Il lavoro meccanico svolto da una forza F attraverso un percorso C, può essere sviluppato da un integrale di linea che è espresso come doppio integrale di un'area mediante il teorema di Green.
I momenti di inerzia di molti corpi soggetti a forze esterne in diversi punti di applicazione rispondono anche a integrali di linea che possono essere sviluppati con il teorema di Green..
Questo ha molteplici funzionalità negli studi di resistenza dei materiali in uso. Dove i valori esterni possono essere quantificati e presi in considerazione prima dell'elaborazione di vari elementi.
In generale, il teorema di Green facilita la comprensione e la definizione delle aree in cui le funzioni vettoriali sono definite rispetto a una regione secondo una traiettoria.
Storia
È stato pubblicato nel 1828 nell'opera Analisi matematica alle teorie dell'elettricità e del magnetismo, scritto dal matematico britannico George Green. In esso vengono esplorate sezioni abbastanza decisive nell'applicazione del calcolo in fisica, come il concetto di funzioni potenziali, le funzioni di Green e le applicazioni del suo omonimo teorema.
George Green ha ufficializzato la sua carriera da studente all'età di 40 anni, essendo fino ad ora un matematico completamente autodidatta. Dopo gli studi presso l'Università di Cambridge, ha continuato la sua ricerca, apportando contributi su acustica, ottica e idrodinamica che sono ancora validi oggi..
Relazione con altri teoremi
Il teorema di Green è un caso speciale e deriva da altri 2 teoremi molto importanti nel campo del calcolo. Questi sono il teorema di Kelvin-Stokes e il teorema della divergenza o Gauss Ostrogradski.
Partendo da uno dei due teoremi è possibile arrivare al teorema di Green. Alcune definizioni e proposizioni sono necessarie per sviluppare tali prove..
Formazione
- L'esercizio seguente mostra come trasformare un integrale di retta in un integrale doppio rispetto a una regione R.
L'espressione originale è la seguente:
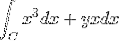
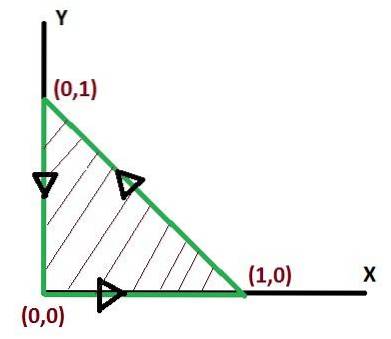
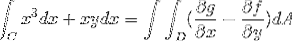
Da dove vengono prese le funzioni corrispondenti af e g
f (x, y) = x3 g (x, y) = yx
df / dy = 0 dg / dx = y
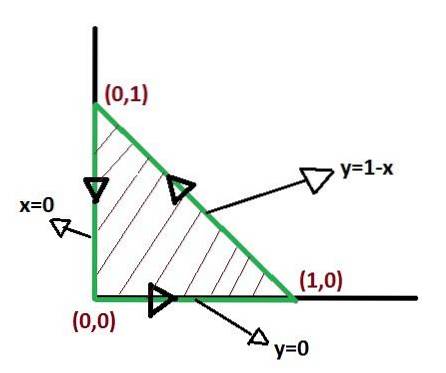
Non esiste un unico modo per definire i limiti dell'integrazione quando si applica il teorema di Green. Ma ci sono modi in cui gli integrali dopo essere stati definiti possono essere più semplici. Quindi l'ottimizzazione dei limiti di integrazione merita attenzione.
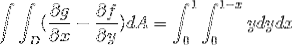
Dove risolvendo gli integrali otteniamo:
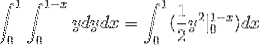
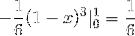
Questo valore corrisponde in unità cubiche alla regione sotto la funzione vettoriale e sopra la regione triangolare definita da C.
Per il caso dell'integrale di linea senza eseguire il metodo di Green, sarebbe stato necessario parametrizzare le funzioni in ogni sezione della regione. Cioè, eseguire 3 integrali parametrizzati per la risoluzione. Questa è una prova sufficiente dell'efficacia che Robert Green ha portato con il suo teorema al calcolo.
Riferimenti
- Introduzione alla meccanica dei continui. W Michael Lai, David H. Rubin, Erhard Krempl, David Rubin Butterworth-Heinemann, 23 luglio. 2009
- Calcolo multivariabile. James Stewart. Cengage Learning, 22 marzo 2011
- Una storia informale del teorema di Green e delle idee associate. James Joseph Cross. Dipartimento di Matematica, Università di Melbourne, 1975
- Conduzione del calore mediante funzioni verdi. Kevin D.Cole, James V. Beck, A. Haji-Sheikh, Bahman Litkouhi. Taylor & Francis, 16 luglio 2010
- Applicazione del teorema di Green all'estremizzazione degli integrali lineari. Centro di informazione tecnica della difesa, 1961


Nessun utente ha ancora commentato questo articolo.