Il Teorema di Bolzano stabilisce che se una funzione è continua in tutti i punti di un intervallo chiuso [a, b] ed è vero che l'immagine di "a" e "b" (sotto la funzione) hanno segni opposti, allora ci sarà almeno uno punto "C" nell'intervallo aperto (a, b), in modo tale che la funzione valutata in "c" sia uguale a 0.
Questo teorema fu enunciato dal filosofo, teologo e matematico Bernard Bolzano nel 1850. Questo scienziato, nato nell'odierna Repubblica Ceca, fu uno dei primi matematici della storia a fornire una prova formale delle proprietà delle funzioni continue..
Indice articolo
Il teorema di Bolzano è anche noto come teorema dei valori intermedi, che aiuta nella determinazione di valori specifici, in particolare zeri, di alcune funzioni reali di una variabile reale.
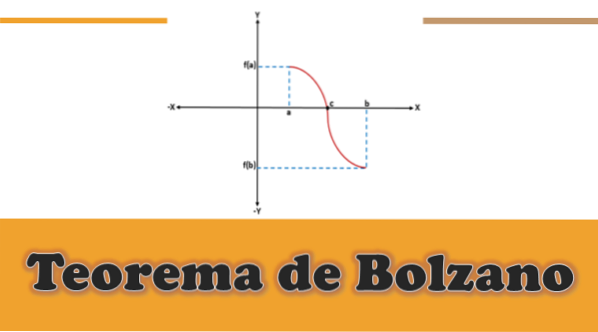
In una data funzione f (x) continua - cioè che f (a) e f (b) sono collegati da una curva-, dove f (a) è sotto l'asse x (è negativo), e f ( b) sopra l'asse x (è positivo), o viceversa, graficamente ci sarà un punto di taglio sull'asse x che rappresenterà un valore intermedio "c", che sarà compreso tra "a" e "B" e il valore di f (c) sarà uguale a 0.
Analizzando graficamente il teorema di Bolzano si può notare che per ogni funzione continua f definita su un intervallo [a, b], dove f (a)*f (b) è minore di 0, ci sarà almeno una radice "c" di quella funzione nell'intervallo (a, b).
Questo teorema non stabilisce il numero di punti in quell'intervallo aperto, afferma solo che c'è almeno 1 punto.
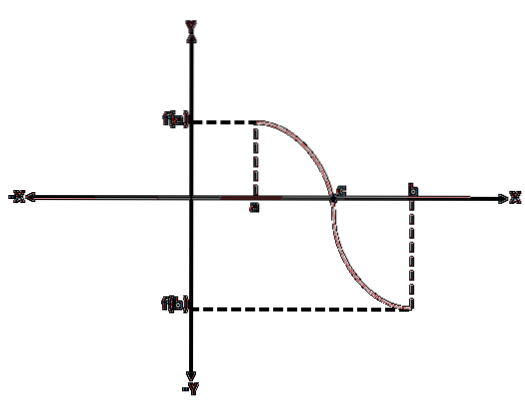
Per dimostrare il teorema di Bolzano, si assume senza perdita di generalità che f (a) < 0 y f(b) > 0; quindi, possono esserci molti valori tra "a" e "b" per i quali f (x) = 0, ma è solo necessario mostrare che ce n'è uno.
Iniziamo valutando f nel punto medio (a + b) / 2. Se f ((a + b) / 2) = 0 allora la dimostrazione finisce qui; altrimenti, allora f ((a + b) / 2) è positivo o negativo.
Si sceglie una delle metà dell'intervallo [a, b], in modo tale che i segni della funzione valutati agli estremi siano differenti. Questo nuovo intervallo sarà [a1, b1].
Ora, se f valutato nel punto medio di [a1, b1] non è zero, allora viene eseguita la stessa operazione di prima; cioè, viene scelta la metà di questo intervallo che soddisfa la condizione dei segni. Lascia che questo nuovo intervallo sia [a2, b2].
Se continui con questo processo, avrai due sequenze an e bn, tali che:
an sta aumentando e bn sta diminuendo:
a ≤ a1 ≤ a2 ≤… ≤ an ≤…. ≤…. ≤ bn ≤…. ≤ b2 ≤ b1 ≤ b.
Se si calcola la lunghezza di ogni intervallo [ai, bi], avremo:
b1-a1 = (b-a) / 2.
b2-a2 = (b-a) / 2².
... .
bn-an = (b-a) / 2 ^ n.
Pertanto, il limite per n tende all'infinito di (bn-an) è uguale a 0.
Usando che an è crescente e limitato e bn è decrescente e limitato, abbiamo che esiste un valore "c" tale che:
a ≤ a1 ≤ a2 ≤… ≤ an ≤… .≤ c ≤…. ≤ bn ≤…. ≤ b2 ≤ b1 ≤ b.
Il limite di an è "c" e anche il limite di bn è "c". Quindi, dato ogni δ> 0, c'è sempre una "n" tale che l'intervallo [an, bn] sia contenuto all'interno dell'intervallo (c-δ, c + δ).
Ora, si deve dimostrare che f (c) = 0.
Se f (c)> 0, allora poiché f è continua, esiste un ε> 0 tale che f è positivo sull'intero intervallo (c-ε, c + ε). Tuttavia, come detto sopra, esiste un valore "n" tale che f cambia segno in [an, bn] e, inoltre, [an, bn] è contenuto all'interno di (c-ε, c + ε), che è un contraddizione.
Se f (c) < 0, entonces como f es continua, existe un ε >0 tale che f è negativo per tutto l'intervallo (c-ε, c + ε); ma esiste un valore "n" tale che f cambia segno in [an, bn]. Si scopre che [an, bn] è contenuto all'interno di (c-ε, c + ε), che è anche una contraddizione.
Pertanto, f (c) = 0 e questo è ciò che volevamo mostrare.
Dalla sua interpretazione grafica, il teorema di Bolzano viene utilizzato per trovare radici o zeri in una funzione continua, tramite bisezione (approssimazione), che è un metodo di ricerca incrementale che divide sempre gli intervalli per 2.
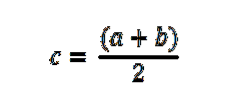
Quindi viene preso un intervallo [a, c] o [c, b] nel punto in cui avviene il cambio di segno e il processo viene ripetuto fino a quando l'intervallo è sempre più piccolo, in modo da avvicinarsi al valore desiderato; cioè al valore che la funzione rende 0.
In sintesi, per applicare il teorema di Bolzano e quindi trovare le radici, limitare gli zeri di una funzione o dare una soluzione a un'equazione, vengono eseguiti i seguenti passaggi:
- Si verifica se f è una funzione continua sull'intervallo [a, b].
- Se l'intervallo non è dato, deve essere trovato dove la funzione è continua.
- Si verifica se gli estremi dell'intervallo danno segni opposti quando valutati in f.
- Se non si ottengono segni opposti, l'intervallo deve essere diviso in due sottointervalli utilizzando il punto medio.
- Valutare la funzione nel punto medio e verificare che l'ipotesi di Bolzano sia soddisfatta, dove f (a) * f (b) < 0.
- A seconda del segno (positivo o negativo) del valore trovato, il processo si ripete con un nuovo sottointervallo fino a soddisfare l'ipotesi di cui sopra..
Determina se la funzione f (x) = xDue - 2, ha almeno una soluzione reale nell'intervallo [1,2].
Abbiamo la funzione f (x) = xDue - 2. Poiché è polinomiale, significa che è continuo su qualsiasi intervallo.
Viene chiesto di determinare se ha una soluzione reale nell'intervallo [1, 2], quindi ora è solo necessario sostituire gli estremi dell'intervallo nella funzione per conoscere il segno di questi e per sapere se soddisfano la condizione di essere diversi:
f (x) = xDue - Due
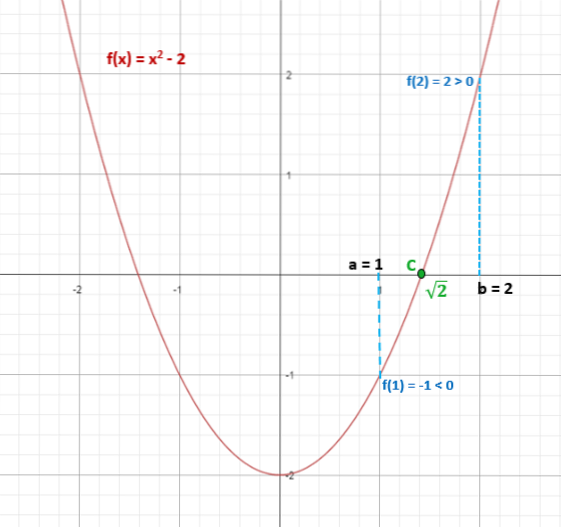
f (1) = 1Due - 2 = -1 (negativo)
f (2) = 2Due - 2 = 2 (positivo)
Pertanto, segno di f (1) ≠ segno f (2).
Questo assicura che ci sia almeno un punto "c" che appartiene all'intervallo [1,2], in cui f (c) = 0.
In questo caso, il valore di "c" può essere facilmente calcolato come segue:
XDue - 2 = 0
x = ± √2.
Quindi, √2 ≈ 1,4 appartiene all'intervallo [1,2] e soddisfa che f (√2) = 0.
Mostra che l'equazione x5 + x + 1 = 0 ha almeno una soluzione reale.
Notiamo prima che f (x) = x5 + x + 1 è una funzione polinomiale, il che significa che è continua su tutti i numeri reali.
In questo caso non viene fornito alcun intervallo, quindi i valori devono essere scelti intuitivamente, preferibilmente vicini a 0, per valutare la funzione e trovare le variazioni di segno:
Se utilizzi l'intervallo [0, 1] devi:
f (x) = x5 + x + 1.
f (0) = 05 + 0 + 1 = 1> 0.
f (1) = 15 + 1 + 1 = 3> 0.
Poiché non vi è alcun cambiamento di segno, il processo viene ripetuto con un altro intervallo.
Se usi l'intervallo [-1, 0] devi:
f (x) = x5 + x + 1.
f (-1) = (-1)5 + (-1) + 1 = -1 < 0.
f (0) = 05 + 0 + 1 = 1> 0.
In questo intervallo c'è un cambio di segno: segno di f (-1) ≠ segno di f (0), il che significa che la funzione f (x) = x5 + x + 1 ha almeno una radice reale "c" nell'intervallo [-1, 0], tale che f (c) = 0. In altre parole, è vero che x5 + x + 1 = 0 ha una soluzione reale nell'intervallo [-1,0].
Nessun utente ha ancora commentato questo articolo.