
Somma di polinomi, come si fa, esempi, esercizi
Il somma di polinomi è l'operazione che consiste nell'aggiungere due o più polinomi, risultando in un altro polinomio. Per eseguirlo è necessario aggiungere i termini dello stesso ordine di ciascuno dei polinomi e indicare la somma risultante.
Rivediamo prima brevemente il significato di "termini dello stesso ordine". Qualsiasi polinomio è costituito da addizioni e / o sottrazioni di termini.

I termini possono essere prodotti di numeri reali e una o più variabili, rappresentate da lettere, ad esempio: 3xDue e -√5.aDueavanti Cristo3 sono termini.
Ebbene, i termini dello stesso ordine sono quelli che hanno lo stesso esponente o potenza, sebbene possano avere un coefficiente diverso.
-I termini di ordine uguale sono: 5x3, √2 x3 e -1 / 2x3
-Termini di ordine diversi: -2x-Due, 2xy-1 e √6xDueY
È importante tenere presente che è possibile aggiungere o sottrarre solo termini dello stesso ordine, operazione nota come riduzione. Altrimenti la somma viene semplicemente lasciata indicata.
Una volta chiarito il concetto di termini dello stesso ordine, i polinomi vengono aggiunti seguendo questi passaggi:
-Ordine Dapprima i polinomi da sommare, tutti allo stesso modo, in modo crescente o decrescente, cioè con le potenze da inferiore a superiore o viceversa.
-Completare, nel caso in cui manchi l'alimentazione nella sequenza.
-Ridurre termini simili.
-Indicare la somma risultante.
Indice articolo
- 1 Esempi di addizione di polinomi
- 1.1 Aggiungere due o più polinomi con più di una variabile
- 2 Esercizi per l'aggiunta di polinomi
- 2.1 - Esercizio 1
- 2.2 - Esercizio 2
- 3 Riferimenti
Esempi di addizione di polinomi
Inizieremo aggiungendo due polinomi con una singola variabile chiamata X, ad esempio i polinomi P (x) e Q (x) dati da:
P (x) = 2xDue - 5x4 + 2x -x5 - 3x3 +12
Q (x) = x5- 25 x + xDue
Seguendo i passaggi descritti, inizierai ordinandoli in ordine decrescente, che è il modo più comune:
P (x) = -x5- 5x4 - 3x3 + 2xDue + 2x +12
Q (x) = x5+ XDue - 25x
Il polinomio Q (x) non è completo, si vede che mancano potenze con esponenti 4, 3 e 0. Quest'ultimo è semplicemente il termine indipendente, quello che non ha lettera.
Q (x) = x5+ 0x4 + 0x3 + XDue - 25x + 0
Una volta terminato questo passaggio, sono pronti per l'aggiunta. Puoi aggiungere i termini simili e quindi indicare la somma, oppure posizionare i polinomi ordinati uno sotto l'altro e ridurre per colonne, in questo modo:
- X5 - 5x4 - 3x3 + 2xDue + 2x +12
+ X5 + 0x4 + 0x3 + XDue - 25x + 0 +
--
0x5-5x4 - 3x3 +3xDue - 23x + 12 = P (x) + Q (x)
È importante notare che quando viene aggiunto, viene fatto rispettando algebricamente la regola dei segni, in questo modo 2x + (-25 x) = -23x. Cioè, se i coefficienti hanno un segno diverso, vengono sottratti e il risultato porta il segno del maggiore.
Aggiungi due o più polinomi con più di una variabile
Quando si tratta di polinomi con più di una variabile, una di esse viene scelta per ordinarla. Ad esempio, supponi di chiedere di aggiungere:
R (x, y) = 5xDue - 4yDue + 8xy - 6y3
Y:
T (x, y) = ½ xDue- 6yDue - 11xy + x3Y
Viene scelta una delle variabili, ad esempio x per ordinare:
R (x, y) = 5xDue + 8xy - 6y3 - 4yDue
T (x, y) = + x3y + ½ xDue - 11xy - 6yDue
Immediatamente vengono completati i termini mancanti, secondo i quali ogni polinomio ha:
R (x, y) = 0x3y + 5xDue + 8xy - 6y3 - 4yDue
T (x, y) = + x3y + ½ xDue - 11xy + 0y3 - 6yDue
E siete entrambi pronti a ridurre termini simili:
0x3y + 5xDue + 8xy - 6y3 - 4yDue
+ X3y + ½ xDue - 11xy + 0y3 - 6yDue +
-
+ X3e + 11 / 2xDue - 3xy - 6y3 - 10yDue = R (x, y) + T (x, y)
Esercizi di addizione polinomiale
- Esercizio 1
Nella seguente somma di polinomi, indicare il termine che deve andare nello spazio vuoto per ottenere la somma dei polinomi:
-5x4 + 0x3 + 2xDue + 1
X5 + 2x4 - 21xDue + 8x - 3
2x5 +9x3 -14x
-
-6x5+10x4 -0x3 + 5xDue - 11x + 21
Soluzione
Per ottenere -6x5 è richiesto un termine della forma ascia5, tale che:
a + 1+ 2 = -6
Perciò:
a = -6-1-2 = -9
E il termine di ricerca è:
-9x5
-Procedi in modo simile per trovare il resto dei termini. Ecco quello per l'esponente 4:
-5 + 2 + a = 10 → a = 10 + 5-2 = 13
Il termine mancante è: 13x4.
-Per i poteri di x3 è immediato che il termine debba essere -9x3, quindi il coefficiente del termine cubo è 0.
-Per quanto riguarda le potenze al quadrato: a + 8-14 = -11 → a = -11-8 + 14 = -5 e il termine è -5xDue.
-Il termine lineare si ottiene mediante a +8-14 = -11 → a = -11 + 14-8 = -5, il termine mancante è -5x.
-Infine il termine indipendente è: 1-3 + a = -21 → a = -19.
- Esercizio 2
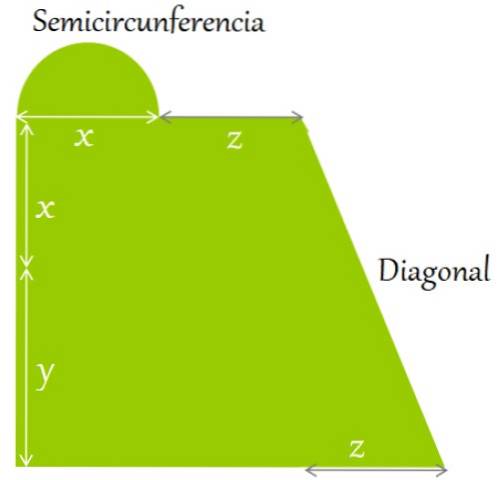
Un terreno pianeggiante è recintato come mostrato in figura. Trova un'espressione per:
a) Il perimetro e
b) La sua area, nei termini delle lunghezze indicate:
Soluzione a
Il perimetro è definito come la somma dei lati e dei contorni della figura. Partendo dall'angolo in basso a sinistra, in senso orario, abbiamo:
Perimetro = y + x + lunghezza semicerchio + z + lunghezza diagonale + z + z + x
Il semicerchio ha un diametro pari a x. Poiché il raggio è la metà del diametro, dobbiamo:
Raggio = x / 2.
La formula per la lunghezza di una circonferenza completa è:
L = 2π x raggio
Poi:
Lunghezza del semicerchio = ½. 2π (x / 2) = πx / 2
Da parte sua, la diagonale è calcolata con il teorema di Pitagora applicato ai lati: (x + y) che è il lato verticale e z, che è l'orizzontale:
Diagonale = [(x + y)Due + zDue]1/2
Queste espressioni vengono sostituite in quella per il perimetro, per ottenere:
Perimetro = y + x + πx / 2 + z + [(x + y)Due + zDue]1/2+ z + x + z
I termini simili sono ridotti, poiché l'aggiunta richiede che il risultato sia semplificato il più possibile:
Perimetro = y + [x + π (x / 2) + x] + z + z + z + [(x + y)Due + zDue]1/2 = y + (2 + π / 2) x + 3z
Soluzione b
L'area risultante è la somma dell'area del rettangolo, del semicerchio e del triangolo rettangolo. Le formule per queste aree sono:
-Rettangolo: base x altezza
-Semicerchio: ½ π (raggio)Due
-Triangolo: base x altezza / 2
Area rettangolo
(x + y). (x + z) = xDue + xz + yx + yz
Area semicerchio
½ π (x / 2)Due = π xDue / 8
Area del triangolo
½ z (x + y) = ½ zx + ½ zy
Area totale
Per trovare l'area totale, vengono aggiunte le espressioni trovate per ciascuna area parziale:
Area totale = xDue + xz + yx + yz + (π xDue / 8) + ½ zx + ½ zy
E infine si riducono tutti i termini simili:
Area totale = (1 + π / 8) xDue + 3/2 xy + 3 / 2yz + yx
Riferimenti
- Baldor, A. 1991. Algebra. Editoriale Culturale Venezolana S.A.
- Jiménez, R. 2008. Algebra. Prentice Hall.
- La matematica è divertente Aggiungere e sottrarre polinomi. Estratto da: mathsisfun.com.
- Monterey Institute. Somma e sottrazione di polinomi. Estratto da: montereyinstitute.org.
- UC Berkeley. Algebra dei polinomi. Estratto da: math.berkeley.edu.



Nessun utente ha ancora commentato questo articolo.