
Storia del sistema ottale, sistema di numerazione, conversioni
Il sistema ottale è un sistema di numerazione posizionale in base otto (8); cioè, consiste di otto cifre, che sono: 0, 1, 2, 3, 4, 5, 6 e 7. Pertanto, ogni cifra di un numero ottale può avere qualsiasi valore da 0 a 7. I numeri ottali sono formati da numeri binari.
Questo perché la sua base è una potenza esatta di due (2). Cioè, i numeri che appartengono al sistema ottale si formano quando sono raggruppati in tre cifre consecutive, ordinate da destra a sinistra, ottenendo così il loro valore decimale..

Indice articolo
- 1 Storia
- 2 Sistema di numerazione ottale
- 3 Conversione da ottale a decimale
- 3.1 Esempio 1
- 3.2 Esempio 2
- 4 Conversione da sistema decimale a ottale
- 4.1 Esempio
- 5 Conversione da ottale a sistema binario
- 6 Conversione da sistema binario a sistema ottale
- 7 Conversione da ottale a esadecimale e viceversa
- 7.1 Esempio
- 8 Riferimenti
Storia
Il sistema ottale ha la sua origine in tempi antichi, quando le persone usavano le mani per contare gli animali da otto a otto.
Ad esempio, per contare il numero di vacche in una stalla, si comincia a contare con la mano destra, unendo il pollice con il mignolo; quindi per contare il secondo animale si univa il pollice con l'indice, e così via con le restanti dita di ciascuna mano, fino a completare 8.
C'è la possibilità che anticamente il sistema di numerazione ottale fosse utilizzato prima del decimale per poter contare gli spazi interdigitali; cioè conta tutte le dita tranne i pollici.
Successivamente è stato stabilito il sistema di numerazione ottale, che ha avuto origine dal sistema binario, perché ha bisogno di molte cifre per rappresentare un solo numero; da allora sono stati creati i sistemi ottale ed esagonale, che non richiedono così tante cifre e possono essere facilmente convertiti nel sistema binario.
Sistema di numerazione ottale
Il sistema ottale è composto da otto cifre che vanno da 0 a 7. Queste hanno lo stesso valore del sistema decimale, ma il loro valore relativo cambia a seconda della posizione che occupano. Il valore di ogni posizione è dato dalle potenze in base 8.
Le posizioni delle cifre in un numero ottale hanno i seguenti pesi:
84, 83, 8Due, 81, 80, punto ottale, 8-1, 8-Due, 8-3, 8-4, 8-5.
La cifra ottale più grande è 7; in questo modo, quando si conteggia in questo sistema, la posizione di una cifra viene incrementata da 0 a 7. Al raggiungimento di 7, viene riciclata a 0 per il conteggio successivo; in questo modo viene incrementata la posizione della cifra successiva. Ad esempio, per contare le sequenze, nel sistema ottale sarà:
- 0, 1, 2, 3, 4, 5, 6, 7, 10.
- 53, 54, 55, 56, 57, 60.
- 375, 376, 377, 400.
C'è un teorema fondamentale che viene applicato al sistema ottale, ed è espresso come segue:
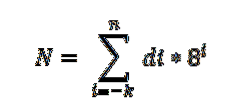
In questa espressione di rappresenta la cifra moltiplicata per la potenza di base 8, che indica il valore di posizione di ciascuna cifra, nello stesso modo in cui è ordinata nel sistema decimale.
Ad esempio, hai il numero 543,2. Per portarlo al sistema ottale, si scompone come segue:
N = ∑ [(5 * 8Due) + (4 * 81) + (3 *80) + (2 *8-1)] = (5 * 64) + (4 * 8) + (2 * 1) + (2 * 0,125)
N = 320 +32 + 2 + 0,25 = 354 + 0,25d
In questo modo devi 543.2che cosa = 354,25d. Il pedice q indica che è un numero ottale che può essere rappresentato anche dal numero 8; e il pedice d si riferisce al numero decimale, che può anche essere rappresentato dal numero 10.
Conversione da ottale a sistema decimale
Per convertire un numero dal sistema ottale al suo equivalente nel sistema decimale, devi solo moltiplicare ogni cifra ottale per il suo valore di posizione, a partire da destra.
Esempio 1
7328 = (7* 8Due) + (3* 81) + (2* 80) = (7 * 64) + (3 * 8) + (2 * 1)
7328= 448 +24 +2
7328= 47410
Esempio 2
26.98 = (2 *81) + (6* 80) + (9* 8-1) = (2 * 8) + (6 * 1) + (9 * 0,125)
26.98 = 16 + 6 + 1,125
26.98= 23.12510
Conversione da sistema decimale a ottale
Un numero intero decimale può essere convertito in un numero ottale utilizzando il metodo della divisione ripetuta, dove il numero intero decimale viene diviso per 8 finché il quoziente è uguale a 0, e il resto di ogni divisione rappresenterà il numero ottale..
I residui vengono ordinati dall'ultimo al primo; ovvero, il primo resto sarà la cifra meno significativa del numero ottale. In questo modo, la cifra più significativa sarà l'ultimo resto..
Esempio
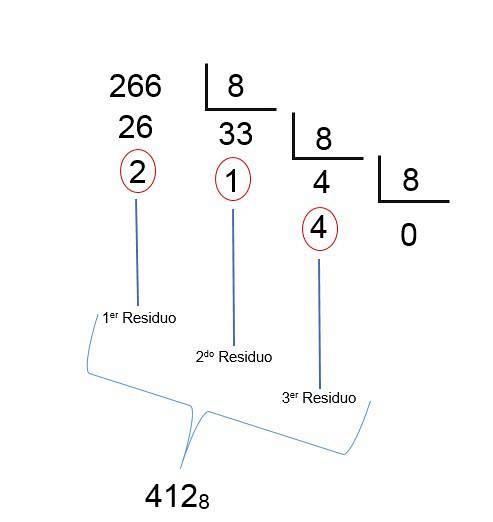
Ottale del numero decimale 26610
- Dividi il numero decimale 266 per 8 = 266/8 = 33 + resto di 2.
- Quindi dividi 33 per 8 = 33/8 = 4 + resto di 1.
- Dividi 4 per 8 = 4/8 = 0 + resto di 4.
Poiché con l'ultima divisione si ottiene un quoziente inferiore a 1, significa che il risultato è stato trovato; Devi solo ordinare i resti inversamente, in modo tale che il numero ottale di 266 decimale sia 412, come si può vedere nell'immagine seguente:
Conversione da ottale a sistema binario
La conversione da ottale a binario viene eseguita convertendo la cifra ottale nella sua cifra binaria equivalente, composta da tre cifre. C'è una tabella che mostra come vengono convertite le otto possibili cifre:
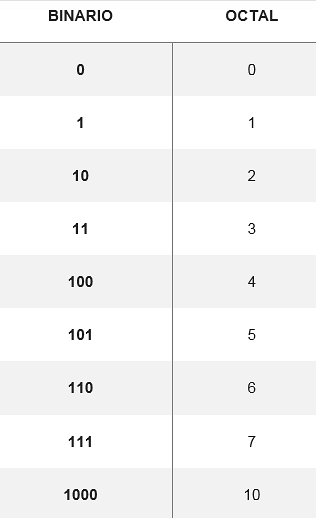
Da queste conversioni puoi cambiare qualsiasi numero dal sistema ottale a binario, ad esempio, per convertire il numero 5728 i loro equivalenti vengono cercati nella tabella. Quindi, deve:
58 = 101
78= 111
Due8 = 10
Pertanto, 5728 è equivalente nel sistema binario a 10111110.
Conversione da binario a ottale
Il processo di conversione di interi binari in interi ottali è l'operazione inversa del processo precedente.
Cioè, i bit del numero binario sono raggruppati in due gruppi di tre bit, a partire da destra a sinistra. Quindi, la conversione da binario a ottale viene eseguita con la tabella precedente.
In alcuni casi il numero binario non avrà gruppi di 3 bit; per completarlo vengono aggiunti uno o due zeri a sinistra del primo gruppo.
Ad esempio, per modificare il numero binario 11010110 in ottale, procedi come segue:
- Si formano gruppi di 3 bit partendo da destra (ultimo bit):
11010110
- Poiché il primo gruppo è incompleto, viene aggiunto uno zero iniziale:
011010110
- La conversione viene effettuata dalla tabella:
011 = 3
010 = 2
110 = 6
Pertanto, il numero binario 011010110 è uguale a 3268.
Conversione da ottale a esadecimale e viceversa
Per passare da un numero ottale al sistema esadecimale o da esadecimale a ottale, è necessario convertire prima il numero in binario e poi nel sistema desiderato.
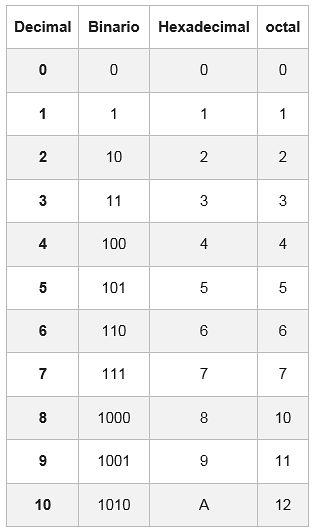
Per questo esiste una tabella dove ogni cifra esadecimale è rappresentata con il suo equivalente nel sistema binario, composta da quattro cifre.
In alcuni casi, il numero binario non avrà gruppi di 4 bit; per completarlo vengono aggiunti uno o due zeri a sinistra del primo gruppo
Esempio
Converti il numero ottale 1646 in un numero esadecimale:
- Converti il numero da ottale a binario
18 = 1
68 = 110
48 = 100
68 = 110
- Così, 16468 = 1110100110.
- Per convertire da binario a esadecimale, vengono prima ordinati in un gruppo di 4 bit, a partire da destra verso sinistra:
11 1010 0110
- Il primo gruppo viene completato con zeri, in modo che possa avere 4 bit:
0011 1010 0110
- La conversione viene eseguita dal sistema binario a quello esadecimale. Le equivalenze vengono sostituite mediante la tabella:
0011 = 3
1010 = A
0110 = 6
Pertanto, il numero ottale 1646 è equivalente a 3A6 nel sistema esadecimale..
Riferimenti
- Bressan, A. E. (1995). Introduzione ai sistemi di numerazione. Argentina University of Business.
- Harris, J. N. (1957). Introduzione ai sistemi di numerazione binaria e ottale: Lexington, Mass. Armed Services Technical Information Agency.
- Kumar, A. A. (2016). Fondamenti di circuiti digitali. Learning Pvt.
- Peris, X. C. (2009). Sistemi operativi singoli.
- Ronald J. Tocci, N. S. (2003). Sistemi digitali: principi e applicazioni. Pearson Education.


Nessun utente ha ancora commentato questo articolo.