Il Reti Bravais Sono l'insieme di quattordici cellule unitarie tridimensionali in cui possono essere localizzati gli atomi di un cristallo. Queste cellule sono costituite da una disposizione tridimensionale di punti che formano una struttura di base che viene ripetuta periodicamente nelle tre direzioni spaziali..
L'origine di questa denominazione per le strutture cristalline di base risale al 1850, quando Auguste Bravais dimostrò che ci sono solo 14 possibili celle tridimensionali unitarie di base.
L'insieme di 14 reti Bravais è suddiviso in sette gruppi o strutture in base alla geometria delle celle, questi sette gruppi sono:
1- Cubico
2- Tetragonale
3- Ortorombica
4- Trigonale-Esagonale
5- Monoclinic
6- Triclinic
7- Trigonale
Ciascuna di queste strutture definisce una cella unitaria, essendo questa la porzione più piccola che preserva la disposizione geometrica degli atomi nel cristallo..
Indice articolo
Le quattordici reti Bravais, come menzionato sopra, sono suddivise in sette gruppi. Ma ognuno di questi gruppi ha le sue celle unitarie con i suoi parametri caratteristici che sono:
1- Il parametro di rete (a, b, c)
2- Numero di atomi per cella
3- Relazione tra parametro di rete e raggio atomico
4- Numero di coordinamento
5- Fattore di imballaggio
6- spazi interstiziali
7- Attraverso traslazioni lungo i vettori a, b, c si ripete la struttura cristallina.
È costituito dalla rete cubica o cubica semplice P, dalla rete cubica centrata sulla faccia o dalla rete cubica F e dalla rete cubica centrata sul corpo o dalla rete cubica I.
Tutte le reti cubiche hanno tutte e tre le reti parametri di rete corrispondenti alle direzioni x, y, z dello stesso valore:
a = b = c
Va notato che gli atomi sono rappresentati da sfere i cui centri sono ai vertici della cella unitaria cubica P.
Nel caso del reticolo cubico P il numero di atomi per cella è 1, perché ad ogni vertice solo un ottavo dell'atomo è all'interno della cella unitaria, quindi 8 * ⅛ = 1.
Il numero di coordinazione indica il numero di atomi vicini nel reticolo cristallino. Nel caso del reticolo cubico P il numero di coordinazione è 6.
In questo tipo di rete, oltre agli atomi ai vertici del cubo, c'è un atomo al centro del cubo. Così il numero di atomi per cella l'unità nel reticolo cubico P è di 2 atomi.
È il reticolo cubico che, oltre agli atomi nei vertici, ha un atomo al centro della faccia di ogni cubo. Il numero di atomi per cella è 4, poiché ciascuno dei sei atomi della faccia ha metà all'interno della cella, ovvero 6 * ½ = 3 più 8 * ⅛ = 1 ai vertici.
In questo caso, la cella unitaria è un prisma dritto con una base esagonale. Le reti esagonali hanno tutti e tre parametri di rete corrispondente adempiendo alla seguente relazione:
a = b ≠ c
L'angolo tra il vettore aeb è di 120º, come mostrato nella figura. Mentre tra i vettori a e c, così come tra bec, si formano angoli retti.
Il numero di atomi per cella sarà calcolato come segue:
- In ciascuna delle 2 basi del prisma esagonale ci sono 6 atomi ai sei vertici. Ciascuno di questi atomi occupa ⅙ della cella unitaria.
- Al centro di ciascuna delle 2 basi esagonali c'è 1 atomo che occupa 1/2 cella unitaria.
- Sulle 6 facce laterali del prisma esagonale ci sono 3 atomi che occupano ciascuno ⅔ della cella unitaria e 3 atomi che occupano ciascuno ⅓ del volume unitario della cella.
(6 x ⅙) x 2 + ½ x 2 + ⅔ x 3 + ⅓ x 3 = 6
La relazione tra i parametri reticolari aeb con il raggio atomico R nell'ipotesi che tutti gli atomi siano di raggio uguale e siano in contatto è:
a / R = b / R = 2
I metalli sono i principali esempi di strutture cristalline e anche i più semplici perché generalmente sono costituiti da un solo tipo di atomo. Ma ci sono altri composti non metallici che formano anche strutture cristalline, come il diamante, il quarzo e molti altri..
Il ferro ha una singola cella unitaria cubica con reticolo o parametro di bordo a = 0,297 nm. In 1 mm ci sono 3,48 x 10 ^ 6 celle unitarie.
Ha una struttura cristallina cubica centrata sulla faccia, composta esclusivamente da atomi di rame..
Le gemme preziose sono strutture cristalline fondamentalmente dello stesso composto, ma con piccole porzioni di impurità che sono spesso responsabili del loro colore..
È composto esclusivamente da carbonio e non contiene impurità, motivo per cui è incolore. Il diamante ha struttura in cristallo cubico (isometrico-esottaedrico) ed è il materiale più duro conosciuto.
È composto da ossido di silice, generalmente è incolore o bianco. La sua struttura cristallina è trigonale-trapezoedrica.
È composto da ossido di alluminio con impurità di cromo che gli conferiscono il caratteristico colore rosso. Forma a reticolo cristallino esagonale.
È anche un cristallo di ossido di alluminio, ma con impurità di titanio e ferro, responsabili del suo colore blu in varie tonalità. Come ha fatto il rubino struttura esagonale.
Gemma generalmente di colore verde, ha struttura monoclina ed è composto da silicato di ferro-magnesio-calcio.
È incolore con a struttura ortorombica fluoruro di alluminio-idrossido-silicato.
Trova la relazione tra il parametro reticolo e il raggio atomico per un reticolo cubico F.
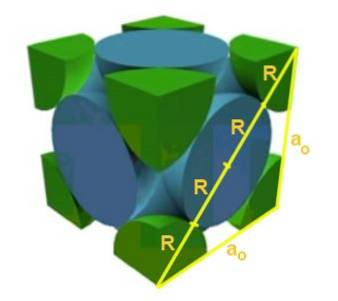
Soluzione: Innanzitutto, si presume che gli atomi siano rappresentati come sfere tutte di raggio R in "contatto" tra loro, come mostrato in figura. Si forma un triangolo rettangolo in cui è vero che:
(4 R) ^ 2 = a ^ 2 + a ^ 2 = 2 a ^ 2
Pertanto, la relazione bordo-raggio è:
a / R = 4 / √2
Trova la relazione tra il parametro reticolo e il raggio atomico per un reticolo cubico I (centrato sul corpo).
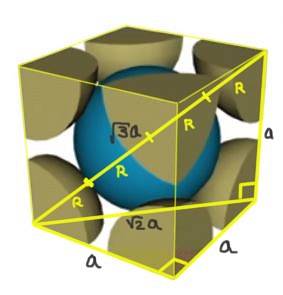
Soluzione: Gli atomi dovrebbero essere rappresentati come sfere tutte di raggio R in "contatto" tra loro, come mostrato in figura.
Si formano due triangoli rettangoli, uno di ipotenusa √2a e l'altro di ipotenusa √3a come si può dimostrare usando il teorema di Pitagora. Da lì ne consegue che la relazione tra il parametro reticolare e il raggio atomico per un reticolo cubico I (centrato nel corpo) è:
a / R = 4 / √3
Trova il fattore di impacchettamento F per una cella unitaria di una struttura cubica F (cubica a facce centrate) in cui gli atomi hanno raggio R e sono in "contatto".
Soluzione: Il fattore di impaccamento F è definito come il quoziente tra il volume occupato dagli atomi nella cella unitaria e il volume della cella:
F = Vatomi / Vcellula
Come dimostrato sopra, il numero di atomi per cella unitaria in un reticolo cubico centrato sulla faccia è 4, quindi il fattore di impacchettamento sarà:
F = 4 [4πR ^ 3/3] / [a ^ 3] = ...
… 4 [4πR ^ 3/3] / [4R / √2] ^ 3 = (√2) π / 6 = 0,74
Nessun utente ha ancora commentato questo articolo.