Cos'è la velocità lineare? (Con esercizi risolti)

Il velocità lineare è definito come ciò che è sempre tangente al percorso seguito dalla particella, indipendentemente dalla sua forma. Se la particella si muove sempre in un percorso rettilineo, non c'è problema a immaginare come il vettore velocità segua questa linea retta.

Tuttavia, in generale il movimento viene eseguito su una curva di forma arbitraria. Ogni porzione della curva può essere modellata come se facesse parte di un cerchio di raggio per, che in ogni punto è tangente al percorso seguito.

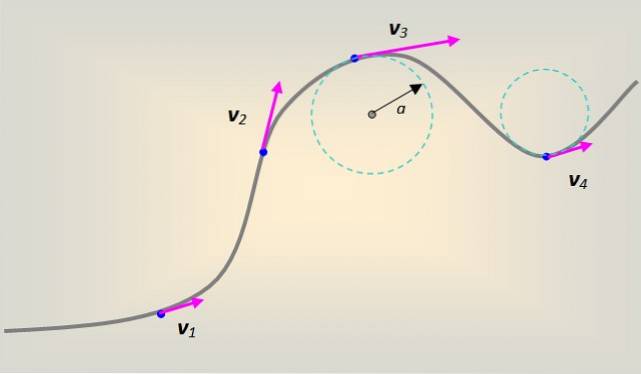
In questo caso, la velocità lineare accompagna la curva tangenzialmente e sempre in ogni punto di essa..

Matematicamente la velocità lineare istantanea è la derivata della posizione rispetto al tempo. Essere r il vettore di posizione della particella in un istante t, quindi la velocità lineare è data dall'espressione:

v = r'(t) = dr / dt

Ciò significa che la velocità lineare o tangenziale, come viene spesso chiamata anche, altro non è che il cambio di posizione rispetto al tempo..

Indice articolo

• 1 Velocità lineare in movimento circolare
  • 1.1 Velocità lineare, velocità angolare e accelerazione centripeta
  • 1.2 -Esercizio risolto 1 
  • 1.3 -Esercizio risolto 2
• 2 Riferimenti

Velocità lineare in movimento circolare

Quando il movimento è su una circonferenza, possiamo andare accanto alla particella in ogni punto e vedere cosa succede in due direzioni molto speciali: una di queste è quella che punta sempre verso il centro. Questo è l'indirizzo radiale.

L'altra direzione importante è quella che passa sulla circonferenza, questa è la direzione tangenziale e la velocità lineare ce l'ha sempre.

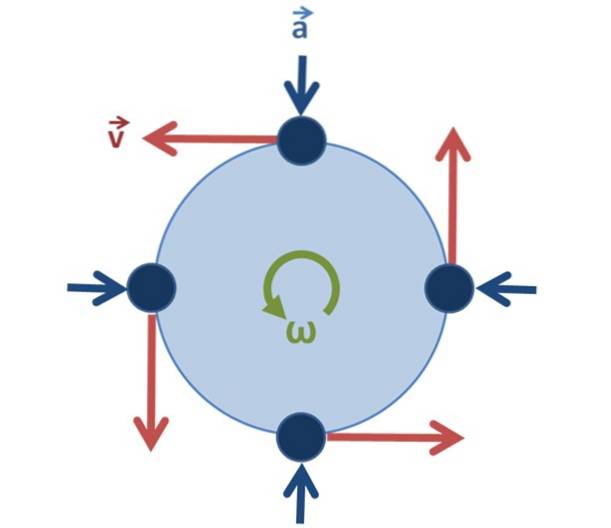
Nel caso di moto circolare uniforme, è importante rendersi conto che la velocità non è costante, poiché il vettore cambia direzione mentre la particella ruota, ma il suo modulo (la dimensione del vettore), che è la velocità, sì rimane invariato.

Per questo movimento la posizione in funzione del tempo è data da s (t), dove S è lui arco eseguito Y t È il momento. In quel caso la velocità istantanea è data dall'espressione v = ds / dt ed è costante.

Se varia anche l'entità della velocità (sappiamo già che la direzione fa sempre, altrimenti il ​​mobile non potrebbe girare), siamo di fronte a un movimento circolare vario, durante il quale il mobile, oltre a girare, può frenare o accelerare.

Velocità lineare, velocità angolare e accelerazione centripeta

Il moto della particella può essere visto anche dal punto di vista del angolo spazzato, invece di farlo dall'arco. In tal caso si parla di velocità angolare. Per un movimento su una circonferenza di raggio R, c'è una relazione tra arco (in radianti) e angolo:

s = R θ

Derivando rispetto al tempo da entrambe le parti:

ds / dt = R (dθ/ dt)

Chiamando la derivata di θ rispetto a t Che cosa velocità angolare e denotandolo con la lettera greca ω "omega", abbiamo questa relazione:

v = ωR

Accelerazione centripeta

Tutto il movimento circolare ha accelerazione centripeta, che è sempre diretto verso il centro della circonferenza. Assicura che la velocità cambi per muoversi con la particella mentre ruota.

Accelerazione centripeta per_c o per_R punta sempre al centro (vedi figura 2) ed è correlato alla velocità lineare in questo modo:

per_c = v^Due / R

E con la velocità angolare come:

per_c = (ωR)^Due / R = ω^DueR

Per un movimento circolare uniforme, la posizione s (t) ha la forma:

s (t) = così + vt

Inoltre, il movimento circolare variato deve avere una componente di accelerazione chiamata accelerazione tangenziale per_T, che si occupa della modifica della grandezza della velocità lineare. sì per_T  è costante, la posizione è:

s (t) = s_o + v_ot + ½ a_Tt^Due

Con v_o come velocità iniziale.

Risolti problemi di velocità lineare

Gli esercizi risolti aiutano a chiarire l'uso corretto dei concetti e delle equazioni sopra riportati..

-Risolto esercizio 1 

Un insetto si muove su un semicerchio di raggio R = 2 m, partendo da fermo nel punto A aumentando la sua velocità lineare, ad una velocità di p m / s^Due. Trova: a) Dopo quanto tempo raggiunge il punto B, b) Il vettore di velocità lineare in quell'istante, c) Il vettore di accelerazione in quell'istante.

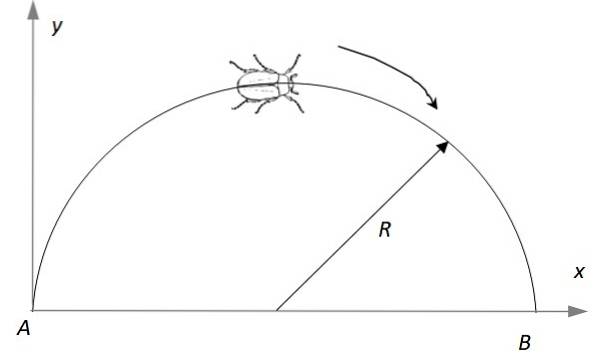
Soluzione

a) L'affermazione indica che l'accelerazione tangenziale è costante ed è uguale a π m / s^Due, allora è valido usare l'equazione per il movimento uniformemente variato:

s (t) = s_o + v_ot + ½ a_T.t^Due

Con s_o = 0 e v_o = 0:

s (t) = ½ a_T.t^Due

s = πR (Metà della lunghezza della circonferenza)

t = (2. πR /per_T) ^½ s = (2π.2 / π)^½s = 2 s

b) v (t) = v_o + per_T. t = 2π SM

Quando nel punto B, il vettore di velocità lineare punta nella direzione verticale verso il basso nella direzione (-Y):

v (t) = 2π SM(-Y)

c) Abbiamo già l'accelerazione tangenziale, manca l'accelerazione centripeta per avere il vettore velocità per:

per_c = v^Due / R = (2π)^Due / 2 m / s^Due = 2π^Due SM^Due

per = a_c (-X) + a_T (-Y) = 2π^Due(-X) + π (-Y) SM^Due

-Esercizio risolto 2

Una particella ruota in un cerchio di raggio 2,90 m. In un particolare istante, la sua accelerazione è di 1,05 m / s^Due in una direzione tale da formare 32º con la sua direzione di movimento. Trova la sua velocità lineare in: a) Questo momento, b) 2 secondi dopo, assumendo che l'accelerazione tangenziale sia costante.

Soluzione

a) La direzione del movimento è precisamente la direzione tangenziale:

per_T = 1,05 m / s^Due . cos 32º = 0,89 m / s^Due ; per_C = 1,05 m / s^Due . sin 32º = 0,56 m / s^Due

La velocità scompare per_c = v^Due / R Che cosa:

v = (R.a_c)^1/2  = 1,27 m / s

b) La seguente equazione è valida per moto variato in modo uniforme: v = v_o + per_Tt = 1,27 + 0,89,2^Due m / s = 4,83 m / s

Riferimenti

1. Bauer, W. 2011. Fisica per l'ingegneria e le scienze. Volume 1. Mc Graw Hill. 84-88.
2. Figueroa, D. Physics Series for Sciences and Engineering. Volume 3 °. Edizione. Cinematica. 199-232.
3. Giancoli, D. 2006. Fisica: principi con applicazioni. 6^th... Ed Prentice Hall. 62-64.
4. Moto relativo. Estratto da: course.lumenlearning.com
5. Wilson, J. 2011. Fisica 10. Pearson Education. 166-168.