
Qual è l'equilibrio della particella? (Con esempi)
Il equilibrio delle particelle È uno stato in cui si trova una particella quando le forze esterne che agiscono su di essa si annullano reciprocamente. Ciò presuppone che mantenga uno stato costante, in modo tale che possa avvenire in due modi differenti a seconda della specifica situazione.
Il primo è essere in equilibrio statico, in cui la particella è immobile; e il secondo è l'equilibrio dinamico, dove la somma delle forze si annulla, ma ciononostante la particella ha moto rettilineo uniforme.

Il modello particellare è un'approssimazione molto utile per studiare il moto di un corpo. Consiste nell'assumere che tutta la massa del corpo sia concentrata in un unico punto, indipendentemente dalle dimensioni dell'oggetto. In questo modo puoi rappresentare un pianeta, un'auto, un elettrone o una palla da biliardo.
Indice articolo
- 1 La forza risultante
- 2 Diagrammi a corpo libero
- 3 modi per applicare la condizione di equilibrio
- 3.1 Due forze di uguale grandezza e direzione e direzioni opposte
- 3.2 Due forze di diversa grandezza, stessa direzione e direzioni opposte
- 3.3 Due forze di uguale grandezza e direzione diversa
- 3.4 Tre forze con direzione diversa
- 4 attrito
- 4.1 L'attrito dinamico
- 5 Esempio lavorato
- 5.1 Soluzione
- 6 Riferimenti
La forza risultante
Il punto che rappresenta l'oggetto è dove agiscono le forze che lo influenzano. Tutte queste forze possono essere sostituite da una sola che fa lo stesso effetto, che viene chiamato forza risultante o forza netta ed è indicato come FR o FN.
Secondo la seconda legge di Newton, quando c'è una forza risultante sbilanciata, il corpo subisce un'accelerazione proporzionale alla forza:
FR = m.a
Dove per è l'accelerazione che l'oggetto acquisisce grazie all'azione della forza e m è la massa dell'oggetto. Cosa succede se il corpo non viene accelerato? Proprio quanto indicato all'inizio: il corpo è a riposo o si muove con moto rettilineo uniforme, che manca di accelerazione.
Per una particella in equilibrio è valido assicurarsi che:
FR = 0
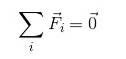
Poiché l'aggiunta di vettori non implica necessariamente l'aggiunta di moduli, i vettori devono essere scomposti. Pertanto, è valido esprimere:
FX = m.aX = 0; FY = m.aY = 0; Fz = m.az = 0
Diagrammi a corpo libero
Per visualizzare le forze che agiscono sulla particella, è conveniente realizzare un diagramma a corpo libero, in cui tutte le forze che agiscono sull'oggetto sono rappresentate da frecce..
Le equazioni di cui sopra sono di natura vettoriale. Quando si decompongono le forze, si distinguono per segni. In questo modo è possibile che la somma delle sue componenti sia zero.
Le seguenti sono linee guida importanti per rendere utile il disegno:
- Scegli un sistema di riferimento in cui la maggior quantità di forze si trova sugli assi delle coordinate.
- Il peso è sempre disegnato verticalmente verso il basso.
- Nel caso di due o più superfici a contatto, esistono forze normali, che vengono sempre disegnate spingendo il corpo e perpendicolari alla superficie che lo esercita..
- Per una particella in equilibrio possono esserci degli attriti paralleli alla superficie di contatto e opposti al possibile movimento, se la particella è considerata a riposo, o decisamente in opposizione, se la particella si muove con MRU (movimento rettilineo uniforme).
- Se c'è una corda, la tensione viene sempre tirata lungo di essa e tira il corpo.
Modi per applicare la condizione di equilibrio
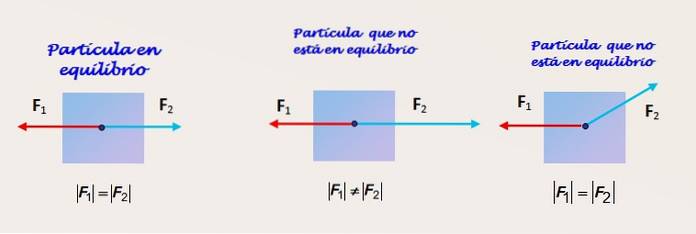
Due forze di uguale grandezza e direzione e direzioni opposte
La figura 2 mostra una particella su cui agiscono due forze. Nella figura a sinistra la particella riceve l'azione di due forze F1 e FDue che hanno la stessa grandezza e agiscono nella stessa direzione e in direzioni opposte.
La particella è in equilibrio, ma nonostante le informazioni fornite non è possibile sapere se l'equilibrio è statico o dinamico. Sono necessarie ulteriori informazioni sul sistema di riferimento inerziale da cui si osserva l'oggetto.
Due forze di diversa grandezza, stessa direzione e direzioni opposte
La figura al centro mostra la stessa particella, che questa volta non è in equilibrio, poiché l'entità della forza FDue è maggiore di quella di F1. Quindi c'è una forza sbilanciata e l'oggetto ha un'accelerazione nella stessa direzione di FDue.
Due forze di uguale grandezza e direzione diversa
Infine, nella figura a destra vediamo un corpo che non è neppure in equilibrio. Nonostante il fatto che F1 e FDue hanno uguale grandezza, la forza FDue non è nella stessa direzione di 1. La componente verticale di FDue non viene contrastato da nessun altro e la particella subisce un'accelerazione in quella direzione.
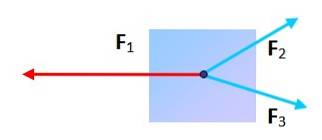
Tre forze con direzione diversa
Può una particella soggetta a tre forze essere in equilibrio? Sì, fintanto che quando si posiziona la fine e la fine di ciascuna, la figura risultante è un triangolo. In questo caso la somma dei vettori è zero.
Attrito
Una forza che interviene frequentemente nell'equilibrio della particella è l'attrito statico. È dovuto all'interazione dell'oggetto rappresentato dalla particella con la superficie di un altro. Ad esempio, un libro in equilibrio statico su un tavolo inclinato è modellato come una particella e ha un diagramma a corpo libero come il seguente:
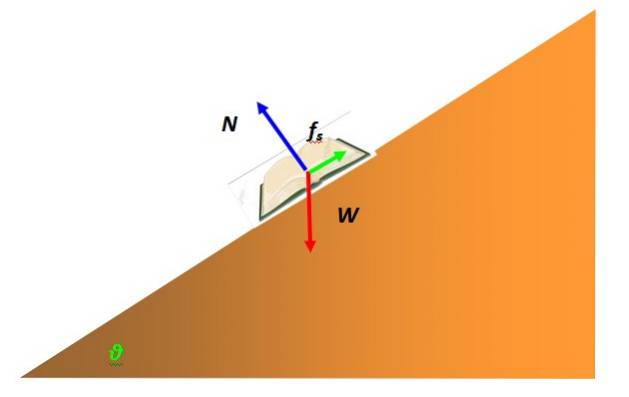
La forza che impedisce al libro di scivolare sulla superficie del piano inclinato e rimanere a riposo è l'attrito statico. Dipende dalla natura delle superfici a contatto, che microscopicamente presentano rugosità con picchi che si incastrano tra loro rendendo difficile il movimento..
Il valore massimo di attrito statico è proporzionale alla forza normale, la forza esercitata dalla superficie sull'oggetto supportato, ma perpendicolare a detta superficie. Nell'esempio del libro è indicato in blu. Matematicamente si esprime così:
Fs di più∝ N
La costante di proporzionalità è il coefficiente di attrito statico μS, che è determinato sperimentalmente, è adimensionale e dipende dalla natura delle superfici a contatto.
Fs max = μS N
L'attrito dinamico
Se una particella è in equilibrio dinamico, il movimento ha già luogo e l'attrito statico non interviene più. Se è presente una forza di attrito che si oppone al movimento, interviene l'attrito dinamico, la cui entità è costante ed è data da:
FK = μK N
Dove μK è lui coefficiente di attrito dinamico, Dipende anche dal tipo di superfici a contatto. Come il coefficiente di attrito statico, è adimensionale e il suo valore è determinato sperimentalmente.
Il valore del coefficiente di attrito dinamico è solitamente inferiore a quello dell'attrito statico.
Esempio funzionante
Il libro nella figura 3 è a riposo e ha una massa di 1,30 kg. L'aereo ha un angolo di inclinazione di 30º. Trova il coefficiente di attrito statico tra il libro e la superficie piana.
Soluzione
È importante selezionare un sistema di riferimento adatto, vedere la figura seguente:
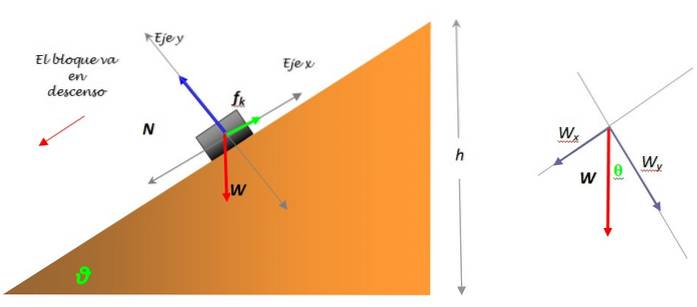
Il peso del libro ha grandezza W = mg, tuttavia è necessario scomporlo in due componenti: WX Y WY, poiché è l'unica forza che non cade appena sopra nessuno degli assi delle coordinate. La scomposizione del peso si osserva nella figura a sinistra.
WY = mg.cosθ = 1,30 x 9,8 x cos 30º N = 11,03 N
WX = mg sinθ = 1,30 x 9,8 x seno 30º = 6,37 N
Il 2 °. La legge di Newton per l'asse verticale è:
N - Wy = 0
N = mg. cos θ = 11,03 N.
Applicando il 2 °. Legge di Newton per l'asse x, scegliendo come positiva la direzione del movimento possibile:
WX - FS = 0
L'attrito massimo è FS max= μSN, Quindi:
WX - μSN = 0
μS = WX / N = 6,37 / 11,03 = 0,58
Riferimenti
- Rex, A. 2011. Fondamenti di fisica. Pearson. 76 - 90.
- Serway, R., Jewett, J. (2008). Fisica per la scienza e l'ingegneria. Volume 1. 7ma. Ed. Cengage Learning. 120-124.
- Serway, R., Vulle, C. 2011. Fondamenti di fisica. 9n / A Ed. Cengage Learning. 99-112.
- Tippens, P. 2011. Fisica: concetti e applicazioni. 7a edizione. MacGraw Hill. 71 - 87.
- Walker, J. 2010. Fisica. Addison Wesley. 148-164.



Nessun utente ha ancora commentato questo articolo.