
Equazione dei punti complanari, esempio ed esercizi risolti
Il punti complanari appartengono tutti allo stesso piano. Due punti sono sempre complanari, poiché questi punti definiscono una linea attraverso la quale passano piani infiniti. Quindi, entrambi i punti appartengono a ciascuno dei piani che passano attraverso la linea e quindi saranno sempre complanari.
D'altra parte, tre punti definiscono un unico piano, da cui segue che tre punti saranno sempre complanari al piano che determinano..
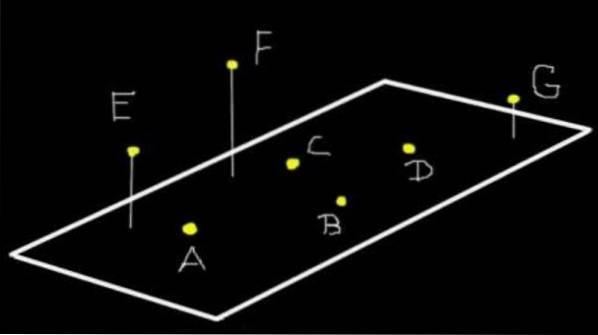
Più di tre punti possono essere complanari o meno. Ad esempio, nella Figura 1, i punti A, B, C e D sono complanari al piano (Ω). Ma E, F e G non sono complanari a (Ω), sebbene siano complanari al piano che definiscono.
Indice articolo
- 1 Equazione di un piano dato tre punti
- 2 Esempio
- 2.1 Soluzione
- 3 esercizi risolti
- 3.1 - Esercizio 1
- 3.2 - Esercizio 2
- 3.3 - Esercizio 3
- 3.4 - Esercizio 4
- 4 Riferimenti
Equazione di un piano dato tre punti
L'equazione di un piano determinata da tre punti noti A, B, C è una relazione matematica che garantisce che qualsiasi punto P con coordinate generiche (x, y, z) che soddisfi l'equazione appartenga a detto piano.
L'affermazione precedente equivale a dire che se P di coordinate (x, y, z) soddisfa l'equazione del piano, allora detto punto sarà complanare con i tre punti A, B, C che hanno determinato il piano.
Per trovare l'equazione di questo piano, iniziamo trovando i vettori AB Y AC:
AB = [Bx - Ax, By - Ay, Bz - Az]
AC = [Cx - Ax, Cy - Ay, Cz - Az]
Il prodotto vettoriale AB X AC risulta in un vettore perpendicolare o normale al piano determinato dai punti A, B, C.
Qualsiasi punto P di coordinate (x, y, z) appartiene al piano se il vettore AP è perpendicolare al vettore AB X AC, che è garantito se:
AP • (AB X AC) = 0
Ciò equivale a dire che il triplo prodotto di AP, AB Y AC è zero. L'equazione di cui sopra può essere scritta in forma di matrice:
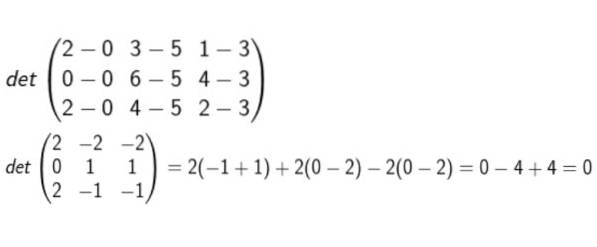
Esempio
Siano i punti A (0, 1, 2); B (1, 2, 3); C (7, 2, 1) e D (per, 0, 1). Che valore dovrebbe avere per in modo che i quattro punti siano complanari?
Soluzione
Per trovare il valore di a, il punto D deve essere parte del piano determinato da A, B e C, che è garantito se soddisfa l'equazione del piano.
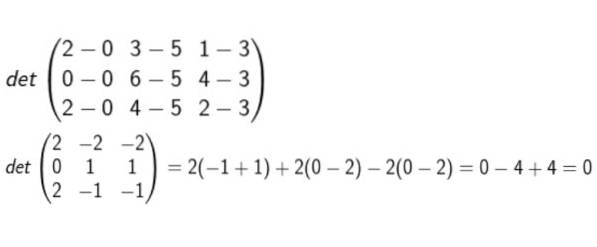
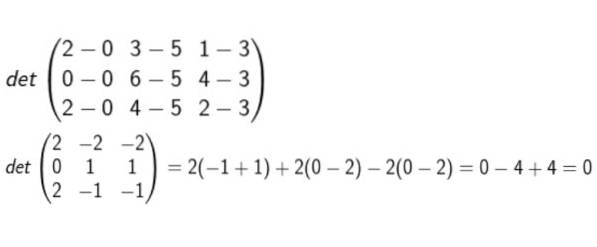
Sviluppando il determinante abbiamo:
a (-1-1) + 1 (-1 - 7) -1 (1 - 7) = -2a -8 + 6 = -2a - 2 = 0
L'equazione di cui sopra ce lo dice a = -1 in modo che l'uguaglianza sia soddisfatta. In altre parole, l'unico modo in cui il punto D (per, 0,1) è complanare con i punti A, B e C è quello per vale -1. Altrimenti non sarà complanare.
Esercizi risolti
- Esercizio 1
Un piano interseca gli assi cartesiani X, Y, Z rispettivamente in 1, 2 e 3. L'intersezione di questo piano con gli assi determina i punti A, B e C.Trova la componente Dz di un punto D, le cui componenti cartesiane sono:
D (-Dz, Dz + 1, Dz)
A condizione che D sia complanare con i punti A, B e C.
Soluzione
Quando sono note le intercette di un piano con assi cartesiani, si può utilizzare la forma segmentale dell'equazione del piano:
x / 1 + y / 2 + z / 3 = 1
Poiché il punto D deve appartenere al piano precedente, deve:
-Dz / 1 + (Dz + 1) / 2 + Dz / 3 = 1
Vale a dire:
-Dz + Dz / 2 + ½ + Dz / 3 = 1
Dz (-1 + ½ + ⅓) = ½
Dz (-1 / 6⅙) = ½
Dz = -3
Da quanto sopra segue che il punto D (3, -2, -3) è complanare ai punti A (1, 0, 0); B (0, 2, 0) e C (0, 0, 3).
- Esercizio 2
Determina se i punti A (0, 5, 3); B (0, 6, 4); C (2, 4, 2) e D (2, 3, 1) sono complanari.
Soluzione
Formiamo la matrice le cui righe sono le coordinate di D-A, B-A e C-A. Quindi viene calcolato il determinante e viene verificato se è zero o meno.
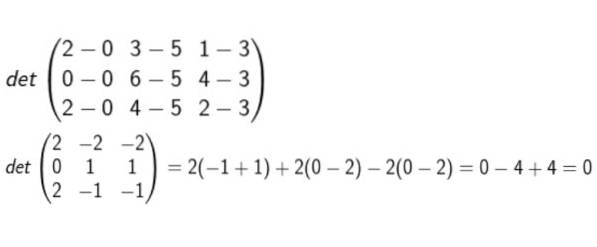
Dopo aver eseguito tutti i calcoli, si conclude che sono complanari.
- Esercizio 3
Ci sono due linee nello spazio. Uno di questi è la retta (R) la cui equazione parametrica è:
(R): x = 1 + 2 λ; y = 1 - λ; z = 1
E l'altra è la retta (S) la cui equazione è:
(S): x + 2 y = 1; z = -1
Mostra che (R) e (S) sono linee complanari, cioè giacciono sullo stesso piano.
Soluzione
Iniziamo prendendo arbitrariamente due punti sulla linea (R) e due sulla linea (S):
Dritto (R): λ = 0; A (1, 1, 1) e λ = 1; B (3, 0, 1)
Facciamo x = 0 sulla linea (S)=> y = ½; C (0, ½, -1). E d'altra parte, se lo facciamo y = 0 => x = 1; D (1, 0, -1).
Cioè, abbiamo preso i punti A e B che appartengono alla linea (R) e i punti C e D che appartengono alla linea (S). Se questi punti sono complanari, anche le due linee saranno complanari.
Ora scegliamo il punto A come perno e poi troviamo le coordinate dei vettori AB, AC Y ANNO DOMINI. In questo modo ottieni:
B - A: (3-1, 0-1, 1-1) => AB= (2, -1, 0)
DO - LA: (0-1, 1/2 -1, -1 - 1) => AC= (-1, -1/2, -2)
RE - LA: (1-1, 0-1, -1 - 1) => ANNO DOMINI= (0, -1, -2)
Il passaggio successivo consiste nel costruire e calcolare il determinante la cui prima riga sono i coefficienti del vettore AB, la seconda riga sono quelle di AC e la terza riga quelli del vettore ANNO DOMINI:
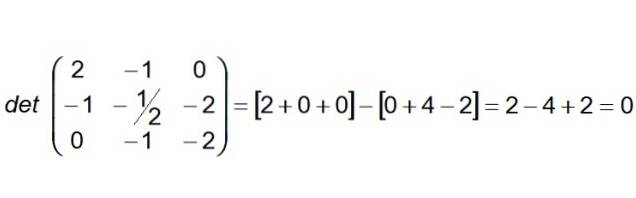
Poiché il determinante risulta essere nullo, possiamo concludere che i quattro punti sono complanari. Inoltre si può affermare che anche le linee (R) e (S) sono complanari.
- Esercizio 4
Le rette (R) e (S) sono complanari, come dimostrato nell'esercizio 3. Trova l'equazione del piano che le contiene.
Soluzione
I punti A, B, C definiscono completamente quel piano, ma vogliamo imporre che qualsiasi punto X di coordinate (x, y, z) appartenga allo stesso.
X - A: (x-1, y -1, z - 1) => ASCIA= (x-1, y -1, z - 1)
B - A: (3-1, 0-1, 1-1) => AB= (2, -1, 0)
DO - LA: (0-1, 1/2 -1, -1 - 1) => AC= (-1, -1/2, -2)
Affinché X appartenga al piano definito da A, B, C e in cui sono contenute le rette (R) e (S), è necessario che il determinante formato nella sua prima riga dai componenti di ASCIA, nel secondo da quelli di AB e nel terzo da quelli di AC:
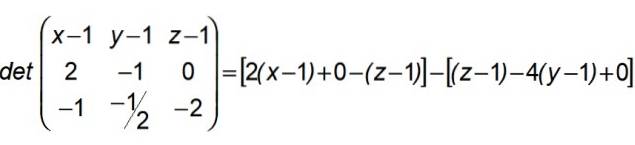
A seguito di questo risultato, raggruppiamo in questo modo:
2 (x-1) + 4 (y-1) -2 (z-1) = 0
E subito vedi che può essere riscritto così:
x - 1 + 2y - 2 - z + 1 = 0
Quindi x + 2y - z = 2 è l'equazione del piano che contiene le rette (R) e (S).
Riferimenti
- Fleming, W. 1989. Precalculus Mathematics. Prentice Hall PTR.
- Kolman, B. 2006. Algebra lineare. Pearson Education.
- Leal, J. M. 2005. Geometria analitica piana. Mérida - Venezuela: Editoriale Venezolana C. A.
- Navarro, Rocio. Vettori. Estratto da: books.google.co.ve.
- Pérez, C. D. 2006. Pre-calcolo. Pearson Education.
- Prenowitz, W. 2012. Concetti di base della geometria. Rowman e Littlefield.
- Sullivan, M. 1997. Precalculus. Pearson Education.



Nessun utente ha ancora commentato questo articolo.