
Spiegazione della proporzionalità composta, regola del tre composta, esercizi
Il proporzionalità composta o multipla È la relazione tra più di due grandezze, dove si può osservare la proporzionalità diretta e inversa tra i dati e l'ignoto. Questa è una versione più avanzata della semplice proporzionalità, sebbene le tecniche utilizzate in entrambe le procedure siano simili..
Ad esempio, se sono necessarie 7 persone per scaricare 10 tonnellate di merce in 3 ore, è possibile utilizzare la proporzionalità composta per calcolare quante persone saranno necessarie per scaricare 15 tonnellate in 4 ore..
Per rispondere a questa domanda, è conveniente fare una tabella di valori per studiare e mettere in relazione le grandezze e le incognite.
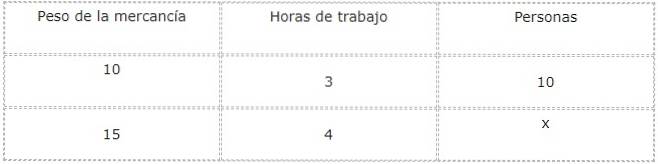
Procediamo ad analizzare i tipi di relazioni tra ogni grandezza e il presente sconosciuto, che per questo caso corrisponde al numero di persone che lavoreranno.
Con l'aumentare del peso della merce, aumenta anche il numero di persone necessarie per scaricarla. Per questo motivo, il rapporto tra peso e lavoratori è diretto.
D'altra parte, all'aumentare del numero di lavoratori, l'orario di lavoro diminuisce. Per questo il rapporto tra persone e ore di lavoro è di tipo inverso.
Indice articolo
- 1 Come calcolare le proporzionalità composte
- 2 Spiegazione
- 3 Regola diretta del tre
- 4 Regola inversa del tre
- 5 Condizione
- 6 Verifica dei risultati
- 7 Liquidazione
- 8 Storia
- 9 Esercizi risolti
- 9.1 Esercizio 1
- 9.2 Esercizio 2
- 10 Esercizi proposti
- 11 Riferimenti
Come calcolare le proporzionalità composte
Per risolvere esempi come quello sopra, viene utilizzata principalmente la regola composta del metodo dei tre. Consiste nello stabilire i tipi di relazioni tra grandezze e incognite e quindi rappresentare un prodotto tra le frazioni.
Rispetto all'esempio iniziale, le frazioni corrispondenti alla tabella dei valori sono organizzate come segue:
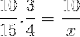
Ma prima di risolvere e risolvere l'ignoto, le frazioni corrispondenti alla relazione inversa devono essere invertite. Che in questo caso corrispondono alla variabile tempo. In questo modo l'operazione da risolvere sarà:
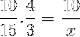
La cui unica differenza è l'inversione della frazione corrispondente alla variabile temporale 4/3. Procediamo per operare e azzerare il valore di x.
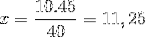
Pertanto, sono necessarie più di undici persone per poter scaricare 15 tonnellate di merce in 4 ore o meno.
Spiegazione
La proporzionalità è la relazione costante tra le quantità soggette a cambiamento, che sarà simmetrica per ciascuna delle quantità coinvolte. Esistono relazioni direttamente e inversamente proporzionali, definendo così i parametri di proporzionalità semplice o composta.
Regola diretta del tre
Consiste in una relazione di proporzione tra variabili, che mostrano lo stesso comportamento quando vengono modificate. È molto frequente nel calcolo di percentuali riferite a grandezze diverse da cento, dove si apprezza la sua struttura fondamentale.
A titolo di esempio si può calcolare il 15% di 63. A prima vista, questa percentuale non è facilmente apprezzabile. Ma implementando la regola del tre, è possibile stabilire la seguente relazione: se 100% è 63, quindi 15%, quanto sarà?
100% - 63
15% -X
E l'operazione corrispondente è:
(15%. 63) / 100% = 9,45
Dove si semplificano i segni di percentuale e si ottiene la cifra 9.45, che rappresenta il 15% di 63.
Regola inversa del tre
Come indica il nome, in questo caso la relazione tra le variabili è opposta. La relazione inversa deve essere stabilita prima di procedere al calcolo. La sua procedura è omologa a quella della regola diretta del tre, salvo l'investimento nella frazione da calcolare..
Ad esempio, 3 pittori hanno bisogno di 5 ore per finire un muro. In quante ore lo finirebbero 4 pittori?
In questo caso il rapporto è inverso, poiché all'aumentare del numero dei pittori, il tempo di lavoro dovrebbe diminuire. La relazione è stabilita;
3 pittori - 5 ore
4 pittori- X ore
Quando la relazione viene invertita, l'ordine delle operazioni viene invertito. Questo è il modo corretto;
(3 pittori). (5 ore) / 4 imbianchini = 3,75 ore
Il termine pittori è semplificato e il risultato è di 3,75 ore.
Condizione
Per essere in presenza di una proporzionalità composta o multipla, è necessario trovare entrambi i tipi di relazione tra le grandezze e le variabili.
- Diretto: la variabile ha lo stesso comportamento dell'ignoto. Cioè, quando uno aumenta o diminuisce, l'altro si altera allo stesso modo.
- Inverso: la variabile presenta un comportamento contrario a quello dell'ignoto. La frazione che definisce detta variabile nella tabella dei valori deve essere invertita, per rappresentare la relazione inversamente proporzionale tra variabile e incognita..
Verifica dei risultati
È molto comune confondere l'ordine delle grandezze quando si lavora con proporzionalità composte, a differenza di quanto avviene nei soliti calcoli delle proporzioni, la cui natura è per lo più diretta e risolvibile per mezzo di una semplice regola del tre..
Per questo motivo è importante esaminare l'ordine logico dei risultati, verificando la coerenza delle cifre prodotte dalla regola del tre composto.
Nell'esempio iniziale, commettere un errore del genere porterebbe a 20 come risultato. Ovvero 20 persone per scaricare 15 tonnellate di merce in 4 ore.
A prima vista non sembra un risultato folle, ma è curioso un aumento di quasi il 200% del personale (da 7 a 20 persone) quando l'aumento della merce è del 50%, e anche con un maggiore margine di tempo per eseguire il lavoro.
In questo modo, la verifica logica dei risultati rappresenta un passaggio importante nell'attuazione della regola dei tre composti..
Liquidazione
Sebbene di natura più elementare rispetto alla formazione matematica, l'autorizzazione rappresenta un passo importante nei casi di proporzionalità. Un nulla osta sbagliato è sufficiente per invalidare qualsiasi risultato ottenuto con la regola del tre semplice o composta..
Storia
La regola dei tre divenne nota in Occidente attraverso gli arabi, con pubblicazioni di vari autori. Tra loro Al-Jwarizmi e Al-Biruni.
Al-Biruni, grazie alla sua conoscenza multiculturale, ha avuto accesso a vaste informazioni riguardo a questa pratica nei suoi viaggi in India, essendo responsabile della più ampia documentazione sulla regola del tre.
Nella sua ricerca sostiene che l'India è stato il primo luogo in cui l'uso della regola del tre è diventato comune. Lo scrittore assicura che è stato eseguito in modo fluido nelle sue versioni dirette, inverse e anche composte..
La data esatta in cui la regola dei tre è entrata a far parte della conoscenza matematica dell'India è ancora sconosciuta. Tuttavia, il documento più antico che affronta questa pratica, il manoscritto Bakhshali, fu scoperto nel 1881. Attualmente si trova a Oxford.
Molti storici della matematica affermano che questo manoscritto risale all'inizio dell'era attuale..
Esercizi risolti
Esercizio 1
Una compagnia aerea deve trasportare 1.535 persone. È noto che con 3 aerei ci vorrebbero 12 giorni per portare a destinazione l'ultimo passeggero. Altre 450 persone sono arrivate alla compagnia aerea e 2 aerei devono essere riparati per aiutare in questo compito. Quanti giorni impiegherà la compagnia aerea per trasferire l'ultimo passeggero a destinazione?
Il rapporto tra il numero di persone e le giornate di lavoro è diretto, perché maggiore è il numero di persone, più giorni ci vorranno per svolgere questo lavoro..
D'altra parte, il rapporto tra aeroplani e giorni è inversamente proporzionale. Con l'aumentare del numero di aerei, i giorni necessari per trasferire tutti i passeggeri diminuiscono.
Viene realizzata la tabella dei valori riferiti a questo caso.

Come dettagliato nell'esempio iniziale, il numeratore e il denominatore devono essere invertiti nella frazione corrispondente alla variabile inversa rispetto all'ignoto. L'operazione è la seguente:
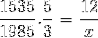
X = 71460/7675 = 9,31 giorni
Per trasferire 1985 persone che utilizzano 5 aerei, ci vogliono più di 9 giorni.
Esercizio 2
Un raccolto di mais da 25 tonnellate viene portato ai camion del carico. Si sa che l'anno precedente ci sono volute 8 ore con un libro paga di 150 lavoratori. Se per quest'anno il libro paga è aumentato del 35%, quanto tempo ci vorrà per riempire i camion con un raccolto di 40 tonnellate??
Prima di rappresentare la tabella dei valori, è necessario definire il numero di lavoratori per quest'anno. Questo è aumentato del 35% rispetto alla cifra iniziale di 150 lavoratori. Per questo viene utilizzata una regola diretta del tre.
100% - 150
35% - X
X = (35.100) / 100 = 52,5. E 'il numero di addetti in più rispetto all'anno precedente, ottenendo un numero totale di lavoratori di 203, dopo aver arrotondato l'importo ottenuto.
Si procede alla definizione della tabella dati corrispondente

In questo caso, il peso rappresenta una variabile direttamente correlata al tempo sconosciuto. D'altra parte, la variabile worker ha una relazione inversa con il tempo. Maggiore è il numero di lavoratori, minore è la giornata lavorativa.
Tenendo conto di queste considerazioni e invertendo la frazione corrispondente alla variabile worker, procediamo al calcolo.
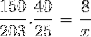
X = 40600/6000 = 6,76 ore
La giornata richiederà poco meno di 7 ore.
Esercizi proposti
- Definisci il 73% di 2875.
- Calcola il numero di ore che Teresa dorme, se si sa che dorme solo il 7% del totale della giornata. Definisci quante ore dormi a settimana.
- Un giornale pubblica 2000 copie ogni 5 ore, utilizzando solo 2 macchine da stampa. Quante copie produrrà in 1 ora, se usa 7 macchine? Quanto tempo ci vorranno 10.000 copie utilizzando 4 macchine?
Riferimenti
- Enciclopedia Alvarez-iniziazione. A. Álvarez, Antonio Álvarez Pérez. EDAF, 2001.
- Manuale completo di istruzione elementare e primaria superiore: ad uso di aspiranti insegnanti e soprattutto studenti delle scuole normali della provincia, volume 1. Joaquín Avendaño. Stampa di D.Dionisio Hidalgo, 1844.
- Approssimazione razionale delle funzioni reali. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3 marzo. 2011.
- Aritmetica elementare per l'insegnamento nelle scuole e nei college dell'America centrale. Darío González. Mancia. Arenales, 1926.
- Lo studio della matematica: sullo studio e le difficoltà della matematica. Augustus De Morgan. Baldwin e Cradock, 1830.


Nessun utente ha ancora commentato questo articolo.