
Programmazione lineare a cosa serve, modelli, vincoli, applicazioni
Il programmazione lineare è un metodo matematico utilizzato per ottimizzare (massimizzare o ridurre al minimo secondo necessità) una funzione le cui variabili sono soggette a restrizioni, purché la funzione e le restrizioni siano linearmente dipendenti dalle variabili.
In generale, la funzione da ottimizzare modella una situazione pratica, come il profitto di un produttore i cui input, manodopera o macchinari sono limitati.

Uno dei casi più semplici è quello di una funzione lineare da massimizzare, che dipende solo da due variabili, chiamate variabili decisionali. Può essere della forma:
Z = k1x + kDueY
Con k1 e kDue costante. Questa funzione è nota come Funzione obiettivo. Certo, ci sono situazioni che meritano più di due variabili per lo studio, essendo più complesse:
Z = k1X1 + KDueXDue + K3X3 +... .
E i vincoli sono anche modellati matematicamente da un sistema di equazioni o disequazioni, ugualmente lineari in X e Y.
Viene chiamato l'insieme di soluzioni di questo sistema soluzioni fattibili o punti fattibili. E tra i punti fattibili ce n'è almeno uno, che ottimizza la funzione obiettivo.
La programmazione lineare è stata sviluppata in modo indipendente dal fisico e matematico americano George Dantzig (1914-2005) e dal matematico ed economista russo Leonid Kantorovich (1912-1986) poco dopo la seconda guerra mondiale..
Il metodo di risoluzione dei problemi noto come metodo simplex Nasce da un'idea di Dantzig, che ha lavorato per la US Air Force, l'Università di Berkeley e la Stanford University.

Indice articolo
- 1 Modelli di programmazione lineare
- 2 Esempio di modello
- 3 Metodi di soluzione
- 3.1 - Metodo grafico o geometrico
- 3.2 - Metodo simplex di Dantzig
- 4 Applicazioni
- 5 Esercizi risolti
- 5.1 - Esercizio 1
- 5.2 - Esercizio 2
- 6 Riferimenti
Modelli di programmazione lineare
Gli elementi necessari per stabilire un modello di programmazione lineare, adatto ad una situazione pratica, sono:
-Funzione obiettivo
-Variabili decisionali
-Restrizioni
Nella funzione obiettivo definisci cosa vuoi ottenere. Ad esempio, supponi di voler massimizzare i tuoi profitti dalla fabbricazione di determinati prodotti. Quindi viene stabilita la funzione "profitto", in base al prezzo al quale i prodotti vengono venduti.
In termini matematici, questa funzione può essere espressa abbreviata utilizzando la notazione di sommatoria:
Z = ∑kio Xio
In questa equazione, kio sono coefficienti e xio sono le variabili decisionali.
Le variabili decisionali sono gli elementi del sistema di cui si ha il controllo ei loro valori sono numeri reali positivi. Nell'esempio proposto, le variabili decisionali sono la quantità di ogni prodotto da realizzare per ottenere il massimo profitto.
Infine, abbiamo i vincoli, che sono equazioni lineari o disequazioni in termini di variabili di decisione. Descrivono le limitazioni al problema, che sono note e possono essere, ad esempio, le quantità di materia prima disponibile nella produzione..
Tipi di restrizioni
Puoi avere un numero M di limitazioni, a partire da j = 1 fino a j = M. Matematicamente le restrizioni sono di tre tipi:
- PERj = ∑ aij . Xio
- Bj ≥ ∑ bij . Xio
- Cj ≤ ∑ cij . Xio
La prima restrizione è del tipo di equazione lineare e significa che il valore Aj, che è noto, deve essere rispettato.
I restanti due vincoli sono disuguaglianze lineari e significa che i valori B.j e Cj, noti, possono essere rispettati o superati, quando il simbolo visualizzato è ≥ (maggiore o uguale a) oppure rispettati o non superati, se il simbolo è ≤ (minore o uguale a).
Esempio di modello
I campi di applicazione sono molto diversi, spaziano dall'amministrazione aziendale all'alimentazione, ma per comprendere il metodo si propone di seguito un semplice modello di una situazione pratica con due variabili..
Una pasticceria locale è nota per due specialità: la torta della foresta nera e la torta sacripantina..
Nella sua preparazione richiedono uova e zucchero. Per la foresta nera servono 9 uova e 500 g di zucchero, mentre per la sacripantine servono 8 uova e 800 g di zucchero. I rispettivi prezzi di vendita sono $ 8 e $ 10.
Il problema è: quante torte di ogni tipo deve fare la pasticceria per massimizzare il suo profitto, sapendo che ha 10 chili di zucchero e 144 uova?
Variabili decisionali
Le variabili decisionali sono "x" e "y", che assumono valori reali:
-x: il numero di torte della foresta nera
-e: le torte tipo sacripantina.
Restrizioni
Le restrizioni sono date dal fatto che il numero di torte è un quantitativo positivo e ci sono limitate quantità di materia prima per prepararle..
Pertanto, in forma matematica, queste restrizioni assumono la forma:
- x ≥ 0
- e ≥0
- 9x + 8y ≤ 144
- 0,5 x + 0,8y ≤ 10
I vincoli 1 e 2 costituiscono il condizione di non negatività esposto in precedenza, e tutte le disuguaglianze sollevate sono lineari. Nelle restrizioni 3 e 4 ci sono i valori che non devono essere superati: 144 uova e 10 kg di zucchero.
Funzione obiettivo
Infine, la funzione obiettivo è il profitto ottenuto producendo la quantità "x" di torte della foresta nera più la quantità "y" di sacripantine. È costruito moltiplicando il prezzo per la quantità di torte fatte e aggiungendo per ogni tipo. È una funzione lineare che chiameremo G (x, y):
G = 8x + 10y
Metodi di soluzione
Le varie metodologie di soluzione includono metodi grafici, l'algoritmo simplex e il metodo del punto interno, per citarne alcuni..
- Metodo grafico o geometrico
Quando hai un problema a due variabili come quello nella sezione precedente, i vincoli determinano una regione poligonale nel piano xy, chiamata regione fattibile o regione di redditività.
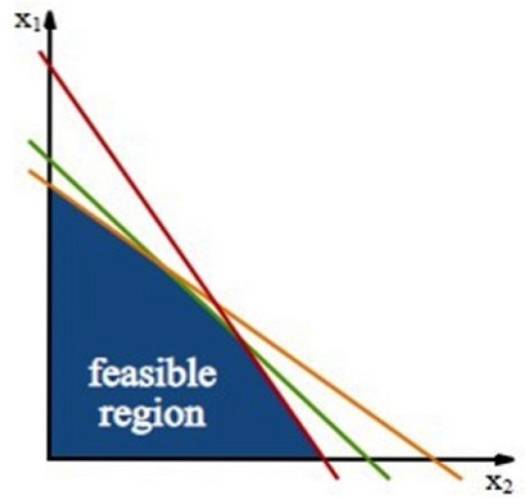
Questa regione è costruita per mezzo di linee di restrizione, quali sono le rette ottenute dalle disuguaglianze dei vincoli, lavorando solo con il segno di uguaglianza.
Nel caso del panificio che vuole ottimizzare i profitti, le linee di vincolo sono:
- x = 0
- y = 0
- 9x + 8y = 144
- 0,5 x + 0,8y = 10
Tutti i punti nella regione racchiusa da queste linee sono possibili soluzioni, quindi ce ne sono infinitamente molti. Tranne nel caso in cui la regione ammissibile risulta essere vuota, nel qual caso il problema posto non ha soluzione.
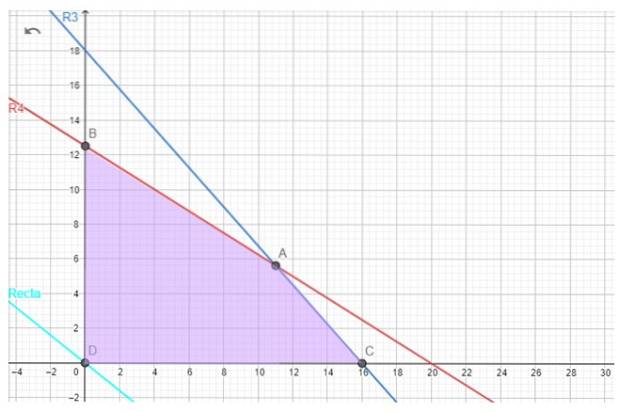
Fortunatamente per il problema della pasticceria la regione fattibile non è vuota, ce l'abbiamo di seguito.
La soluzione ottimale, se esiste, si trova con l'aiuto della funzione obiettivo. Ad esempio, quando si cerca di trovare il guadagno massimo G, abbiamo la seguente riga, che viene chiamata linea iso-profit:
G = k1x + kDuey → y = -k1x / kDue + G / kDue
Con questa retta si ottengono tutte le coppie (x, y) che forniscono un dato guadagno G, quindi esiste una famiglia di rette secondo il valore di G, ma tutte con la stessa pendenza -k1 / KDue, quindi sono linee parallele.
La soluzione ottimale
Ora, si può dimostrare che la soluzione ottima di un problema lineare è sempre un punto estremo o vertice della regione ammissibile. Poi:
La linea della soluzione è quella più lontana dall'origine e ha almeno un punto in comune con la regione ammissibile.
Se la linea più vicina all'origine ha un intero segmento in comune con la regione ammissibile, si dice che le soluzioni sono infinite. Questo caso si verifica se la pendenza della linea iso-profit è uguale a quella di una qualsiasi delle altre linee che delimitano la regione.
Per la nostra pasticceria, i vertici candidati sono A, B e C.
- Metodo simplex di Dantzig
Il metodo grafico o geometrico è applicabile a due variabili. Tuttavia, è più complicato quando ci sono tre variabili e impossibile da usare per un numero maggiore di variabili..
Quando si affrontano problemi con più di due variabili, il file metodo simplex, che consiste in una serie di algoritmi per ottimizzare le funzioni obiettivo. Le matrici e l'aritmetica semplice vengono spesso utilizzate per eseguire i calcoli.
Il metodo simplex inizia scegliendo una soluzione fattibile e verificando se è ottimale. Se lo è, abbiamo già risolto il problema, ma se non lo è, proseguiamo verso una soluzione più vicina all'ottimizzazione. Se la soluzione esiste, l'algoritmo la trova in pochi tentativi.
Applicazioni
La programmazione lineare e non lineare viene applicata in molti campi per prendere le migliori decisioni in termini di riduzione dei costi e aumento dei profitti, che non sono sempre monetari, poiché possono essere misurati nel tempo, ad esempio, se si vuole ridurre al minimo il tempo necessario eseguire una serie di operazioni.
Ecco alcuni campi:
-Nel marketing viene utilizzato per trovare la migliore combinazione di media (social network, televisione, stampa e altri) per pubblicizzare un determinato prodotto.
-Per l'assegnazione di compiti adeguati al personale di un'azienda o di uno stabilimento o programmi ad essi.
-Nella selezione degli alimenti più nutrienti e al minor costo nell'industria zootecnica e avicola.
Esercizi risolti
- Esercizio 1
Risolvi graficamente il modello di programmazione lineare sollevato nelle sezioni precedenti.
Soluzione
È necessario rappresentare graficamente l'insieme di valori determinati dal sistema di vincoli specificato nel problema:
- x ≥ 0
- e ≥0
- 9x + 8y ≤ 144
- 0,5 x + 0,8y ≤ 10
La regione data dalle disuguaglianze 1 e 2 corrisponde al primo quadrante del piano cartesiano. Per quanto riguarda le disuguaglianze 3 e 4, iniziamo trovando le linee di restrizione:
9x + 8y = 144
0,5 x + 0,8y = 10 → 5x + 8y = 100
La regione ammissibile è un quadrilatero i cui vertici sono i punti A, B, C e D.
Il profitto minimo è 0, quindi la linea 8x + 10y = 0 è il limite inferiore e le linee iso-profit hanno pendenza -8/10 = - 0,8.
Questo valore è diverso dalle pendenze delle altre linee di restrizione e poiché la regione ammissibile è delimitata, esiste la soluzione unica.
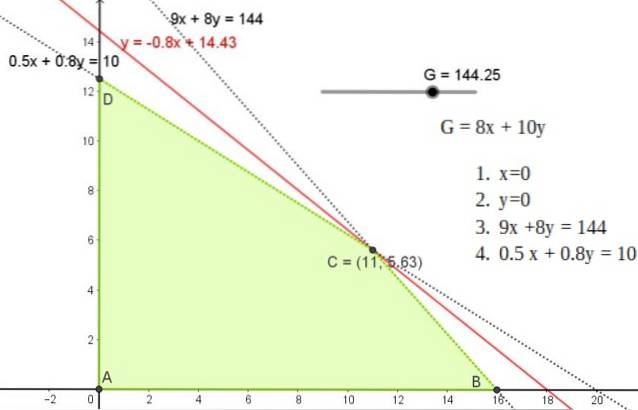
Questa soluzione corrisponde ad una retta con pendenza -0,8 che passa per uno qualsiasi dei punti A, B o C, le cui coordinate sono:
A (11; 5,625)
B (0; 12,5)
C (16, 0)
Soluzione ottimale
Calcoliamo il valore di G per ciascuno di questi punti:
-(11; 5.625): GPER = 8 x 11 + 10 x 5,625 = 144,25
-(0; 12,5): GB = 8 x 0 + 10 x 12,5 = 125
-(16, 0): G.C = 8 x 16 + 10 x 0 = 128
Il profitto più alto si trova nella produzione di 11 torte della foresta nera e 5.625 torte sacripantine. Questa soluzione corrisponde a quella trovata tramite il software.
- Esercizio 2
Verificare il risultato dell'esercizio precedente utilizzando la funzione Risolutore disponibile nella maggior parte dei fogli di calcolo come Excel o LibreOffice Calc, che incorporano l'algoritmo Simplex per l'ottimizzazione nella programmazione lineare.
Soluzione
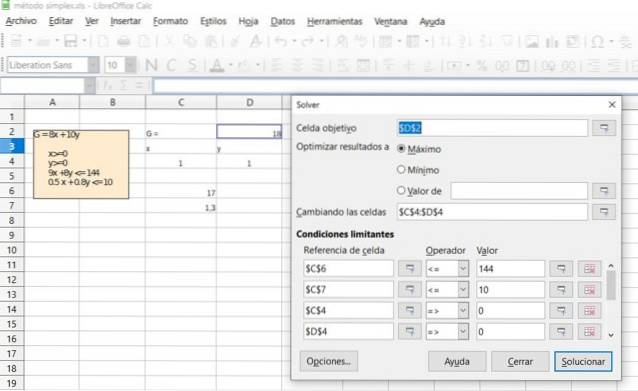
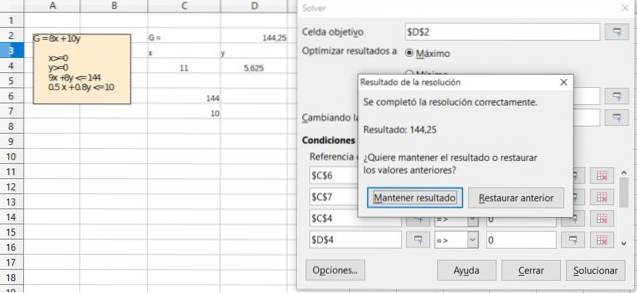
Riferimenti
- Brillante. Programmazione lineare. Estratto da: bright.org.
- Eppen, G. 2000. Ricerca operativa in scienze amministrative. 5 °. Edizione. Prentice Hall.
- Haeussler, E. 1992. Matematica per la gestione e l'economia. 2 °. Edizione. Grupo Editorial Iberoamericana.
- Hiru.eus. Programmazione lineare. Recupero da: hiru.eus.
- Wikipedia. Programmazione lineare. Estratto da: es. wikipedia.org.


Nessun utente ha ancora commentato questo articolo.