Il probabilità condizionale È la possibilità che si verifichi un determinato evento, dato che un altro si verifica come condizione. Queste informazioni aggiuntive possono (o non possono) modificare la percezione che qualcosa accadrà.
Ad esempio, possiamo chiederci: "Qual è la probabilità che piova oggi, visto che non piove da due giorni?" L'evento di cui vogliamo conoscere la probabilità è che oggi piova e l'informazione aggiuntiva che condizionerebbe la risposta è che "non piove da due giorni".
Sii un spazio probabilistico composto da Ω (spazio campionario), ℬ (gli eventi casuali) e P (la probabilità di ogni evento), più gli eventi A e B che appartengono a ℬ.
La probabilità condizionata che si verifichi A, dato che si è verificato B, che è denotata come P (A│B), è definita come segue:
P (A│B) = P (A∩B) / P (B) = P (A e B) / P (B)
Dove: P (A) è la probabilità che si verifichi A, P (B) è la probabilità dell'evento B ed è diversa da 0, e P (A∩B) è la probabilità dell'intersezione tra A e B, cioè ,, la probabilità che si verifichino entrambi gli eventi (probabilità congiunta).
Questa è un'espressione per il teorema di Bayes applicato a due eventi, proposta nel 1763 dal teologo e matematico inglese Thomas Bayes.
Indice articolo
-Ogni probabilità condizionale è compresa tra 0 e 1:
0 ≤ P (A│B) ≤ 1
-La probabilità che si verifichi l'evento A, dato che l'evento si verifica, è ovviamente 1:
P (A│A) = P (A∩A) / P (A) = P (A) / P (A) = 1
-Se due eventi sono esclusivi, cioè eventi che non possono accadere simultaneamente, la probabilità condizionale che uno di essi accada è 0, poiché l'intersezione è nulla:
P (A│B) = P (A∩B) / P (B) = 0 / P (B) = 0
-Se B è un sottoinsieme di A, anche la probabilità condizionata è 1:
P (B│A) = P (A∩B) / P (A) = 1
Importante
P (A│B) generalmente non è uguale a P (B│A), quindi bisogna stare attenti a non scambiare gli eventi quando si trova la probabilità condizionata.
Molte volte vuoi trovare la probabilità congiunta P (A∩B), piuttosto che la probabilità condizionata. Quindi, attraverso il seguente teorema abbiamo:
P (A∩B) = P (A e B) = P (A│B). P (B)
Il teorema può essere esteso per tre eventi A, B e C:
P (A∩B∩C) = P (A e B e C) = P (A) P (B│A) P (C│A∩B)
E anche per vari eventi, come A1, PERDue, PER3 e altro ancora, può essere espresso come segue:
PAPÀ1∩ ADue ∩ A3... ∩ An) = P (A1). PAPÀDue│A1). PAPÀ3│A1∩ ADue) ... PAPÀn││A1∩ ADue∩ ... An-1)
Quando si tratta di eventi che si verificano in sequenza e attraverso diverse fasi, è conveniente organizzare i dati in un diagramma o in una tabella. Ciò semplifica la visualizzazione delle opzioni per raggiungere la probabilità richiesta..
Esempi di questo sono Diagramma ad albero e il tabella di contingenza. Da uno di loro puoi costruire l'altro.
Diamo un'occhiata ad alcune situazioni in cui le probabilità di un evento vengono alterate dal verificarsi di un altro:
In un negozio di dolci vengono venduti due tipi di torte: fragola e cioccolato. Registrando le preferenze di 50 clienti di entrambi i sessi, sono stati determinati i seguenti valori:
-27 donne, di cui 11 preferiscono la torta alle fragole e 16 la torta al cioccolato.
-23 uomini: 15 scelgono il cioccolato e 8 la fragola.
La probabilità che un cliente scelga una torta al cioccolato può essere determinata applicando la regola di Laplace, secondo la quale la probabilità di qualsiasi evento è:
P = numero di eventi favorevoli / numero totale di eventi
In questo caso, su 50 clienti, un totale di 31 preferiscono il cioccolato, quindi la probabilità sarebbe P = 31/50 = 0,62. Cioè, il 62% dei clienti preferisce la torta al cioccolato.
Ma sarebbe diverso se il cliente fosse una donna? Questo è un caso di probabilità condizionata.
Utilizzando una tabella di contingenza come questa, i totali vengono visualizzati facilmente:
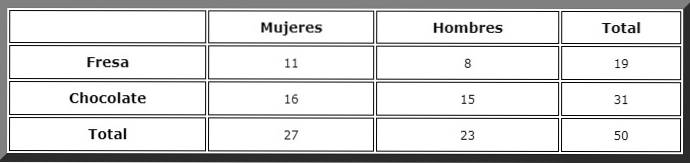
Quindi si osservano i casi favorevoli e si applica la regola di Laplace, ma prima definiamo gli eventi:
-B è l'evento "cliente femminile".
-A è l'evento "preferisco la torta al cioccolato" essendo una donna.
Andiamo alla colonna "donne" e lì vediamo che il totale è 27.
Quindi si cerca il caso favorevole nella riga "cioccolato". Ci sono 16 di questi eventi, quindi la probabilità ricercata è, direttamente:
P (A│B) = 16/27 = 0,5924
Il 59,24% delle clienti di sesso femminile preferisce la torta al cioccolato.
Questo valore coincide quando lo confrontiamo con la definizione data inizialmente di probabilità condizionata:
P (A│B) = P (A∩B) / P (B)
Ci assicuriamo di utilizzare la regola di Laplace ei valori della tabella:
P (B) = 27/50
P (A e B) = 16/50
Dove P (A e B) è la probabilità che il cliente preferisca il cioccolato ed è una donna. Ora i valori vengono sostituiti:
P (A│B) = P (A e B) / P (B) = (16/50) / (27/50) = 16/27 = 0,5924.
Ed è dimostrato che il risultato è lo stesso.
In questo esempio si applica la regola della moltiplicazione. Supponiamo che in un negozio siano esposti pantaloni di tre taglie: piccolo, medio e grande..
In un lotto con un totale di 24 pantaloni, di cui ce ne sono 8 per ogni taglia e sono tutti mischiati, quale sarebbe la probabilità di estrarne due e che entrambi fossero piccoli?
È chiaro che la probabilità di rimuovere un pantalone piccolo al primo tentativo è 8/24 = 1/3. Ora, la seconda estrazione è condizionata al primo evento, poiché quando si toglie un paio di pantaloni non ce ne sono più 24, ma 23. E se si toglie un pantalone piccolo, ci sono 7 invece di 8.
L'evento A sta tirando un piccolo pantalone, dopo averne tirato un altro al primo tentativo. E l'evento B è quello con i pantaloni piccoli per la prima volta. Perciò:
P (B) = 1/3; P (A│B) = 7/24
Infine, utilizzando la regola di moltiplicazione:
P (A∩B) = (7/24). (1/3) = 7/72 = 0,097
In uno studio sulla puntualità sui voli aerei commerciali, sono disponibili i seguenti dati:
-P (B) = 0,83, è la probabilità che un aereo decolli in tempo.
-P (A) = 0,81, è la probabilità di atterrare in tempo.
-P (B∩A) = 0.78 è la probabilità che il volo arrivi puntuale decollando puntuale.
Viene chiesto di calcolare:
a) Qual è la probabilità che l'aereo atterri in orario dato che è decollato in orario?
b) La probabilità precedente è uguale alla probabilità che sia partito in tempo se è riuscito ad atterrare in tempo??
c) E infine: qual è la probabilità che arrivi in tempo dato questo non è uscito in tempo?
Per rispondere alla domanda, viene utilizzata la definizione di probabilità condizionata:
P (A│B) = P (A∩B) / P (B) = P (A e B) / P (B) = 0,78 / 0,83 = 0,9398
In questo caso vengono scambiati gli eventi nella definizione:
P (B│A) = P (A∩B) / P (A) = P (A e B) / P (A) = 0,78 / 0,81 = 0,9630
Nota che questa probabilità è leggermente diversa dalla precedente, come abbiamo sottolineato in precedenza.
La probabilità di non partire in tempo è 1 - P (B) = 1 - 0,83 = 0,17, la chiameremo P (BC), perché è l'evento complementare per decollare in tempo. La probabilità condizionale ricercata è:
P (A│BC) = P (A∩BC) / P (BC) = P (A e BC) / P (BC)
D'altro canto:
P (A∩BC) = P (orario di atterraggio) - P (orario di atterraggio e decollo in orario) = 0,81-0,78 = 0,03
In questo caso la probabilità condizionale ricercata è:
P (A│BC) = 0,03 / 0,17 = 0,1765
Nessun utente ha ancora commentato questo articolo.