
Formula e volume del prisma quadrangolare, caratteristiche
UN Prisma quadrato È uno la cui superficie è formata da due basi uguali che sono quadrilateri e da quattro facce laterali che sono parallelogrammi. Possono essere classificati in base al loro angolo di inclinazione, nonché alla forma della loro base.
Un prisma è un corpo geometrico irregolare che ha facce piane e queste racchiudono un volume finito, che si basa su due poligoni e facce laterali che sono parallelogrammi. A seconda del numero di lati dei poligoni delle basi, i prismi possono essere: triangolari, quadrangolari, pentagonali, tra gli altri.

Caratteristiche quante facce, vertici e bordi ha?
Un prisma a base quadrangolare è una figura poliedrica che ha due basi uguali e parallele e quattro rettangoli che sono le facce laterali che uniscono i lati corrispondenti delle due basi..
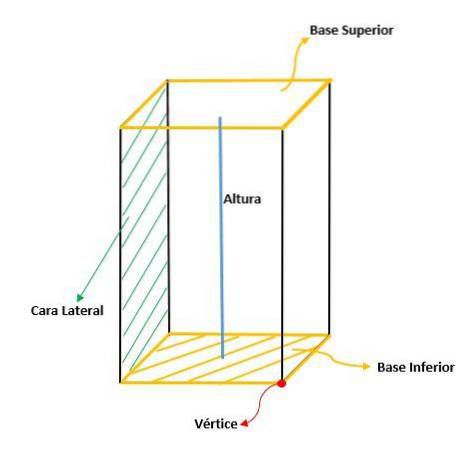
Il prisma quadrangolare può essere differenziato dagli altri tipi di prismi, perché ha i seguenti elementi:
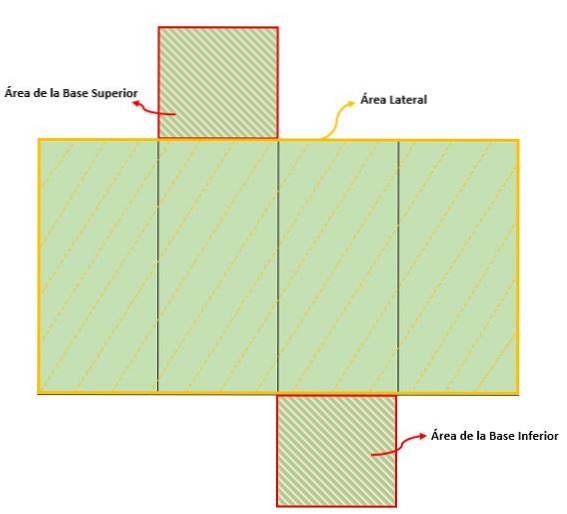
Basi (B)
Sono due poligoni formati da quattro lati (quadrilatero), uguali e paralleli.
Facce (C)
In totale, questo tipo di prisma ha sei facce:
- Quattro facce laterali formate da rettangoli.
- Due facce che sono i quadrilateri che formano le basi.
Vertici (V)
Sono quei punti in cui tre facce del prisma coincidono, in questo caso ci sono 8 vertici in totale.
Bordi: (A)
Sono segmenti in cui si incontrano due facce del prisma e questi sono:
- Bordi di base: è la linea di unione tra una faccia laterale e una base, ce ne sono 8 in totale.
- Bordi laterali: è la linea di unione laterale tra due facce, ce ne sono 4 in totale.
Il numero di spigoli di un poliedro può anche essere calcolato usando il teorema di Eulero, se si conosce il numero di vertici e facce; quindi per il prisma quadrangolare si calcola come segue:
Numero di spigoli = Numero di facce + numero di vertici - 2.
Numero di bordi = 6 + 8-2.
Numero di bordi = 12.
Altezza (h)
L'altezza del prisma quadrangolare è misurata come la distanza tra le sue due basi.
Classificazione
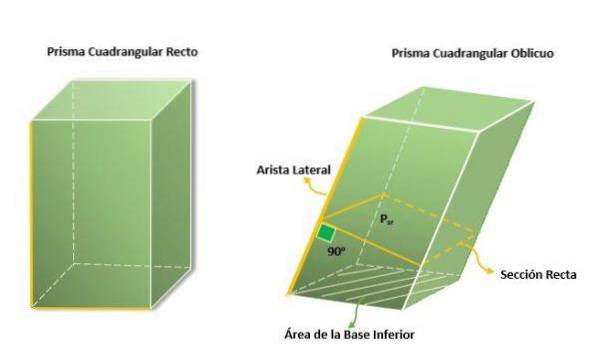
I prismi quadrangolari possono essere classificati in base al loro angolo di inclinazione, che può essere diritto o obliquo:
Prismi quadrangolari destri
Hanno due facce uguali e parallele, che sono le basi del prisma, le loro facce laterali sono formate da quadrati o rettangoli, in questo modo i loro bordi laterali saranno tutti uguali e la loro lunghezza sarà uguale all'altezza del prisma.
L'area totale è determinata dall'area e dal perimetro della sua base, dall'altezza del prisma:
A = Alato + 2Abase.
Prismi quadrangolari obliqui
Questo tipo di prisma si caratterizza perché le sue facce laterali formano angoli diedri obliqui con le basi, cioè le sue facce laterali non sono perpendicolari alla base, poiché hanno un grado di inclinazione che può essere minore o maggiore di 90o.
Le sue facce laterali sono generalmente parallelogrammi di forma romboidale o romboidale, e possono avere una o più facce rettangolari. Un'altra caratteristica di questi prismi è che la loro altezza è diversa dalla misura dei loro bordi laterali..
L'area di un prisma quadrangolare obliquo è calcolata quasi come i precedenti, sommando l'area delle basi con l'area laterale; l'unica differenza è il modo in cui viene calcolata la sua area laterale.
L'area delle laterali è calcolata con un bordo laterale e il perimetro della sezione diritta del prisma, che è proprio dove si forma un angolo di 90o con ciascuno dei lati.
PERtotale = 2 * La zonabase + PerimetroSig * Bordolato
Il volume di tutti i tipi di prismi viene calcolato moltiplicando l'area della base per l'altezza:
V = Areabase * altezza = Ab * h.
Allo stesso modo, i prismi quadrangolari possono essere classificati in base al tipo di quadrilatero che le basi formano (regolare e irregolare):
Prisma quadrangolare regolare
È uno che ha due quadrati come base e le sue facce laterali sono rettangoli uguali. Il suo asse è una linea ideale che corre parallela alle sue facce e termina al centro delle sue due basi..

Per determinare l'area totale di un prisma quadrangolare occorre calcolare l'area della sua base e l'area laterale, in modo che:
A = Alato + 2Abase.
Dove:
L'area laterale corrisponde all'area di un rettangolo; vale a dire:
PER lato = Base * Altezza = B * h.
L'area della base corrisponde all'area di un quadrato:
PER base = 2 (Side * Lato) = 2LDue
Per determinare il volume, moltiplica l'area della base per l'altezza:
V = A base * Altezza = LDue* h
Prisma quadrangolare irregolare
Questo tipo di prisma si caratterizza perché le sue basi non sono quadrate; può avere basi costituite da lati disuguali e vengono presentati cinque casi in cui:
per. Le basi sono rettangolari
La sua superficie è formata da due basi rettangolari e da quattro facce laterali anch'esse rettangolari, tutte uguali e parallele..
Per determinare la sua area totale, viene calcolata ciascuna area dei sei rettangoli che la compongono, due basi, due facce laterali piccole e le due facce laterali grandi:
Area = 2 (a* b + a*h + b*h)

b. Le basi sono diamanti:
La sua superficie è formata da due basi a forma di rombo e da quattro rettangoli che sono le facce laterali, per calcolare la sua area totale si deve determinare:
- Area di base (rombo) = (diagonale maggiore * diagonale minore) ÷ 2.
- Area laterale = perimetro della base * altezza = 4 (lati base) * h
Quindi, l'area totale è: AT = Alato + 2Abase.

c. Le basi sono romboidali
La sua superficie è formata da due basi romboidali, e da quattro rettangoli che sono le facce laterali, la sua superficie totale è data da:
- Area di base (romboidale) = base * altezza relativa = B * h.
- Area laterale = perimetro della base * altezza = 2 (lato a + lato b) * h
- Quindi l'area totale è: AT = Alato + 2Abase.
d. Le basi sono trapezi
La sua superficie è formata da due basi a forma di trapezio, e da quattro rettangoli che sono le facce laterali, la sua superficie totale è data da:
- Area di base (trapezoidale) = h * [(lato a + lato b) ÷ (2)].
- Area laterale = perimetro della base * altezza = (a + b + c + d) * h
- Quindi l'area totale è: AT = Alato + 2Abase.

e. Le basi sono trapezi
La sua superficie è formata da due basi di forma trapezoidale, e da quattro rettangoli che sono le facce laterali, la sua area totale è data da:
- Area di base (trapezio) = = (diagonale1 * diagonaleDue) ÷ 2.
- Area laterale = perimetro della base * altezza = 2 (lato a * lato b * h.
- Quindi l'area totale è: AT = Alato + 2Abase.
In sintesi, per determinare l'area di un qualsiasi prisma quadrangolare regolare, è solo necessario calcolare l'area del quadrilatero che è la base, il suo perimetro e l'altezza che avrà il prisma, in generale, la sua formula sarebbe essere:
La zona Totale = 2* La zonabase + Perimetrobase * altezza = A = 2Ab + Pb * h.
Per calcolare il volume per questi tipi di prismi, viene utilizzata la stessa formula che è:
Volume = Areabase * altezza = Ab * h.
Riferimenti
- Ángel Ruiz, H. B. (2006). Geometrie. Tecnologia CR, .
- Daniel C. Alexander, G. M. (2014). Geometria elementare per studenti universitari. Cengage Learning.
- Maguiña, R. M. (2011). Sfondo di geometria. Lima: Centro pre-universitario UNMSM.
- Ortiz Francisco, O. F. (2017). Matematica 2.
- Pérez, A. Á. (1998). Álvarez Second Grade Encyclopedia.
- Pugh, A. (1976). Poliedri: un approccio visivo. California: Berkeley.
- Rodríguez, F. J. (2012). Geometria descrittiva Volume I. Sistema diedro. Donostiarra Sa.



Nessun utente ha ancora commentato questo articolo.