Il potenza meccanica è la velocità con cui viene svolto il lavoro, espressa matematicamente dalla quantità di lavoro svolto per unità di tempo. E poiché il lavoro viene svolto a scapito dell'energia assorbita, può anche essere dichiarato come energia per unità di tempo.
Chiamando P per dare potenza, W lavorare, E all'energia e t Allo stesso tempo, tutto quanto sopra può essere riassunto in espressioni matematiche di facile utilizzo:
O bene:
Altre unità di potenza utilizzate nelle industrie sono hp (potenza di cavallo o potenza) e CV (potenza). L'origine di queste unità risale anche a James Watt e alla rivoluzione industriale, quando lo standard di misurazione era la velocità con cui un cavallo lavorava..
Sia hp che CV sono approssimativamente equivalenti a ¾ kilo-W e sono ancora ampiamente utilizzati, soprattutto nell'ingegneria meccanica, ad esempio nella designazione dei motori.
I multipli del watt, come il già citato kilo-W = 1000 W, sono spesso usati anche nell'energia elettrica. Questo perché il joule è un'unità di energia relativamente piccola. Il sistema britannico utilizza libbra-piedi / secondo.
Indice articolo
Il concetto di potenza è applicabile a tutti i tipi di energia, sia meccanica, elettrica, chimica, eolica, sonora o di qualsiasi tipo. Il tempo è molto importante nel settore, perché i processi devono essere eseguiti il più rapidamente possibile.
Qualsiasi motore farà il lavoro necessario purché abbia abbastanza tempo, ma l'importante è farlo nel più breve tempo possibile, per aumentare l'efficienza..
Viene subito descritta un'applicazione molto semplice per chiarire bene la distinzione tra lavoro e potenza.
Supponiamo che un oggetto pesante venga tirato da una fune. Per fare ciò, è necessario un agente esterno per eseguire il lavoro necessario. Supponiamo che questo agente trasferisca 90 J di energia al sistema di stringhe di oggetti, in modo che si metta in moto per 10 secondi.
In tal caso, la velocità di trasferimento dell'energia è di 90 J / 10 so 9 J / s. Quindi possiamo affermare che quell'agente, una persona o un motore, ha una potenza di uscita di 9 W..
Se un altro agente esterno è in grado di ottenere lo stesso spostamento, in meno tempo o trasferendo meno energia, allora è in grado di sviluppare una maggiore potenza..
Un altro esempio: supponiamo un trasferimento di energia di 90 J, che riesca a mettere in moto il sistema per 4 secondi. La potenza in uscita sarà di 22,5 W..
La potenza è strettamente correlata alle prestazioni. L'energia fornita a una macchina non si trasforma mai completamente in lavoro utile. Una parte importante viene solitamente dissipata in calore, che dipende da molti fattori, ad esempio il design della macchina.
Ecco perché è importante conoscere le prestazioni delle macchine, che si definisce come il quoziente tra il lavoro erogato e l'energia erogata:
η = lavoro fornito dalla macchina / energia fornita
Dove la lettera greca η denota la resa, una quantità adimensionale che è sempre minore di 1. Se viene anche moltiplicata per 100, abbiamo la resa in termini percentuali.
- Gli esseri umani e gli animali sviluppano potenza durante la locomozione. Ad esempio, salire le scale richiede un lavoro contro la gravità. Confrontando due persone che salgono una scala, quella che sale per prima tutti i gradini avrà sviluppato più potenza dell'altra, ma entrambi hanno fatto lo stesso lavoro.
- Gli elettrodomestici e le macchine hanno la loro potenza di uscita specificata. Una lampadina a incandescenza adatta per illuminare bene una stanza ha una potenza di 100 W. Ciò significa che la lampadina trasforma l'energia elettrica in luce e calore (la maggior parte) ad una velocità di 100 J / s.
- Il motore di un tosaerba può consumare circa 250 W e quello di un'auto è nell'ordine dei 70 kW.
- Una pompa dell'acqua fatta in casa di solito fornisce 0,5 hp.
- Il sole genera 3,6 x 10 26 Potenza W.
La potenza istantanea si ottiene impiegando un tempo infinitesimale: P = dW / dt. La forza che produce il lavoro provocando il piccolo spostamento infinitesimale dX è F (entrambi sono vettori), quindi dW = F ● dX. Sostituendo tutto nell'espressione per il potere, rimane:
Le persone sono in grado di generare una potenza di circa 1500 W o 2 cavalli, almeno per un breve periodo, come il sollevamento di pesi.
In media, la potenza giornaliera (8 ore) è di 0,1 CV a persona. Gran parte del quale si traduce in calore, più o meno la stessa quantità generata da una lampadina a incandescenza da 75W.
Un atleta in allenamento può generare in media 0,5 hp equivalenti a circa 350 J / s, trasformando l'energia chimica (glucosio e grasso) in energia meccanica.
Quando si parla di potenza umana, è generalmente preferibile misurare in chilocalorie / ora, piuttosto che in watt. L'equivalenza necessaria è:
1 chilocaloria = 1 caloria nutrizionale = 4186 J.
Una potenza di 0,5 hp suona come una quantità molto piccola ed è per molte applicazioni.
Tuttavia, nel 1979 è stata creata una bicicletta a propulsione umana in grado di volare. Paul MacCready ha progettato il Gossamer Albatross, che ha attraversato la Manica generando 190 W di potenza media (figura 1).
Un'importante applicazione è la distribuzione dell'energia elettrica tra gli utenti. Le aziende che forniscono la bolletta dell'elettricità per l'energia consumata, non per la tariffa con cui viene consumata. Ecco perché chi legge attentamente la bolletta troverà un'unità molto specifica: il chilowattora o kW-h..
Tuttavia, quando il nome Watt è incluso in questa unità, si riferisce all'energia e non alla potenza..
Il chilowattora viene utilizzato per indicare il consumo di energia elettrica, poiché il joule, come detto prima, è un'unità abbastanza piccola: 1 wattora o W-h è il lavoro svolto in 1 ora utilizzando una potenza di 1 watt.
Perciò 1 kW-h è il lavoro che si fa in un'ora lavorando con una potenza di 1kW o 1000 W. Mettiamo i numeri per convertire queste quantità in joule:
1 L-A = 1 L x 3600 S = 3600 J
1 kW-h = 1000 W x 3600 s = 3,6 x 10 6 J
Si stima che una famiglia possa consumare circa 200 kW-ora al mese.
Un agricoltore utilizza un trattore per tirare una balla di fieno di M = 150 kg su un piano inclinato di 15 ° e trasportarla alla stalla, alla velocità costante di 5,0 km / h. Il coefficiente di attrito cinetico tra la balla di fieno e lo scivolo è 0,45. Trovare la potenza del trattore.
Per questo problema è necessario disegnare un diagramma a corpo libero per la balla di fieno che sale in pendenza. Essere F la forza applicata dal trattore per sollevare la balla, α = 15º è l'angolo di inclinazione.
Inoltre, è coinvolta la forza di attrito cinetico Ftoccare che si oppone al movimento, più il normale N e il peso W (non confondere la W del peso con quella del lavoro).
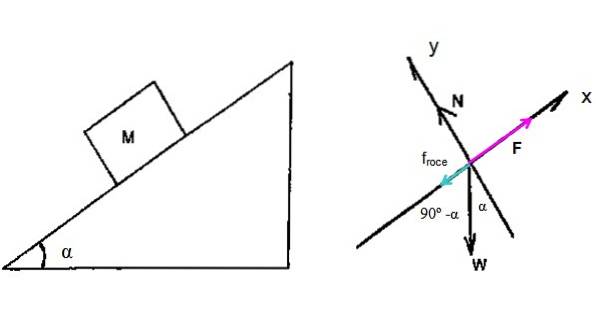
La seconda legge di Newton offre le seguenti equazioni:
∑ Fx = F -WX -Ftoccare = 0 (poiché la balla sale a velocità costante)
∑Fy = N - WY = 0 (non c'è movimento lungo l'asse x)
La forza di attrito cinetico è calcolata da:
Ftoccare = coefficiente di attrito cinetico x grandezza del normale
Ftoccare = 0,45. Wy = 0,45 x 150 kg x9,8 m / s2 x cos 15º = 639 N
F = WX + Ftoccare = M.g. sin α = 150 kg. 9,8 m / sDue . peccato 15º + 639 N = 1019.42 N
Velocità e forza hanno la stessa direzione e senso, quindi:
P = F ● v = F. v
È necessario trasformare le unità della velocità:
v = 5,0 km / h = 1,39 m / s
Sostituendo i valori, finalmente otteniamo:
P = 1019,42 N x 1,39 m / s = 1417 W = 1,4 kW
Il motore mostrato in figura solleverà il blocco da 2 kg, partendo da fermo, con un'accelerazione di 2 m / sDue e in 2 secondi.
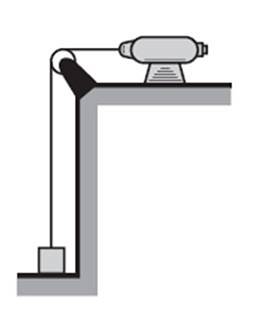
Calcolare:
a) L'altezza raggiunta dal blocco in quel tempo.
b) La potenza che il motore deve sviluppare per raggiungere questo obiettivo.
a) È un moto rettilineo uniformemente variato, pertanto verranno utilizzate le equazioni corrispondenti, con velocità iniziale 0. L'altezza raggiunta è data da:
y = ½ aDue = ½. 2 m / sDue . (2 s)Due = 4 m.
b) Per trovare la potenza sviluppata dal motore si può utilizzare l'equazione:
P = ΔW / Δt
E poiché la forza esercitata sul blocco è attraverso la tensione della corda, che è di grandezza costante:
P = (ma) .y / Δt = 2 kg x 2 m / sDue x 4 m / 2 s = 8 W.
Nessun utente ha ancora commentato questo articolo.