
Proprietà, elementi, angoli, esempi di poligoni regolari
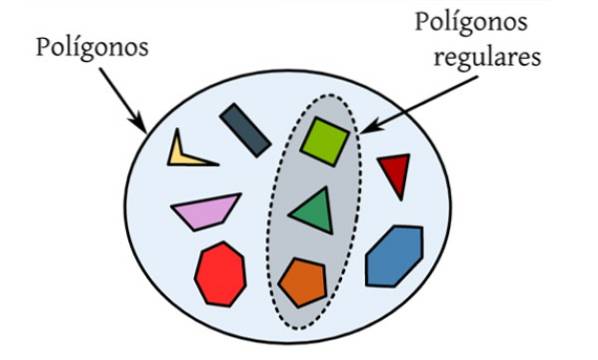
Il poligoni regolari sono quelli che hanno tutti i lati e gli angoli interni uguali. Nella figura seguente è presente un insieme di diversi poligoni, che sono figure piane limitate da una curva chiusa e solo quelle evidenziate soddisfano le condizioni per essere regolari.
Ad esempio, il triangolo equilatero è un poligono regolare, poiché i suoi tre lati misurano lo stesso, così come i suoi angoli interni, che valgono 60º ciascuno..
Il quadrato è un quadrilatero con quattro lati di uguale misura e i cui angoli interni sono di 90º. È seguito dal pentagono regolare, con cinque lati di uguale dimensione e cinque angoli interni di 108º ciascuno..
Quando un poligono è regolare, questa parola viene aggiunta al suo nome speciale, quindi abbiamo l'esagono regolare, l'ettagono regolare e così via.
Indice articolo
- 1 Proprietà dei poligoni regolari
- 2 Elementi di un poligono regolare
- 2.1 Vertice
- 2.2 Lato
- 2.3 Diagonale
- 2.4 Centro
- 2.5 Radio
- 2.6 Apothem
- 2.7 Angolo centrale
- 2.8 Sagita
- 3 Perimetro e area
- 3.1 Perimetro
- 3.2 Area
- 4 angoli
- 4.1 Angolo centrale
- 4.2 Angolo interno o angolo interno
- 4.3 Angoli esterni
- 5 Esempi di poligoni regolari
- 5.1 - Poligoni regolari nella vita quotidiana e nella natura
- 5.2 - Esagoni regolari in natura
- 6 Esercizio risolto
- 6.1 Soluzione
- 7 Riferimenti
Proprietà dei poligoni regolari
Le proprietà più importanti dei poligoni regolari possono essere riassunte come segue:
-I lati misurano lo stesso, quindi lo sono equilatero.
-Sono equiangolare, poiché tutti i suoi angoli interni hanno la stessa misura.
-Possono sempre essere inscritti in una circonferenza, il che significa che si adattano perfettamente a uno, che viene chiamato circonferenza circoscritta.
-Per un poligono regolare con n lati, la misura di un angolo interno α è:
α = [180 (n-2)] / n
-Puoi disegnare n (n-3) / 2 diagonali dai vertici di un poligono, che sia regolare o meno.
-La somma dei angoli esterni è uguale a 360º.

Elementi di un poligono regolare
Successivamente presentiamo gli elementi principali di un poligono regolare, visualizzati nella figura sottostante.

Vertice
Punto comune che hanno due lati consecutivi, indicato come V nella figura.
Lato
È il segmento che unisce due vertici consecutivi del poligono ed è indicato come ℓ o L.
Diagonale
Segmento che unisce due vertici non consecutivi del poligono, nella figura è indicato come d.
Centro
È il centro comune del cerchio inscritto e del cerchio circoscritto, indicato dalla lettera O. Può anche essere visto come l'unico punto equidistante sia dai vertici che dai punti medi di ciascun lato..
Radio
È la radio r del cerchio circoscritto e coincide con la distanza tra O e un vertice.
Apotema
È chiamato apotema al raggio della circonferenza inscritto nel poligono, rappresentato in figura con una lettera per. L'apotema è perpendicolare a un lato e lo congiunge con il centro O (segmento rosso in figura 3).
Conoscendo il raggio re la lunghezza del lato, l'apotema si calcola da:
Poiché, in effetti, l'apotema è una delle gambe di un triangolo rettangolo (vedi figura 3), l'altra gamba è il valore di ℓ / 2 (metà di un lato) e l'ipotenusa il raggio r del poligono.
Applicando il teorema di Pitagora a detto triangolo si ottiene questa equazione, che vale non solo per l'esagono, ma per ogni poligono regolare.
Angolo centrale
È l'angolo il cui vertice coincide con il centro O ei cui lati sono i segmenti che uniscono il centro con due vertici consecutivi. La sua misura in gradi sessagesimali è 360º / n, dove n è il numero di lati del poligono.
Sagita
È la differenza tra il raggio del poligono e l'apotema (vedi figura 3). Denotando la sagitta come S:
S = r - a
Perimetro e area
Perimetro
Si calcola facilmente sommando le lunghezze dei lati. Poiché ogni lato ha lunghezza L uguale e ci sono n lati, il perimetro P è espresso come:
P = n.L
La zona
In un poligono regolare l'area A è data dal prodotto tra il semiperimetro (metà del perimetro) e la lunghezza dell'apotema per.
A = P.a / 2
Poiché il perimetro dipende dal numero di lati n, risulta che:
A = (nL) .a / 2
Due poligoni regolari possono avere lo stesso perimetro anche se non hanno lo stesso numero di lati, poiché dipenderebbe poi dalla lunghezza dei lati.
Nel suo libro V Collezione, il matematico Pappo d'Alessandria (290-350), l'ultimo dei grandi matematici della Grecia antica, dimostrò che tra tutti i poligoni regolari con lo stesso perimetro, quello con l'area maggiore è quello con il maggior numero di lati.
Angoli
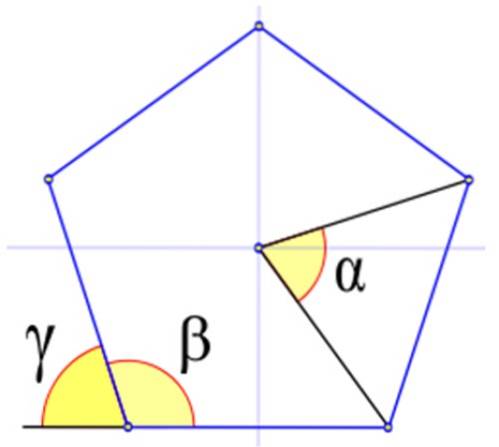
La figura 4 mostra gli angoli rilevanti in un poligono regolare, indicati con le lettere greche α, β e γ.
Angolo centrale
In precedenza abbiamo accennato all'angolo centrale, tra gli elementi del poligono regolare, è l'angolo il cui vertice è al centro del poligono ei lati sono i segmenti che uniscono il centro con due vertici consecutivi.
Per calcolare la misura dell'angolo centrale α, dividere 360º per n, il numero di lati. Oppure 2π radianti tra n:
α = 360º / n
Equivalente in radianti a:
α = 2π / n
Angolo interno o angolo interno
Nella figura 4 l'angolo interno β è quello il cui vertice coincide con uno della figura e anche i suoi lati sono lati della figura. Viene calcolato in gradi sessagesimali da:
β = [180 (n-2)] / n
O in radianti usando:
β = [π (n-2)] / n
Angoli esterni
Sono indicati con la lettera greca γ. La figura mostra che γ + β = 180º. Perciò:
γ = 180º - β
La somma di tutti gli angoli esterni a un poligono regolare è di 360º.

Esempi di poligoni regolari
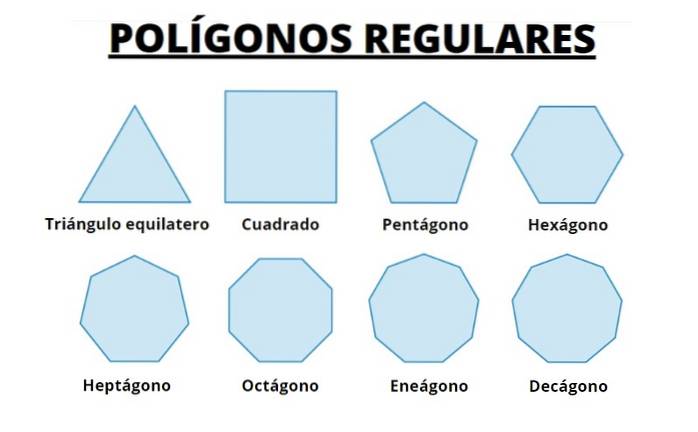
Successivamente abbiamo i primi 8 poligoni regolari. Osserviamo che all'aumentare del numero di lati, il poligono assomiglia sempre di più alla circonferenza in cui sono inscritti.
Possiamo immaginare che riducendo la lunghezza dei lati e aumentando il numero di questi, otteniamo la circonferenza.
- Poligoni regolari nella vita quotidiana e nella natura
I poligoni regolari si trovano ovunque nella vita di tutti i giorni e anche in natura. Diamo un'occhiata ad alcuni esempi:
Segnali stradali
Poligoni regolari come triangoli equilateri, quadrati e rombi abbondano nella segnaletica che vediamo su autostrade e strade. Nella figura 6 vediamo un segnale di stop di forma ottagonale.

Mobilia
Innumerevoli mobili hanno il quadrato, ad esempio, come la loro caratteristica figura geometrica, così come molti tavoli, sedie e panche sono quadrati. Un parallelepipedo è generalmente una scatola con lati a forma di rettangolo (che non è un poligono regolare), ma possono anche essere quadrati..
Architettura e costruzione
Le piastrelle su pavimenti e pareti, sia nelle case che nelle strade, hanno spesso la forma di poligoni regolari..
Le tassellature sono superfici ricoperte interamente da piastrelle che hanno diverse forme geometriche. Con il triangolo, il quadrato e l'esagono si possono realizzare tassellature regolari, quelle che utilizzano un solo tipo di figura per ricoprire perfettamente, senza lasciare spazi vuoti (vedi figura 6).
Allo stesso modo, gli edifici fanno uso di poligoni regolari in elementi come finestre e decorazioni..

- Esagoni regolari in natura
Sorprendentemente, l'esagono regolare è un poligono che appare frequentemente in natura..
I favi realizzati dalle api per conservare il miele hanno la forma molto vicina ad un esagono regolare. Come osservava Pappo d'Alessandria, in questo modo le api ottimizzano lo spazio per immagazzinare quanto più miele possibile..
E ci sono anche esagoni regolari nel guscio delle tartarughe e nei fiocchi di neve, che adottano anche varie forme geometriche molto belle..
Esercizio risolto
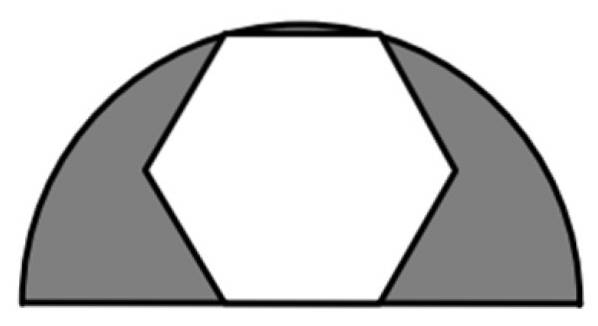
Un esagono regolare è inscritto in un semicerchio di raggio 6 cm, come mostrato in figura. Qual è il valore dell'area ombreggiata?
Soluzione
L'area ombreggiata è la differenza tra l'area del semicerchio con raggio R = 6 cm e l'area dell'intero esagono, un poligono regolare a 6 lati. Quindi avremo bisogno di formule per l'area di ciascuna di queste figure.
Area semicerchio
PER1 = π RDue / 2 = π (6 cm)Due / 2 = 18π cmDue
Area esagonale regolare
La formula per calcolare l'area di un poligono regolare è:
A = P.a / 2
Dove P è il perimetro e per è l'apotema. Poiché il perimetro è la somma dei lati, avremo bisogno del valore di questi. Per l'esagono regolare:
P = 6ℓ
Perciò:
A = 6ℓa / 2
Per trovare il valore del lato ℓ è necessario costruire figure ausiliarie, che spiegheremo di seguito:
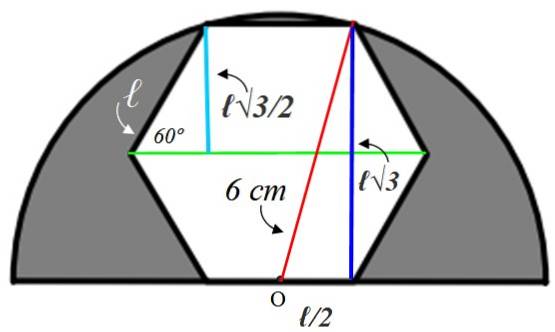
Cominciamo con il piccolo triangolo rettangolo a sinistra, la cui ipotenusa è ℓ. Un angolo interno dell'esagono è uguale a:
α = [180 (n-2)] / n = α = [180 (6-2)] / 6 = 120º
Il raggio che abbiamo tracciato in verde divide in due questo angolo, quindi l'angolo acuto del triangolo piccolo è di 60º. Con le informazioni fornite, questo triangolo viene risolto, trovando il lato azzurro, che misura la stessa dell'apotema:
Gamba opposta = a = ℓ x sin 60º = ℓ√3 / 2 cm
Questo valore è il doppio della gamba blu scuro del triangolo grande a destra, ma da questo triangolo sappiamo che l'ipotenusa misura 6 cm perché è il raggio del semicerchio. La gamba rimanente (in basso) è uguale a ℓ / 2 poiché il punto O è al centro del lato.
Poiché gli angoli interni di questo triangolo non sono noti, possiamo affermare il teorema di Pitagora per esso:
36 = 3 ℓDue + ℓDue / 4
(13/4) ℓDue = 36 → ℓ = √ (4 x36) / 13 cm = 12 / √13 cm
Con questo valore si calcola l'apotema:
a = ℓ√3 / 2 cm = (12 / √13) x (√3 / 2) cm = 6√3 / √13 cm
ChiamiamoDue all'area dell'esagono regolare:

= 28,8 cmDue
Area della figura ombreggiata
PER1 - PERDue = 18π cmDue - 28,8 cmDue = 27,7 cmDue
Riferimenti
- Baldor, A. 1973. Geometria e trigonometria. Casa editrice culturale centroamericana.
- Goditi la matematica. Mosaici. Estratto da: gustolasmatematicas.com.
- E. A. 2003. Elementi di geometria: con esercizi e geometria della bussola. Università di Medellin.
- Esagoni in natura. Estratto da: malvargamath.wordpress.com.
- Jiménez, R. 2010. Matematica II. Geometria e trigonometria. Seconda edizione. Prentice Hall.
- Poligoni regolari. Estratto da: mate.ingenieria.usac.edu.gt.
- Wikipedia. Apotema. Estratto da: es.wikipedia.org.



Nessun utente ha ancora commentato questo articolo.