
Caratteristiche, proprietà, formule, tipi delle onde meccaniche
UN onda meccanica è un disturbo che necessita di un mezzo fisico per diffondersi. L'esempio più vicino è nel suono, in grado di essere trasmesso attraverso un gas, un liquido o un solido.
Altre onde meccaniche ben note sono quelle prodotte quando viene pizzicata la corda tesa di uno strumento musicale. O le tipiche increspature circolari provocate da un sasso lanciato in uno stagno.

Il disturbo viaggia attraverso il mezzo producendo vari spostamenti nelle particelle che lo compongono, a seconda del tipo di onda. Mentre l'onda passa, ogni particella nel mezzo compie movimenti ripetitivi che la separano brevemente dalla sua posizione di equilibrio..
La durata del disturbo dipende dalla sua energia. Nel moto ondoso, l'energia è ciò che si propaga da un lato all'altro del mezzo, poiché le particelle vibranti non si allontanano mai troppo dal loro luogo di origine.
L'onda e l'energia che trasporta possono percorrere grandi distanze. Quando l'onda scompare, è perché la sua energia ha finito per dissiparsi nel mezzo, lasciando tutto calmo e silenzioso come prima del disturbo.
Indice articolo
- 1 Tipi di onde meccaniche
- 1.1 Onde trasversali
- 1.2 Onde longitudinali
- 1.3 Onde di superficie
- 1.4 Esempi dei diversi tipi di onde: movimenti sismici
- 2 Caratteristiche e proprietà
- 2.1 Ampiezza e lunghezza d'onda delle onde
- 2.2 Periodo e frequenza
- 2.3 Frequenza angolare
- 3 Formule ed equazioni
- 4 esempi lavorati
- 4.1 Esercizio 1
- 4.2 Soluzione
- 4.3 Esercizio 2
- 4.4 Soluzione
- 5 Suono: un'onda longitudinale
- 6 Le caratteristiche del suono: frequenza e intensità
- 6.1 Frequenza
- 6.2 Intensità
- 7 esperimenti pratici per bambini
- 7.1 -Esperimento 1: Intercom
- 7.2 -Esperimento 2: Osservare le onde
- 8 Riferimenti
Tipi di onde meccaniche
Le onde meccaniche sono classificate in tre gruppi principali:
- Onde trasversali.
- Onde longitudinali.
- Onde di superficie.
Onde trasversali
Nelle onde di taglio, le particelle si muovono perpendicolarmente alla direzione di propagazione. Ad esempio, le particelle della stringa nella figura seguente oscillano verticalmente mentre l'onda si sposta da sinistra a destra:

Onde longitudinali
Nelle onde longitudinali la direzione di propagazione e la direzione di movimento delle particelle sono parallele.
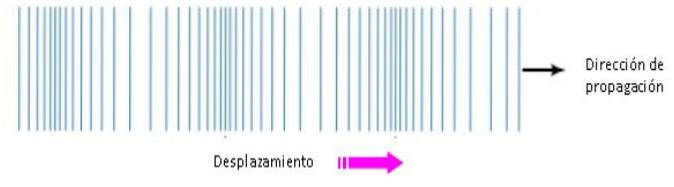
Onde di superficie
In un'onda marina, le onde longitudinali e le onde trasversali sono combinate sulla superficie, quindi sono onde di superficie, che viaggiano sul confine tra due diversi mezzi: acqua e aria, come mostrato nella figura seguente.
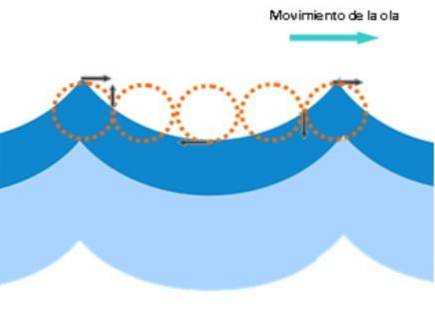
Quando si infrangono le onde sulla riva, predominano i componenti longitudinali. Per questo motivo, si osserva che le alghe vicino alla riva hanno un movimento avanti e indietro..
Esempi dei diversi tipi di onde: movimenti sismici
Durante i terremoti, vengono prodotti vari tipi di onde che viaggiano sul globo, comprese le onde longitudinali e le onde trasversali..
Le onde sismiche longitudinali sono chiamate onde P, mentre quelle trasversali sono onde S..
Il nome P è dovuto al fatto che sono onde di pressione e sono anche primarie quando arrivano per prime, mentre quelle trasversali sono S per "taglio" o taglio e sono anche secondarie, poiché arrivano dopo la P.
Caratteristiche e proprietà
Le onde gialle nella Figura 2 sono onde periodiche, costituite da disturbi identici che si muovono da sinistra a destra. Nota che entrambi per Che cosa b hanno lo stesso valore in ciascuna delle regioni d'onda.
Le perturbazioni dell'onda periodica si ripetono sia nel tempo che nello spazio, assumendo la forma di una curva sinusoidale caratterizzata dall'avere picchi o picchi, che sono i punti più alti, e valli dove si trovano i punti più bassi..
Questo esempio servirà per studiare le caratteristiche più importanti delle onde meccaniche.
Ampiezza e lunghezza d'onda delle onde
Supponendo che l'onda nella Figura 2 rappresenti una corda vibrante, la linea nera funge da riferimento e divide il treno d'onde in due parti simmetriche. Questa linea coinciderebbe con la posizione in cui la fune è a riposo.
Il valore di a è chiamato l'ampiezza dell'onda ed è solitamente indicato dalla lettera A. Da parte sua, la distanza tra due valli o due creste successive è la lunghezza d'onda le corrisponde alla grandezza chiamata b in figura 2.
Periodo e frequenza
Essendo un fenomeno ripetitivo nel tempo, l'onda ha un periodo T che è il tempo necessario per compiere un ciclo completo, mentre la frequenza f è l'inverso o reciproco del periodo e corrisponde al numero di cicli effettuati per unità di tempo.
La frequenza f ha come unità nel Sistema Internazionale l'inverso del tempo: s-1 o Hertz, in onore di Heinrich Hertz, che scoprì le onde radio nel 1886. 1 Hz è interpretato come la frequenza equivalente a un ciclo o vibrazione al secondo.
Velocità v La forma d'onda mette in relazione la frequenza con la lunghezza d'onda:
v = λ.f = l / T
Frequenza angolare
Un altro concetto utile è la frequenza angolare ω data da:
ω = 2πf
La velocità delle onde meccaniche è diversa a seconda del mezzo in cui viaggiano. Come regola generale, le onde meccaniche hanno una velocità maggiore quando viaggiano attraverso un solido e sono più lente nei gas, compresa l'atmosfera..
In generale, la velocità di molti tipi di onde meccaniche viene calcolata dalla seguente espressione:

Ad esempio, per un'onda che viaggia lungo una corda, la velocità è data da:
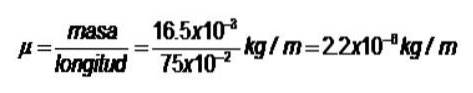
La tensione nella corda tende a riportare la corda nella sua posizione di equilibrio, mentre la densità di massa impedisce che ciò avvenga immediatamente..
Formule ed equazioni
Le seguenti equazioni sono utili per risolvere gli esercizi che seguono:
Frequenza angolare:
ω = 2πf
Periodo:
T = 1 / f
Densità di massa lineare:
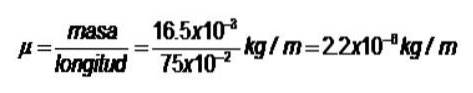
v = λ.f
v = λ / T
v = λ / 2π
Velocità dell'onda che si propaga in una stringa:
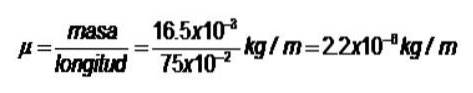
Esempi lavorati
Esercizio 1
L'onda sinusoidale mostrata nella Figura 2 viaggia nella direzione dell'asse positivo delle x e ha una frequenza di 18,0 Hz. È noto che 2a = 8,26 cm eb / 2 = 5,20 cm. Trova:
a) Ampiezza.
b) Lunghezza d'onda.
c) Periodo.
d) Velocità delle onde.
Soluzione
a) L'ampiezza è a = 8,26 cm / 2 = 4,13 cm
b) La lunghezza d'onda è l = b = 2 x20 cm = 10,4 cm.
c) Il periodo T è l'inverso della frequenza, quindi T = 1 / 18,0 Hz = 0,056 s.
d) La velocità dell'onda è v = l.f = 10,4 cm. 18 Hz = 187,2 cm / s.
Esercizio 2
Un filo sottile lungo 75 cm ha una massa di 16,5 g. Una delle sue estremità è fissata a un chiodo, mentre l'altra ha una vite che permette di regolare la tensione nel filo. Calcolare:
a) La velocità di questa onda.
b) La tensione in newton necessaria affinché un'onda trasversale la cui lunghezza d'onda è di 3,33 cm vibri a una velocità di 625 cicli al secondo.
Soluzione
a) Usando v = λ.f, valido per qualsiasi onda meccanica e sostituendo valori numerici, si ottiene:
v = 3,33 cm x 625 cicli / secondo = 2081,3 cm / s = 20,8 m / s
b) La velocità dell'onda che si propaga attraverso una stringa è:
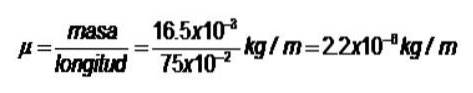
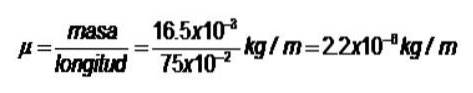
La tensione T nella corda si ottiene alzandola al quadrato su entrambi i lati dell'uguaglianza e risolvendo:
T = vDue.μ = 20,8Due . 2,2 x 10-6 N = 9,52 x 10-4 N.
Suono: un'onda longitudinale
Il suono è un'onda longitudinale, molto facile da visualizzare. Per questo hai solo bisogno di un file slinky, una molla elicoidale flessibile con cui è possibile eseguire molti esperimenti per determinare la forma delle onde.
Un'onda longitudinale è costituita da un impulso che comprime ed espande alternativamente il mezzo. L'area compressa è chiamata "compressione" e l'area in cui le spire della molla sono più lontane è "espansione" o "rarefazione". Entrambe le zone si muovono lungo l'asse assiale dello slinky e formano un'onda longitudinale.
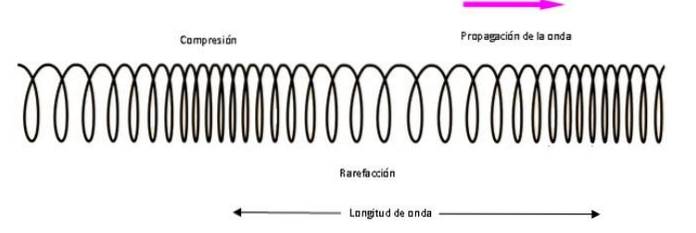
Allo stesso modo in cui una parte della molla viene compressa e l'altra si allunga mentre l'energia si muove insieme all'onda, il suono comprime porzioni d'aria che circondano la fonte del disturbo. Per questo motivo non può propagarsi nel vuoto.
Per le onde longitudinali, i parametri sopra descritti sono ugualmente validi per le onde periodiche trasversali: ampiezza, lunghezza d'onda, periodo, frequenza e velocità dell'onda..
La figura 5 mostra la lunghezza d'onda di un'onda longitudinale che viaggia lungo una molla elicoidale..
In esso sono stati selezionati due punti situati al centro di due compressioni successive per indicare il valore della lunghezza d'onda.
Le compressioni sono l'equivalente delle creste e le espansioni sono l'equivalente delle valli in un'onda trasversale, quindi un'onda sonora può essere rappresentata anche da un'onda sinusoidale.
Le caratteristiche del suono: frequenza e intensità
Il suono è un tipo di onda meccanica con diverse proprietà molto speciali, che lo distinguono dagli esempi che abbiamo visto finora. Successivamente vedremo quali sono le sue proprietà più rilevanti.
Frequenza
La frequenza del suono è percepita dall'orecchio umano come un suono acuto (alte frequenze) o basso (basse frequenze).
La gamma di frequenze udibili nell'orecchio umano è compresa tra 20 e 20.000 Hz. Sopra i 20.000 Hz ci sono i suoni chiamati ultrasuoni e sotto gli infrasuoni, frequenze non udibili dall'uomo, ma che i cani e altri animali possono percepire e utilizzare.
Ad esempio, i pipistrelli emettono onde ultrasoniche con il naso per determinare la loro posizione al buio e anche per la comunicazione..
Questi animali hanno sensori con i quali ricevono le onde riflesse e in qualche modo interpretano il tempo di ritardo tra l'onda emessa e l'onda riflessa e le differenze nella loro frequenza e intensità. Con questi dati deducono la distanza che hanno percorso, e in questo modo sono in grado di sapere dove si trovano gli insetti e di volare tra gli anfratti delle grotte in cui vivono..
I mammiferi marini come la balena e il delfino hanno un sistema simile: hanno organi specializzati pieni di grasso nella testa, con i quali emettono suoni, e i corrispondenti sensori nelle loro mascelle che rilevano il suono riflesso. Questo sistema è noto come ecolocalizzazione.
Intensità
L'intensità dell'onda sonora è definita come l'energia trasportata per unità di tempo e per unità di area. L'energia per unità di tempo è potenza. Pertanto l'intensità del suono è la potenza per unità di superficie ed è espressa in watt / mDue o W / mDue. L'orecchio umano percepisce l'intensità dell'onda come volume: più forte è la musica, più forte sarà.
L'orecchio rileva intensità comprese tra 10-12 e 1 W / mDue senza provare dolore, ma il rapporto tra intensità e volume percepito non è lineare. Per produrre un suono con il doppio del volume, è necessaria un'onda con un'intensità 10 volte maggiore.
Il livello di intensità sonora è un'intensità relativa che viene misurata su una scala logaritmica, in cui l'unità è il bel e più frequentemente il decibel o decibel..
Il livello di intensità sonora è indicato come β ed è dato in decibel da:
β = 10 log (I / Io)
Dove io è l'intensità del suono e ioo è un livello di riferimento che viene preso come soglia dell'udito in 1 x 10-12 W / mDue.
Esperimenti pratici per bambini
I bambini possono imparare molto sulle onde meccaniche divertendosi. Ecco alcuni semplici esperimenti per vedere come le onde trasmettono energia, che può essere sfruttata.
-Esperimento 1: interfono
Materiali
- 2 bicchieri di plastica la cui altezza è notevolmente maggiore del diametro.
- Tra 5 e 10 metri di filo forte.
Mettere in pratica
Forare la base degli occhiali per farvi passare il filo e fissarlo con un nodo a ciascuna estremità in modo che il filo non scivoli.
- Ogni giocatore prende un bicchiere e si allontana in linea retta, assicurandosi che il filo sia teso.
- Uno dei giocatori usa il suo vetro come microfono e parla al suo partner, che ovviamente deve avvicinarsi il bicchiere all'orecchio per ascoltare. Non c'è bisogno di gridare.
L'ascoltatore noterà immediatamente che il suono della voce del suo partner viene trasmesso attraverso il filo teso. Se il filo non è teso, la voce del tuo amico non verrà ascoltata chiaramente. Né sentirai nulla se metti il filo direttamente nell'orecchio, il vetro è necessario per ascoltare.
Spiegazione
Sappiamo dalle sezioni precedenti che la tensione nella corda influisce sulla velocità dell'onda. La trasmissione dipende anche dal materiale e dal diametro dei vasi. Quando il partner parla, l'energia della sua voce viene trasmessa all'aria (onda longitudinale), da lì al fondo del bicchiere e poi come un'onda trasversale attraverso il filo.
Il filo trasmette l'onda al fondo del vaso dell'ascoltatore, che vibra. Questa vibrazione viene trasmessa all'aria ed è percepita dal timpano e interpretata dal cervello..
-Esperimento 2: osservazione delle onde
Mettere in pratica
Su un tavolo o su una superficie piana a slinky, la molla elicoidale flessibile con cui si possono formare vari tipi di onda.

Onde longitudinali
Le estremità sono tenute, una per mano. Quindi un piccolo impulso orizzontale viene applicato ad una delle estremità e si osserva come un impulso si propaga lungo la molla.
Puoi anche posizionare un'estremità del file slinky fissato a un supporto o chiedere a un partner di tenerlo, allungandolo abbastanza. In questo modo si ha più tempo per osservare come le compressioni e le espansioni si susseguono propagandosi rapidamente da un'estremità all'altra della molla, come descritto nei paragrafi precedenti..
Onde trasversali
Lo slinky è anche tenuto a una delle sue estremità, allungandolo abbastanza. L'estremità libera viene leggermente scossa scuotendola su e giù. Si osserva che l'impulso sinusoidale viaggia lungo la molla e ritorna.
Riferimenti
- Giancoli, D. (2006). Fisica: principi con applicazioni. Sesta edizione. Prentice Hall. 308- 336.
- Hewitt, Paul. (2012). Scienze fisiche concettuali. Quinta edizione. Pearson. 239 - 244.
- Rex, A. (2011). Fondamenti di fisica. Pearson. 263-273.


Nessun utente ha ancora commentato questo articolo.