
Numeri trascendenti cosa sono, formule, esempi, esercizi
Il numeri trascendenti sono quelli che non possono essere ottenuti come risultato di un'equazione polinomiale. L'opposto di un numero trascendente è a numero algebrico, che sono soluzioni di un'equazione polinomiale del tipo:
pern Xn + pern-1 Xn-1 +... + ADue XDue + per1 x + a0 = 0
Dove i coefficienti an, pern-1,… perDue, per1, per0 sono numeri razionali, chiamati coefficienti del polinomio. Se un numero x è una soluzione all'equazione precedente, allora quel numero non è trascendente.

Analizzeremo alcuni numeri e vedremo se sono trascendenti o meno:
a) 3 non è trascendente perché è una soluzione di x - 3 = 0.
b) -2 non può essere trascendente perché è una soluzione di x + 2 = 0.
c) ⅓ è una soluzione di 3x - 1 = 0
d) Una soluzione dell'equazione xDue - 2x + 1 = 0 è √2 -1, quindi quel numero per definizione non è trascendente.
e) Nessuno dei due è √2 perché è il risultato dell'equazione xDue - 2 = 0. Il quadrato √2 dà il risultato 2, che sottratto da 2 è uguale a zero. Quindi √2 è un numero irrazionale ma non è trascendente.
Indice articolo
- 1 Cosa sono i numeri trascendenti?
- 1.1 Il numero π
- 1.2 Il numero e
- 2 Formule in cui appare il numero trascendente π
- 2.1 Il perimetro della circonferenza
- 2.2 Area di un cerchio
- 2.3 Superficie di una sfera
- 2.4 Volume della sfera
- 3 esercizi
- 3.1 - Esercizio 1
- 3.2 - Esercizio 2
- 4 Riferimenti
Cosa sono i numeri trascendenti?
Il problema è che non esiste una regola generale per ottenerli (più avanti diremo un modo), ma alcuni dei più famosi sono il numero pi e il Numero Neper, indicato rispettivamente da: π Y e.
Il numero π
Il numero π Appare naturalmente osservando che il quoziente matematico tra il perimetro P di un cerchio e il suo diametro D, indipendentemente dal fatto che si tratti di un cerchio piccolo o grande, dà sempre lo stesso numero, chiamato pi:
π = P / D ≈ 3,14159 ...
Ciò significa che se si prende come unità di misura il diametro della circonferenza, per tutte, grandi o piccole, il perimetro sarà sempre P = 3.14… = π, come si può vedere nell'animazione della figura 2.
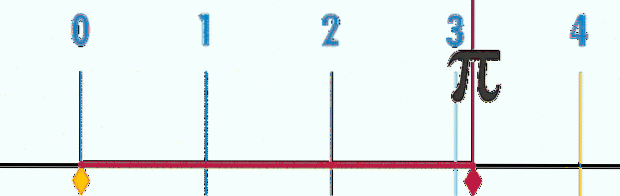
Per determinare più decimali, è necessario misurare P e D con maggiore precisione e quindi calcolare il quoziente, che è stato fatto matematicamente. La linea di fondo è che i decimali del quoziente non hanno fine e non si ripetono mai, quindi il numero π oltre ad essere trascendente, lo è anche irrazionale.
Un numero irrazionale è un numero che non può essere espresso come divisione di due numeri interi.
È noto che ogni numero trascendente è irrazionale, ma non è vero che tutti i numeri irrazionali sono trascendenti. Ad esempio √2 è irrazionale, ma non è trascendente.
Il numero e
Il numero trascendente e è la base dei logaritmi naturali e la sua approssimazione decimale è:
e ≈ 2,718281828459045235360… .
Se volessi scrivere il numero e esattamente, sarebbe necessario scrivere decimali infiniti, perché ogni numero trascendente è irrazionale, come detto prima.
Le prime dieci cifre di e sono facili da ricordare:
2,7 1828 1828 e sebbene sembri seguire uno schema ripetitivo, ciò non si ottiene in decimali di ordine maggiore di nove.
Una definizione più formale di e è il prossimo:
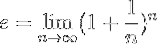
Il che significa che il valore esatto di e si ottiene eseguendo l'operazione indicata in questa formula, quando il numero naturale n tende all'infinito.
Questo spiega perché possiamo ottenere solo approssimazioni di e, poiché non importa quanto grande sia il numero n, sarà sempre possibile trovare a n più alto.
Cerchiamo da soli alcune approssimazioni:
-Quando n = 100 allora (1 + 1/100)100 = 2.70481 che difficilmente coincide nel primo decimale con il valore “vero” di e.
-Se scegli n = 10.000 hai (1 + 1 / 10.000)10.000 = 2,71815 che corrisponde al valore "esatto" di e nelle prime tre cifre decimali.
Questo processo dovrebbe essere seguito all'infinito per ottenere il valore "vero" di e. Non credo che abbiamo tempo per farlo, ma proviamone un altro:
Usiamo n = 100.000:
(1 + 1 / 100.000)100.000 = 2,7182682372
Questo ha solo quattro cifre decimali che corrispondono al valore considerato esatto.
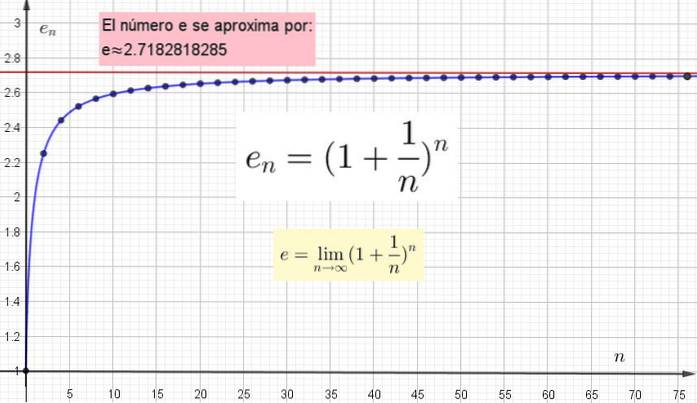
L'importante è capire che maggiore è il valore di n scelto per calcolare en, più si avvicina al valore reale. Ma quel valore vero si avrà solo quando n è infinito.
Altri numeri importanti
Oltre a questi numeri famosi ci sono altri numeri trascendenti, ad esempio:
- Due√2
Ogni numero algebrico, diverso da 0 o 1, elevato a un esponente irrazionale sarà un numero trascendente.
-Il numero Champernowne in base 10:
C_10 = 0,123456789101112131415161718192021 ... .
-Il numero Champernowne in base 2:
C_2 = 0,1101110010110111… .
-Il numero gamma γ o costante di Eulero-Mascheroni:
γ ≈ 0,577 215 664901532860606
Che si ottiene eseguendo il seguente calcolo:
γ ≈ 1 + ½ + ⅓ + ¼ +… + 1 / n - ln (n)
quando n essere molto molto grande. Per avere il valore esatto del numero Gamma, è necessario eseguire il calcolo con n infinito. Qualcosa di simile a quello che abbiamo fatto sopra.
E ci sono molti altri numeri trascendenti. Il grande matematico Georg Cantor, nato in Russia e vissuto tra il 1845 e il 1918, ha dimostrato che l'insieme dei numeri trascendenti è molto maggiore dell'insieme dei numeri algebrici.
Formule in cui appare il numero trascendente π
Il perimetro della circonferenza
P = π D = 2 π R, dove P è il perimetro, D il diametro e R il raggio della circonferenza. Va ricordato che:
-Il diametro della circonferenza è il segmento più lungo che unisce due punti della stessa e che passa sempre per il suo centro,
-Il raggio è la metà del diametro ed è il segmento che va dal centro al bordo.
Area di un cerchio
A = π RDue = ¼ π DDue
Superficie di una sfera
S = 4 π RDue.
Sì. Anche se può non sembrare, la superficie di una sfera è uguale a quella di quattro cerchi dello stesso raggio della sfera..
Volume della sfera
V = 4/3 π R3
Formazione
- Esercizio 1
La pizzeria “EXÓTICA” vende pizze di tre diametri: piccola 30 cm, media 37 cm e grande 45 cm. Un bambino ha molta fame e si è accorto che due pizze piccole costano come una grande. Cosa sarà meglio per lui, compra due pizze piccole o una grande?

Soluzione
Maggiore è la superficie, maggiore sarà la quantità di pizza, per questo motivo verrà calcolata la superficie di una pizza grande e confrontata con quella di due pizze piccole:
Ampia area pizza = ¼ π DDue = ¼ ⋅3,1416⋅45Due = 1590,44 cmDue
Piccola area pizza = ¼ π dDue = ¼ ⋅3,1416⋅30Due = 706,86 cmDue
Quindi due pizzette avranno una superficie di
2 x 706,86 = 1413,72 cmDue .
È chiaro: avrai più pizze acquistando una sola grande che due piccole.
- Esercizio 2
La pizzeria “EXÓTICA” vende anche una pizza semisferica con raggio di 30 cm allo stesso prezzo di una pizza di forma rettangolare con un lato di 30 x 40 cm. Quale sceglieresti?

Soluzione
Come accennato nella sezione precedente, la superficie di una sfera è quattro volte quella di un cerchio dello stesso diametro, quindi un emisfero di 30 cm di diametro avrà:
Pizza semisferica 12 '': 1413,72 cmDue (due volte una circolare dello stesso diametro)
Pizza rettangolare: (30 cm) x (40 cm) = 1200 cmDue .
La pizza semisferica ha una superficie più ampia.
Riferimenti
- Fernández J. Il numero e. Origine e curiosità. Estratto da: soymatematicas.com
- Goditi la matematica. Il numero di Eulero. Estratto da: gustolasmatematicas.com.
- Figuera, J. 2000. Matematica 1st. Diversificato. Edizioni CO-BO.
- García, M. Il numero e nel calcolo elementare. Estratto da: matematica.ciens.ucv.ve.
- Wikipedia. Numero PI. Estratto da: wikipedia.com
- Wikipedia. Numeri trascendenti. Estratto da: wikipedia.com


Nessun utente ha ancora commentato questo articolo.