
Angoli supplementari cosa sono, calcoli, esempi, esercizi
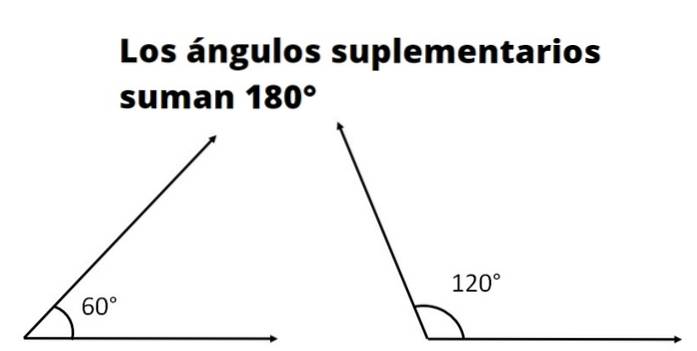
Due o più lo sono angoli supplementari se la somma delle sue misure corrisponde alla misura di un angolo retto. La misura di un angolo retto, chiamato anche angolo piano, in gradi è 180º e in radianti è π.
Ad esempio, troviamo che i tre angoli interni di un triangolo sono supplementari, poiché la somma delle loro misure è 180º. Tre angoli sono mostrati nella Figura 1. Da quanto sopra segue che α e β sono supplementari, poiché sono adiacenti e la loro somma completa un angolo retto.
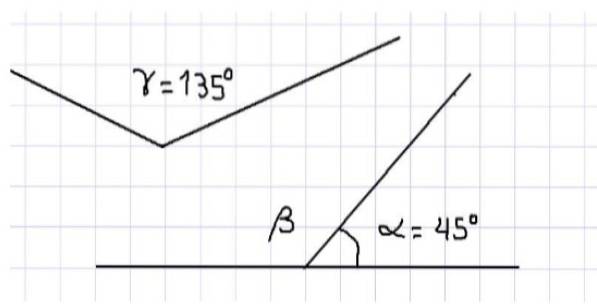
Sempre nella stessa figura abbiamo gli angoli α e γ che sono anche supplementari, perché la somma delle loro misure è uguale alla misura di un angolo piano, cioè 180º. Non si può dire che gli angoli β e γ siano supplementari perché, essendo entrambi ottusi, le loro misure sono maggiori di 90º e quindi la loro somma supera 180º.
D'altra parte, si può affermare che la misura dell'angolo β è uguale alla misura dell'angolo γ, poiché se β è supplementare a α e γ è supplementare a α, allora β = γ = 135º.
Indice articolo
- 1 Esempi
- 1.1 Esempio A
- 1.2 Esempio B
- 1.3 Esempio C
- 1.4 Esempio D
- 1.5 Esempio E
- 1.6 Esempio F
- 2 esercizi
- 2.1 - Esercizio I
- 2.2 - Esercizio II
- 2.3 - Esercizio III
- 3 Angoli supplementari in due paralleli tagliati da una secante
- 3.1 - Esercizio IV
- 4 Riferimenti
Esempi
Negli esempi seguenti, viene chiesto di trovare gli angoli sconosciuti, indicati con punti interrogativi nella figura 2. Si va dagli esempi più semplici ad alcuni un po 'più elaborati che il lettore dovrebbe stare più attento.
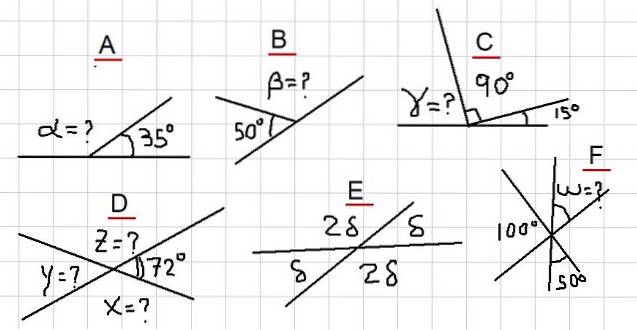
Esempio A
Nella figura abbiamo che gli angoli adiacenti α e 35º si sommano ad un angolo piano. Cioè, α + 35º = 180º e quindi è vero che: α = 180º- 35º = 145º.
Esempio B
Poiché β è supplementare con l'angolo di 50º, ne consegue che β = 180º - 50º = 130º.
Esempio C
Dalla figura 2C si osserva la seguente somma: γ + 90º + 15º = 180º. Cioè, γ è supplementare con l'angolo 105º = 90º + 15º. Si conclude quindi che:
γ = 180º- 105º = 75º
Esempio D
Poiché X è supplementare a 72º, ne segue che X = 180º - 72º = 108º. Inoltre Y è supplementare con X, quindi Y = 180º - 108º = 72º.
Infine Z è supplementare con 72º, quindi Z = 180º - 72º = 108º.
Esempio E
Gli angoli δ e 2δ sono supplementari, quindi δ + 2δ = 180º. Il che significa che 3δ = 180º, e questo a sua volta ci permette di scrivere: δ = 180º / 3 = 60º.
Esempio F
Se chiamiamo l'angolo tra 100º e 50º U, allora U è supplementare a loro, perché si osserva che la loro somma completa un angolo piano.
Ne consegue immediatamente che U = 150º. Poiché U è opposta per il vertice a W, allora W = U = 150º.
Formazione
Di seguito vengono proposti tre esercizi, in tutti si deve trovare il valore degli angoli A e B in gradi, in modo da soddisfare le relazioni mostrate in figura 3. Il concetto di angoli supplementari viene utilizzato per risolverli tutti..
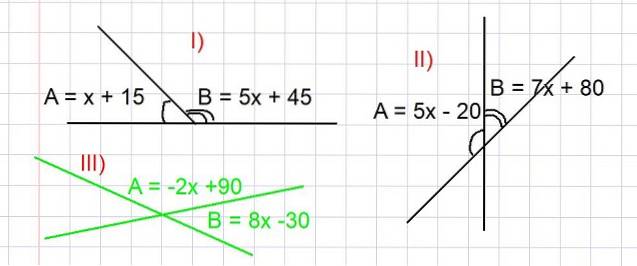
- Esercizio I.
Determina i valori degli angoli A e B dalla parte I) della Figura 3.
Soluzione
A e B sono supplementari, da cui abbiamo che A + B = 180 gradi, quindi l'espressione di A e B viene sostituita in funzione di x, come appare nell'immagine:
(x + 15) + (5x + 45) = 180
Si ottiene un'equazione lineare del primo ordine. Per risolverlo, i termini vengono raggruppati immediatamente:
6 x + 60 = 180
Dividendo entrambi i membri per 6 abbiamo:
x + 10 = 30
E alla fine risolvendo, ne consegue che x vale 20º.
Ora dobbiamo inserire il valore di x per trovare gli angoli richiesti. Quindi, l'angolo A è: A = 20 +15 = 35º.
E da parte sua, l'angolo B è B = 5 * 20 + 45 = 145º.
- Esercizio II
Trova i valori degli angoli A e B dalla parte II) della Figura 3.
Soluzione
Poiché A e B sono angoli supplementari, abbiamo che A + B = 180 gradi. Sostituendo l'espressione per A e B in funzione di x data nella parte II) della figura 3, abbiamo:
(-2x + 90) + (8x - 30) = 180
Ancora una volta si ottiene un'equazione di primo grado, per la quale i termini devono essere opportunamente raggruppati:
6 x + 60 = 180
Dividendo entrambi i membri per 6 abbiamo:
x + 10 = 30
Da cui segue che x vale 20º.
In altre parole, l'angolo A = -2 * 20 + 90 = 50º. Mentre l'angolo B = 8 * 20 - 30 = 130º.
- Esercizio III
Determina i valori degli angoli A e B dalla parte III) della figura 3 (in colore verde).
Soluzione
Poiché A e B sono angoli supplementari, abbiamo che A + B = 180 gradi. Dobbiamo sostituire l'espressione per A e B in funzione di x data in figura 3, da cui abbiamo:
(5x - 20) + (7x + 80) = 180
12 x + 60 = 180
Dividendo entrambi i membri per 12 per risolvere il valore di x, abbiamo:
x + 5 = 15
Infine si trova che x vale 10 gradi.
Ora procediamo con la sostituzione per trovare l'angolo A: A = 5 * 10-20 = 30º. E per l'angolo B: B = 7 * 10 + 80 = 150º
Angoli supplementari in due paralleli tagliati da una secante
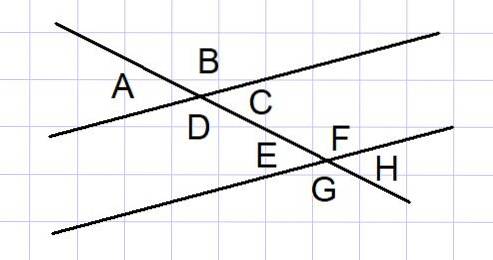
Due linee parallele tagliate da una secante sono una costruzione geometrica comune in alcuni problemi. Tra tali linee, vengono formati 8 angoli come mostrato nella figura 4.
Di questi 8 angoli, alcune coppie di angoli sono supplementari, che elenchiamo di seguito:
- Gli angoli esterni A e B e gli angoli esterni G e H
- Gli angoli interni D e C e gli angoli interni E e F
- Gli angoli esterni A e G e gli angoli esterni B e H
- Gli angoli interni D ed E e gli interni C e F
Per completezza, vengono anche denominati gli angoli uguali tra loro:
- Le alterne interne: D = F e C = E
- Le alterne esterne: A = H e B = G
- Quelli corrispondenti: A = E e C = H
- Opposti per vertice A = C ed E = H
- Quelli corrispondenti: B = F e D = G
- Opposti per vertice B = D e F = G
- Esercizio IV
Facendo riferimento alla Figura 4, che mostra gli angoli tra due rette parallele tagliate da una secante, determinare il valore di tutti gli angoli in radianti, sapendo che l'angolo A = π / 6 radianti.
Soluzione
A e B sono angoli esterni supplementari quindi B = π - A = π - π / 6 = 5π / 6
A = E = C = H = π / 6
B = F = D = G = 5π / 6
Riferimenti
- Baldor, J. A. 1973. Plane and Space Geometry. Centro culturale americano.
- Leggi e formule matematiche. Sistemi di misura angolari. Estratto da: ingemecanica.com.
- Wentworth, G. Plane Geometry. Estratto da: gutenberg.org.
- Wikipedia. Angoli supplementari. Estratto da: es.wikipedia.com
- Wikipedia. Trasportatore. Estratto da: es.wikipedia.com
- Zapata F. Goniómetro: storia, parti, operazione. Estratto da: lifeder.com



Nessun utente ha ancora commentato questo articolo.