
Angoli nei tipi di circonferenza, proprietà, esercizi risolti
Chiamato angoli di circonferenza quelli in cui alcuni dei suoi elementi sono o si intersecano in una data circonferenza. Tra questi ci sono i seguenti:
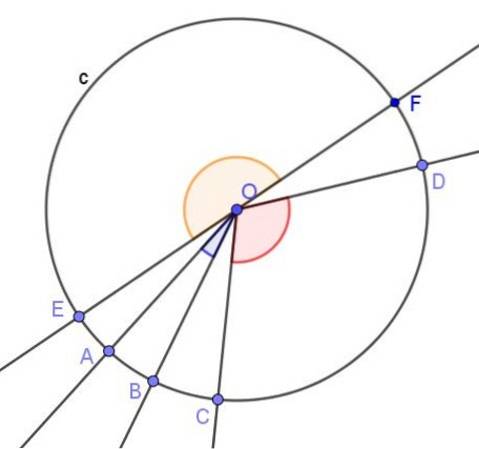
1.- Il angolo centrale, il cui vertice è al centro della circonferenza ed i suoi lati sono secanti ad essa, come si vede nell'immagine seguente:

2.- Il angolo inscritto, il cui vertice è sulla circonferenza ed i suoi lati sono secanti o tangenti alla circonferenza.
3.- Angolo esterno, il cui vertice è esterno alla circonferenza ma i suoi lati sono secanti o tangenti alla circonferenza.
4.- Il angolo interno, con il vertice interno alla circonferenza ed i suoi lati secanti ad essa.
Tutti questi angoli hanno determinate relazioni tra loro e questo ci porta a proprietà importanti tra gli angoli appartenenti a un dato cerchio.
Indice articolo
- 1 Proprietà
- 1.1 - Angolo centrale
- 1.2 - Angolo inscritto
- 1.3 - Angolo esterno
- 1.4 - Angolo interno
- 2 Esercizi risolti
- 2.1 - Esercizio 1
- 2.2 - Esercizio 2
- 3 Riferimenti
Proprietà
- Angolo centrale
L'angolo centrale è definito come quello il cui vertice è al centro della circonferenza ei suoi lati intersecano la circonferenza.
La misura in radianti di un angolo centrale è il quoziente tra l'arco sottendente, cioè l'arco di circonferenza tra i lati dell'angolo, e il raggio della circonferenza.
Se la circonferenza è unitaria, cioè di raggio 1, allora la misura dell'angolo centrale è la lunghezza dell'arco, che corrisponde al numero di radianti.
Se vuoi la misura dell'angolo centrale in gradi, moltiplica la misura in radianti per il fattore 180º / π.
Gli strumenti di misura dell'angolo, come il goniometro e il goniometro, utilizzano sempre un angolo centrale e la lunghezza dell'arco sotteso.
Sono calibrati in gradi sessagesimali, il che significa che ogni volta che con essi si misura un angolo, sullo sfondo si misura la lunghezza dell'arco sotteso dall'angolo centrale.
Proprietà
La misura di un angolo centrale in radianti è uguale alla lunghezza dell'arco sottendente o di intercettazione divisa per la lunghezza del raggio.
- Angolo inscritto
L'angolo inscritto di un cerchio è quello che ha il suo vertice sulla circonferenza ei suoi raggi sono secanti o tangenti ad esso..
Le sue proprietà sono:
Proprietà
-L'angolo inscritto è convesso o piano.
-Quando un angolo inscritto interseca lo stesso arco dell'angolo centrale, la misura del primo angolo sarà la metà di quella del secondo..
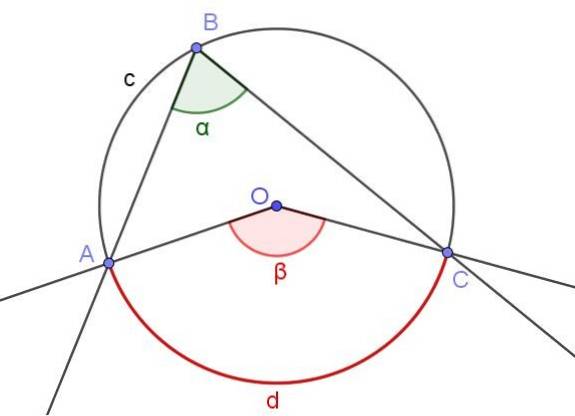
La figura 3 mostra due angoli ∠ABC e ∠AOC che intersecano lo stesso arco di circonferenza A⌒C.
Se la misura dell'angolo inscritto è α, allora la misura β dell'angolo centrale è il doppio della misura dell'angolo inscritto (β = 2 α) perché entrambi sottendono lo stesso arco di misura d.
- Angolo esterno
È l'angolo il cui vertice è esterno alla circonferenza e ciascuno dei suoi lati taglia la circonferenza in uno o più punti.
Proprietà
-La sua misura è pari alla mezza differenza (o differenza divisa per 2) degli angoli centrali che intercettano gli stessi archi.
Per garantire che la misura sia positiva, la semidifferenza deve sempre essere quella dell'angolo centrale più grande meno la misura dell'angolo centrale più piccolo, come illustrato nella figura seguente.
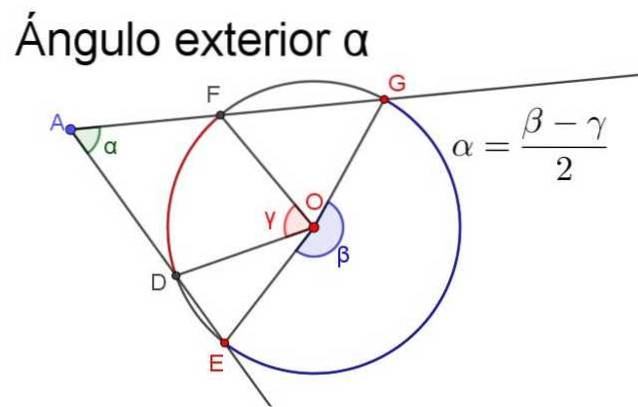
- Angolo interno
L'angolo interno è quello il cui vertice è all'interno della circonferenza ei suoi lati intersecano la circonferenza.
Proprietà
La sua misura è uguale alla semi-somma dell'angolo centrale che sottende lo stesso arco, più l'angolo centrale che sottende lo stesso arco del suo angolo di estensione (è l'angolo interno formato dai raggi complementari a quelli dell'angolo interno originale ).
La figura seguente illustra e chiarisce la proprietà dell'angolo interno.
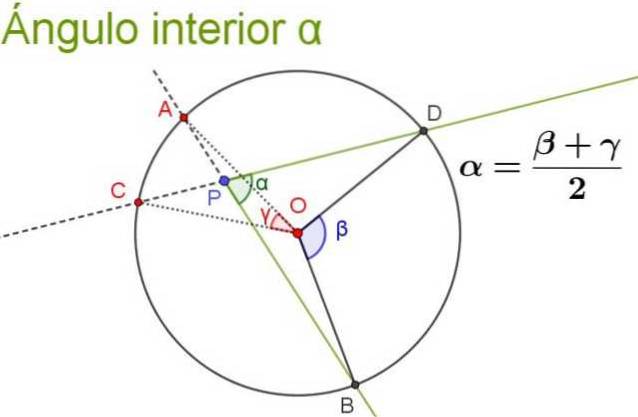
Esercizi risolti
- Esercizio 1
Supponiamo che un angolo inscritto in cui uno dei suoi lati passi per il centro del cerchio, come mostrato nella Figura 6. Il raggio del cerchio è OA = 3 cm e l'arco d ha una lunghezza di π / 2 cm. Determina il valore degli angoli α e β.
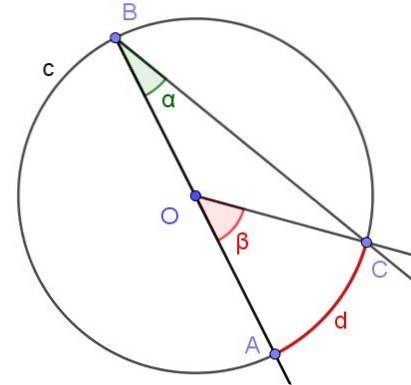
Soluzione
In questo caso, si forma il triangolo isoscele COB, poiché [OC] = [OB]. In un triangolo isoscele gli angoli adiacenti alla base sono uguali, quindi ∠BCO = ∠ABC = α. D'altra parte ∠COB = 180º - β. Considerando la somma degli angoli interni del triangolo COB, abbiamo:
α + α + (180º - β) = 180º
Da cui segue che 2 α = β, ovvero quanto è equivalente α = β / 2, con cui si conferma la proprietà (3) del paragrafo precedente, che la misura dell'angolo inscritto è la metà dell'angolo centrale, quando entrambi gli angoli sottendi lo stesso accordo [AC].
Procediamo ora alla determinazione dei valori numerici: l'angolo β è centrale e la sua misura in radianti è il quoziente tra l'arco d e il raggio r = OA, quindi la sua misura è:
β = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30º.
D'altra parte, era già stato affermato che α = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15º.
- Esercizio 2
Nella figura 7 gli angoli α1 e βDue hanno la stessa misura. Inoltre, l'angolo β1 misura 60º. Determina gli angoli β e α.
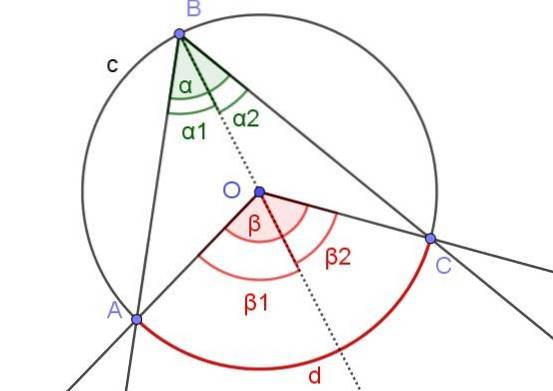
Soluzione
In questo caso abbiamo un angolo inscritto ∠ABC in cui il centro O della circonferenza è all'interno dell'angolo.
A causa della proprietà (3) abbiamo αDue = βDue / 2 e α1 = β1 /Due. Che cosa:
α = α1 + αDue e β = β1 + βDue
Pertanto, ne consegue che:
α = α1 + αDue = β1 / 2 + βDue / 2 = (β1 + βDue) / 2 = β / 2.
Cioè, secondo le proprietà:
α = β / 2
Dato che ci viene detto che β1 = 60º allora:
α1 = β1 / 2 = 60º / 2 = 30º.
Ci dicono anche che α1 = βDue quindi ne consegue che:
βDue = 30º.
L'angolo β risulta:
β1 + βDue = 60º + 30º = 90º.
E poiché α = β / 2, allora:
α = 90º / 2 = 45º.
In conclusione:
β = 90º e α = 45º.
Riferimenti
- Baldor, A. 1973. Geometria e trigonometria. Casa editrice culturale centroamericana.
- E. A. 2003. Elementi di geometria: con esercizi e geometria della bussola. Università di Medellin.
- Geometria 1 ° ESO. Angoli sulla circonferenza. Recupero da: edu.xunta.es.
- Tutta la scienza. Risolti problemi di angoli nella circonferenza. Estratto da: francesphysics.blogspot.com
- Wikipedia. Angolo inscritto. Estratto da: es.wikipedia.com



Nessun utente ha ancora commentato questo articolo.