
Esempi di angoli interni ed esterni coniugati, esercizi
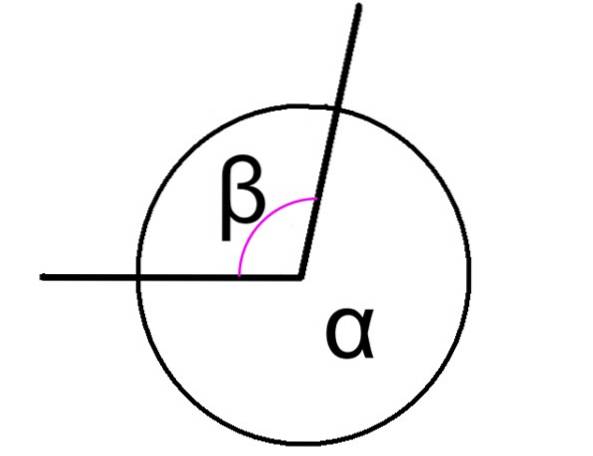
Il angoli coniugati Sono quelli che, sommati, danno come risultato 360 °, indipendentemente dal fatto che questi angoli siano adiacenti o meno. Nella figura 1 sono mostrati due angoli coniugati, indicati come α e β.
In questo caso, gli angoli α e β nella figura hanno un vertice comune ed i loro lati sono comuni, quindi sono adiacenti. La relazione tra loro è espressa come segue:
α + β = 360º
Consideriamo invece ora due rette parallele tagliate da una secante, la cui disposizione è mostrata di seguito:
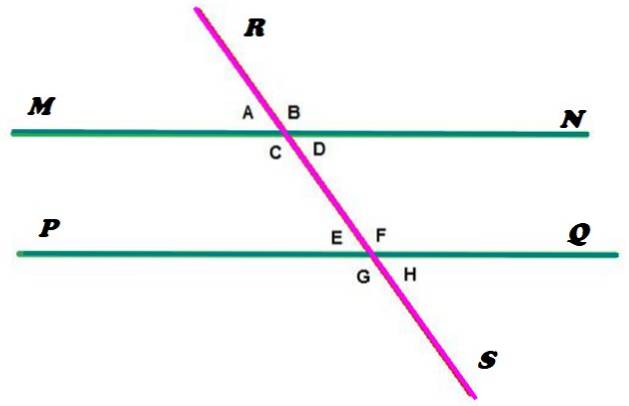
Le linee MN e PQ sono parallele, mentre la linea RS è secante, intersecando le parallele in due punti. Come si può vedere, questa configurazione determina la formazione di 8 angoli, che sono stati indicati con lettere minuscole.
Ebbene, secondo la definizione data all'inizio, gli angoli a, b, ce d sono coniugati. E allo stesso modo e, f, geh sono, poiché entrambi i casi sono veri:
a + b + c + d = 360º
Y
e + f + g + h = 360º
Per questa configurazione si coniugano due angoli se sono dallo stesso lato rispetto alla linea secante RS ed entrambi sono interni o esterni. Nel primo caso parliamo di angoli coniugati interni, mentre nella seconda sono angoli coniugati esterni.
Indice articolo
- 1 Esempi
- 2 Angoli interni di un quadrilatero
- 2.1 Esempi
- 3 esercizi
- 3.1 - Esercizio 1
- 3.2 - Esercizio 2
- 4 Riferimenti
Esempi
Nella figura 2, gli angoli esterni sono quelli che sono al di fuori della regione delimitata dalle linee MN e PQ, sono gli angoli A, B, G e H.Mentre gli angoli che si trovano tra le due linee sono C, D, E e F.
Ora è necessario analizzare quali angoli sono a sinistra e quali a destra della secante.
A sinistra di RS ci sono gli angoli A, C, E e G. E a destra ci sono gli angoli B, D, F e H.
Si procede subito alla determinazione delle coppie di angoli coniugati, secondo la definizione data nella sezione precedente:
-A e G, esterni ea sinistra di RS.
-D e F, interni ea destra di RS.
-B e H, esterni ea destra di RS.
-C ed E, interno ea sinistra di RS.
Proprietà degli angoli coniugati tra rette parallele
Gli angoli coniugati tra rette parallele sono supplementari, cioè la loro somma è pari a 180º. In questo modo, per la figura 2 vale quanto segue:
A + G = 180º
D + F = 180º
B + H = 180º
C + E = 180º
Le coppie di angoli corrispondenti per le linee parallele
Sono quelli che si trovano sullo stesso lato della linea secante, non sono adiacenti e uno di essi è interno e l'altro è esterno. È importante visualizzarli, poiché la loro misura è la stessa, perché sono angoli opposti rispetto al vertice.
Tornando alla Figura 2, le coppie di angoli corrispondenti sono identificate come:
-A ed E
-C e G
-B e F
-D e H
Angoli interni di un quadrilatero
I quadrilateri sono poligoni a 4 facce, tra cui il quadrato, il rettangolo, il trapezio, il parallelogramma e il rombo, ad esempio. Indipendentemente dalla loro forma, in ognuno di essi è vero che la somma dei loro angoli interni è di 360º, quindi soddisfano la definizione data all'inizio..
Vediamo alcuni esempi di quadrilateri e come calcolare il valore dei loro angoli interni secondo le informazioni nelle sezioni precedenti:
Esempi
a) Tre angoli di un quadrilatero misurano 75º, 110º e 70º. Quanto dovrebbe misurare l'angolo rimanente?
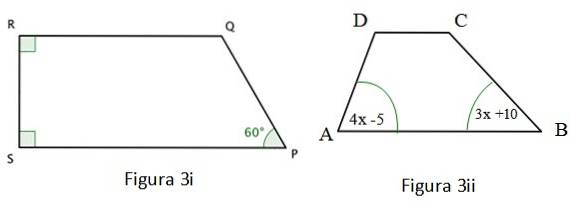
b) Trova il valore dell'angolo ∠Q nella figura 3 i.
c) Calcola la misura dell'angolo ∠A in figura 3 ii.
Soluzione a
Sia α l'angolo mancante, si è accertato che:
α + 75º + 110º + 70º = 360º → α = 105º
Soluzione b
La figura 3i mostrata è un file trapezio e due dei suoi angoli interni sono retti, che sono stati contrassegnati con un quadrato colorato agli angoli. Per questo quadrilatero si verifica quanto segue:
∠R + ∠S + ∠P + ∠Q = 360º; ∠S = ∠R = 90 °; ∠P = 60º
Perciò:
∠ Q = 2 x 90º + 60º = 240º
Soluzione c
Anche il quadrilatero nella figura 3 ii è un trapezio, per il quale vale quanto segue:
∠A + ∠B + ∠C + ∠D = 360º
Perciò:
4x -5 + 3x + 10 +180 = 360
7x + 5 = 180
x = (180-5) / 7
x = 25
Per determinare l'angolo richiesto nell'istruzione, usiamo che ∠A = 4x - 5. Sostituendo il valore di x calcolato in precedenza segue che ∠A = (4 × 25) -5 = 95º
Formazione
- Esercizio 1
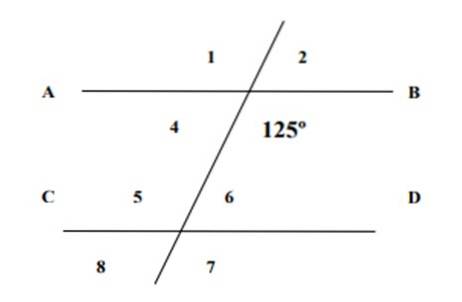
Sapendo che uno degli angoli mostrati è 125º, trova le misure dei 7 angoli rimanenti nella figura seguente e giustifica le risposte.
Soluzione
L'angolo 6 e l'angolo 125º sono coniugati interni, la cui somma è 180º, secondo la proprietà degli angoli coniugati, quindi:
∠6 + 125º = 180º → ∠6 = 180º - 125º = 55º
D'altra parte ∠6 e ∠8 sono angoli opposti dal vertice, la cui misura è la stessa. Pertanto ∠8 misura 55º.
L'angolo ∠1 è anche opposto al vertice a 125º, quindi possiamo affermare che ∠1 = 125º. Possiamo anche fare appello al fatto che le coppie di angoli corrispondenti hanno la stessa misura. Nella figura questi angoli sono:
∠7 = 125 º
∠2 = ∠6 = 55 º
∠1 = ∠5 = 125º
∠4 = ∠8 = 55 º
- Esercizio 2
Trova il valore di x nella figura seguente ei valori di tutti gli angoli:
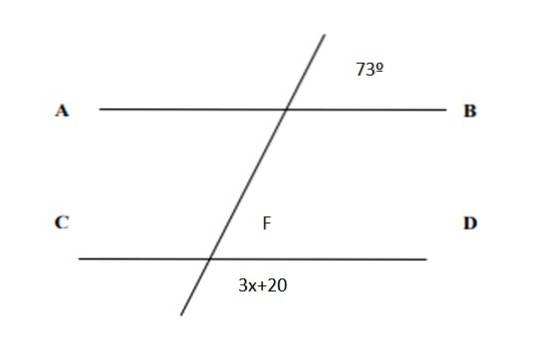
Soluzione
Poiché sono coppie corrispondenti, ne consegue che F = 73º. E d'altra parte la somma delle coppie coniugate è di 180º, quindi:
3x + 20º + 73º = 180º
3x = 180º - 73º -20º = 87
Infine il valore di x è:
x = 87/3 = 29
Come per tutti gli angoli, sono elencati nella figura seguente:
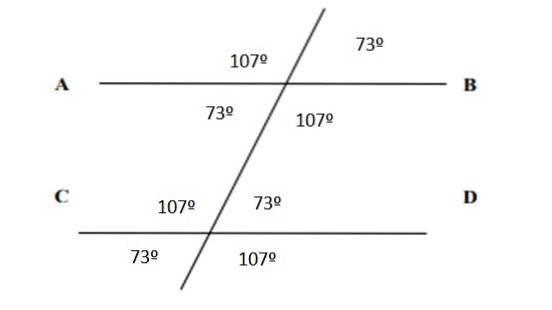
Riferimenti
- Gruppi di angoli. Spiegazione degli angoli complementari, supplementari ed esemplificativi. Estratto da: thisiget.com/
- Baldor, A. 1983. Geometria e trigonometria del piano e dello spazio. Patria Cultural Group.
- Corral, M. Mathematics LibreTexts: Angles. Recupero da: math.libretexts.org.
- Mathmania. Classificare e costruire angoli in base alla loro misurazione. Recupero da: matematica.com/
- Wentworth, G. Plane Geometry. Estratto da: gutenberg.org.
- Wikipedia. Angoli coniugati. Estratto da: es.wikipedia.org.


Nessun utente ha ancora commentato questo articolo.