
Metodo Eulero a cosa serve, procedura ed esercizi
Il Metodo di Eulero è la più elementare e semplice delle procedure utilizzate per trovare soluzioni numeriche approssimative a un'equazione differenziale ordinaria del primo ordine, a condizione che la sua condizione iniziale sia nota.
Un'equazione differenziale ordinaria (ODE) è l'equazione che mette in relazione una funzione sconosciuta di una singola variabile indipendente con le sue derivate.
Se la derivata più grande che appare nell'equazione è di grado uno, allora è un'equazione differenziale ordinaria di primo grado.
Il modo più generale per scrivere un'equazione di primo grado è:

x = x0
y = y0
Indice articolo
- 1 Qual è il metodo di Eulero?
- 2 Esercizi risolti
- 2.1 Esercizio 1
- 2.2 Esercizio 2
- 2.3 Esercizio 3
- 3 Dinamica di Newton e metodo di Eulero
- 3.1 Esercizio 4
- 4 Esercizi proposti per casa
- 4.1 Esercizio 1
- 4.2 Esercizio 2
- 5 Riferimenti
Qual è il metodo di Eulero?
L'idea del metodo di Eulero è trovare una soluzione numerica all'equazione differenziale nell'intervallo tra X0 e XF .
Innanzitutto, l'intervallo è discretizzato in n + 1 punti:
X0, X1, XDue, X3..., Xn
Che si ottengono così:
Xio= x0+ih
Dove h è la larghezza o il passo dei sottointervalli:

Con la condizione iniziale, poi, è anche possibile conoscere la derivata all'inizio:
y '(xo) = f (xo, Yo)
Questa derivata rappresenta la pendenza della tangente alla curva della funzione y (x) precisamente nel punto:
Ao = (xo, Yo)
Quindi una previsione approssimativa del valore della funzione y (x) viene effettuata nel punto seguente:
y (x1) ≈ e1
Y1 = Yo +(X1- Xo) f (xo, Yo) = eo + h f (xo, Yo)
Si è quindi ottenuto il successivo punto approssimativo della soluzione, che corrisponderebbe a:
PER1 = (x1, Y1)
La procedura viene ripetuta per ottenere i punti successivi
PERDue, PER3..., Xn
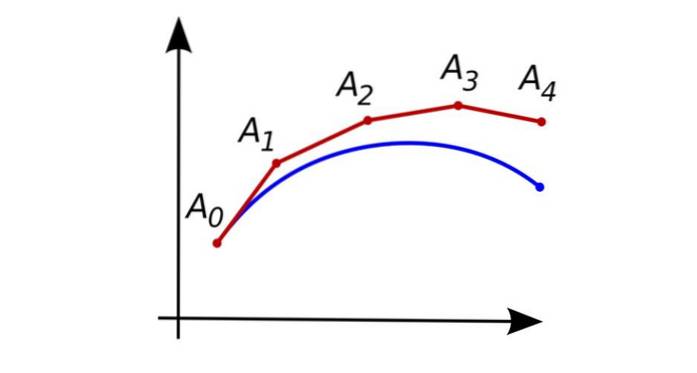
Nella figura mostrata all'inizio, la curva blu rappresenta la soluzione esatta dell'equazione differenziale, e quella rossa rappresenta i successivi punti approssimativi ottenuti con la procedura di Eulero.
Esercizi risolti
Esercizio 1
io) Sia l'equazione differenziale:

Con la condizione iniziale x = a = 0; Yper= 1
Usando il metodo di Eulero, ottieni una soluzione approssimativa di Y nella coordinata X = b = 0,5, suddividendo l'intervallo [a, b] in n = 5 parti.
Soluzione

I risultati numerici sono riassunti come segue:

Da dove si conclude che la soluzione Y per il valore 0,5 è 1,4851.
Nota: per eseguire i calcoli, Studio Smath, libero di usare il programma gratuito.
Esercizio 2
II) Continuando con l'equazione differenziale dell'esercizio I), trova la soluzione esatta e confrontala con il risultato ottenuto con il metodo di Eulero. Trova l'errore o la differenza tra il risultato esatto e quello approssimativo.
Soluzione

La soluzione esatta non è molto difficile da trovare. La derivata della funzione sin (x) è nota per essere la funzione cos (x). Pertanto la soluzione y (x) sarà:
y (x) = sin x + C
Affinché la condizione iniziale sia soddisfatta e (0) = 1, la costante C deve essere uguale a 1. Il risultato esatto viene quindi confrontato con quello approssimativo:
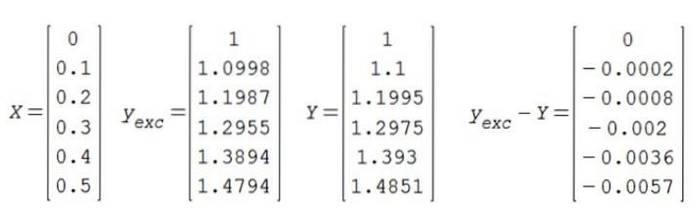
Si conclude che nell'intervallo calcolato, l'approssimazione ha tre cifre significative di precisione.
Esercizio 3
III) Considera l'equazione differenziale e le sue condizioni iniziali fornite di seguito:
y '(x) = - yDue
Con la condizione iniziale x0 = 0; Y0 = 1
Usa il metodo di Eulero per trovare valori approssimativi della soluzione y (x) nell'intervallo x = [0, 1,5]. Usa il passaggio h = 0,1.
Soluzione
Il metodo di Eulero è molto adatto per essere utilizzato con un foglio di calcolo. In questo caso useremo il foglio di calcolo di geogebra, un programma gratuito e gratuito.
Il foglio di calcolo nella figura mostra tre colonne (A, B, C) la prima è la variabile X , la seconda colonna rappresenta la variabile Y, e la terza colonna la derivata Y '.
La riga 2 contiene i valori iniziali di X, Y, Y ' .
Il passo di valore 0.1 è stato inserito nella cella della posizione assoluta ($ D $ 4).
Il valore iniziale di y0 è nella cella B2 e y1 è nella cella B3. Per calcolare y1 si usa la formula:
Y1 = Yo +(X1- Xo) f (xo, Yo) = eo + h f (xo, Yo)
Questa formula del foglio di calcolo sarebbe il numero B3: = B2 + $ D $ 4 * C3.
Allo stesso modo y2 sarebbe nella cella B4 e la sua formula è mostrata nella figura seguente:
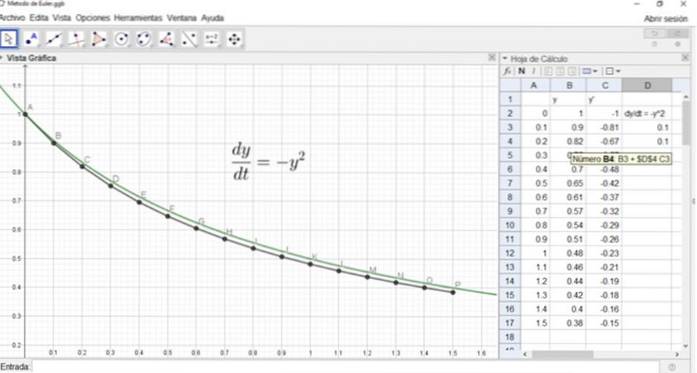
La figura mostra anche il grafico della soluzione esatta e i punti A, B, ..., P della soluzione approssimativa con il metodo di Eulero.
Dinamica newtoniana e metodo di Eulero
La dinamica classica è stata sviluppata da Isaac Newton (1643-1727). La motivazione originale di Leonard Euler (1707-1783) a sviluppare il suo metodo, era proprio quella di risolvere l'equazione della seconda legge di Newton in varie situazioni fisiche.
La seconda legge di Newton è solitamente espressa come un'equazione differenziale di secondo grado:

Dove X rappresenta la posizione di un oggetto nell'istante t. Detto oggetto ha una massa m ed è sottoposto a una forza F. La funzione F è correlato alla forza e alla massa come segue:


Per applicare il metodo di Eulero sono necessari i valori iniziali del tempo t, velocità v e posizione X.
La tabella seguente spiega come a partire dai valori iniziali t1, v1, x1 si possa ottenere un'approssimazione della velocità v2 e della posizione x2, all'istante t2 = t1 + Δt, dove Δt rappresenta un piccolo aumento e corrisponde al passo nel metodo di Eulero.

Esercizio 4
IV) Uno dei problemi fondamentali in meccanica è quello di un blocco di massa M legato ad una molla (o molla) di costante elastica K.
La seconda legge di Newton per questo problema sarebbe simile a questa:
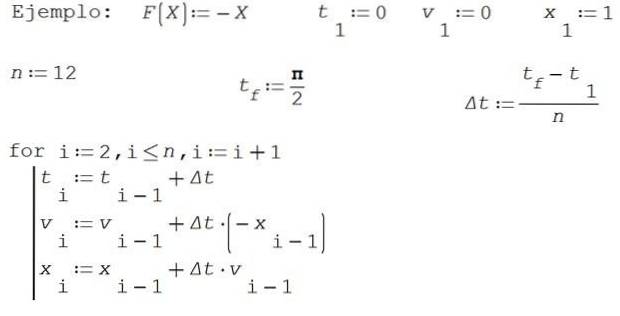
In questo esempio, per semplicità prenderemo M = 1 e K = 1. Trova soluzioni approssimative per la posizione X e velocità v con il metodo di Eulero sull'intervallo di tempo [0, π / 2] suddividendo l'intervallo in 12 parti.
Prendi 0 come istante iniziale, velocità iniziale 0 e posizione iniziale 1.
Soluzione
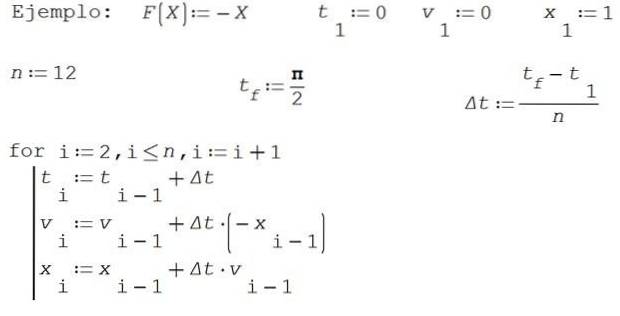
I risultati numerici sono riportati nella tabella seguente:
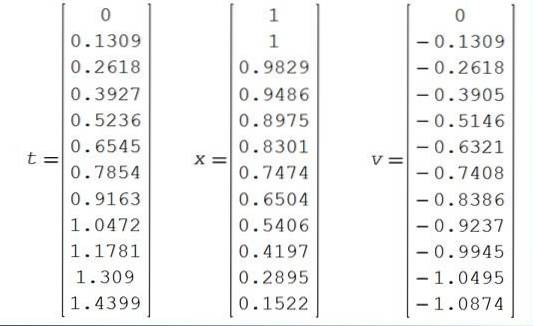
Vengono inoltre visualizzati i grafici della posizione e della velocità tra gli istanti 0 e 1.44..
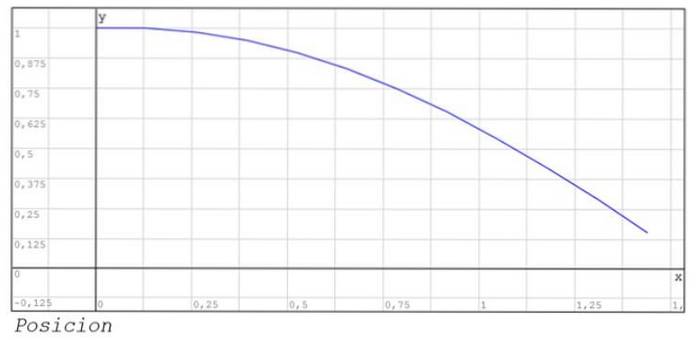
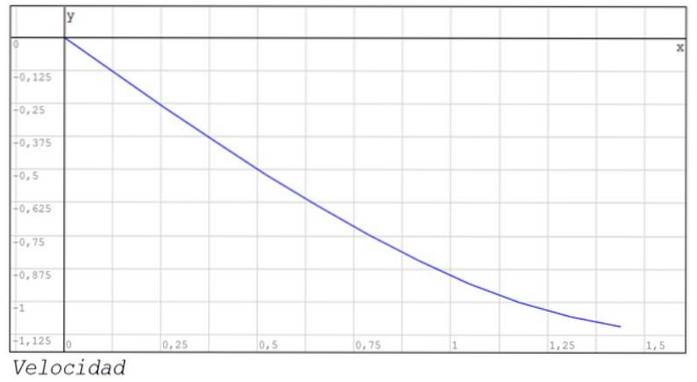
Proposte di esercizi per la casa
Esercizio 1
Usa un foglio di calcolo per determinare una soluzione approssimativa usando il metodo di Eulero per l'equazione differenziale:
y '= - Exp (-y) con le condizioni iniziali x = 0, y = -1 nell'intervallo x = [0, 1]
Inizia con un passaggio di 0,1. Traccia il risultato.
Esercizio 2
Utilizzando un foglio di calcolo trovare soluzioni numeriche alla seguente equazione quadratica, dove y è una funzione della variabile indipendente t.
y "= - 1 / y² con la condizione iniziale t = 0; y (0) = 0,5; y '(0) = 0
Trova la soluzione sull'intervallo [0,5; 1.0] utilizzando un passo di 0,05.
Traccia il risultato: y vs t; y 'vs t
Riferimenti
- Metodo di Eurler Tratto da wikipedia.org
- Risolutore di Eulero. Tratto da en.smath.com
Nessun utente ha ancora commentato questo articolo.