Il moto rotatorio della terra è quello su cui gira il nostro pianeta Asse terrestre in direzione ovest-est e dura circa un giorno, precisamente 23 ore, 56 minuti e 3,5 secondi.
Questo movimento, insieme alla traslazione intorno al sole, sono i più importanti che la Terra abbia. In particolare, il movimento rotatorio è molto influente nella vita quotidiana degli esseri viventi, poiché dà origine a giorni e notti.
Pertanto, ogni intervallo di tempo ha una certa quantità di illuminazione solare, che è ciò che viene comunemente chiamato giorno, e assenza di luce solare o notte. La rotazione della Terra porta anche cambiamenti di temperatura, poiché il giorno è un periodo di riscaldamento, mentre la notte è un periodo di raffreddamento..
Queste circostanze segnano una pietra miliare in tutti gli esseri viventi che popolano il pianeta, dando luogo a una moltitudine di adattamenti in termini di abitudini di vita. Secondo esso, le aziende hanno stabilito i periodi di attività e di riposo secondo i loro costumi e influenzati dall'ambiente..
Ovviamente, le zone chiare e scure cambiano durante il movimento. Quando si divide 360º che ha una circonferenza, tra le 24 ore a cui viene arrotondato un giorno, si scopre che in 1 ora la terra ha ruotato di 15º in direzione ovest-est.
Pertanto, se ci spostiamo a ovest di 15º è un'ora prima, accade il contrario se viaggiamo verso est.
La velocità di rotazione della Terra sul proprio asse è stata stimata in 1600 km / h all'equatore, con la conseguente diminuzione man mano che si avvicina ai poli, fino a annullarsi proprio sull'asse di rotazione..
Indice articolo
Il motivo per cui la Terra ruota attorno al proprio asse risiede nelle origini del sistema solare. Forse il Sole ha trascorso molto tempo solo dopo che la gravità ha reso possibile la sua nascita dalla materia amorfa che popola lo spazio. Quando il Sole si è formato, ha acquisito la rotazione fornita dalla primitiva nuvola di materia..
Parte della materia che ha dato origine alla stella è stata compattata attorno al Sole per creare i pianeti, che avevano anche la loro parte del momento angolare della nuvola originale. In questo modo, tutti i pianeti (compresa la Terra) hanno il proprio movimento di rotazione nella direzione ovest-est, ad eccezione di Venere e Urano, che ruotano nella direzione opposta..
Alcuni credono che Urano si sia scontrato con un altro pianeta di densità simile e, a causa dell'impatto, abbia cambiato asse e direzione di rotazione. Su Venere, l'esistenza di maree gassose potrebbe spiegare perché la direzione di rotazione si sia lentamente invertita nel tempo.
Il momento angolare è, in rotazione, ciò che il momento lineare è per la traslazione. Per un corpo che ruota attorno a un asse fisso come la Terra, la sua grandezza è data da:
L = Iω
In questa equazione L è il momento angolare (kg.mDue/ S), io è il momento d'inerzia (kg.mDue) Y w è la velocità angolare (radianti / s).
Il momento angolare viene conservato fintanto che non c'è coppia netta che agisce sul sistema. Nel caso della formazione del sistema solare, il Sole e la materia che ha dato origine ai pianeti è considerato come un sistema isolato, sul quale nessuna forza ha causato una coppia esterna.
Supponendo che la Terra sia una sfera perfetta e si comporti come un corpo rigido e utilizzando i dati forniti, il suo momento angolare di rotazione deve essere trovato: a) attorno al proprio asse eb) nel suo movimento di traslazione attorno al Sole.
Dati: momento d'inerzia di una sfera = Isfera = (2/5) MRDue; massa terrestre M = 5,9721024 Kg, raggio della Terra R = 6371 Km; distanza media tra la Terra e il Sole Rm = 149,6 x 106 Km.
a) Per prima cosa è necessario considerare il momento di inerzia della Terra come una sfera di raggio R e massa M.
I = (2/5) ' 5.972 1024 Kg '(6371'103 Km)Due = 9,7 '1037 kg.mDue
La velocità angolare viene calcolata in questo modo:
ω = 2π/ T
Dove T è il periodo del movimento, che in questo caso è di 24 ore = 86400 s, quindi:
ω = 2π/ T = 2π/ 86400 s = 0,00007272 s-1
Il momento angolare della rotazione attorno al proprio asse è:
L = 9,7 '1037 kg.mDue' 0.00007272 s-1 = 7,05'1033 kg.mDue/ S
b) Per quanto riguarda il moto di traslazione attorno al Sole, la Terra può essere considerata un oggetto puntuale, il cui momento d'inerzia è I = M.RDuem
I = M.RDuem= 5.972 1024 Kg'(149.6 ' 106 × 1000 m)Due = 1,33'1047kg.mDue
In un anno sono 365 ×24 × 86400 s = 3.1536 × 107 S, la velocità angolare orbitale della Terra è:
ω = 2π/ T = 2π/3.1536 × 107 s = 1,99 ×10-7 S-1
Con questi valori il momento angolare orbitale della Terra è:
L = 1,33'1047kg.mDue × 1 .99 × 10-7 S-1 = 2,65 × 1040 kg.mDue/ S
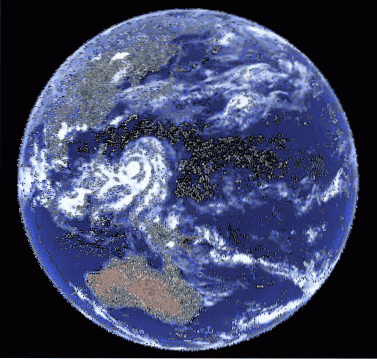
Come accennato in precedenza, il susseguirsi dei giorni e delle notti, con i rispettivi cambiamenti nelle ore di luce e temperatura, sono la conseguenza più importante del movimento rotatorio della Terra sul proprio asse. Tuttavia, la sua influenza si estende un po 'oltre questo fatto decisivo:
- La rotazione della Terra è strettamente correlata alla forma del pianeta. La Terra non è una sfera perfetta come una palla da biliardo. Durante la rotazione si sviluppano forze che lo deformano, provocando rigonfiamenti all'equatore e conseguenti appiattimenti ai poli..
- La deformazione della Terra dà luogo a piccole fluttuazioni nel valore dell'accelerazione di gravità g in posti diversi. Ad esempio, il valore di g è maggiore ai poli che all'equatore.
- Il movimento rotatorio influenza notevolmente la distribuzione delle correnti oceaniche e influenza notevolmente i venti, poiché le masse d'aria e d'acqua subiscono deviazioni dalla loro traiettoria sia in senso orario (emisfero nord) che in senso orario. Direzione opposta (emisfero sud).
- Il Fusi orari, per regolare il passare del tempo in ogni luogo, poiché diverse aree della Terra vengono illuminate dal sole o oscurate.
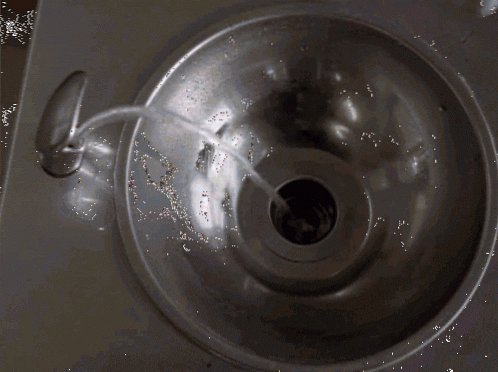
L'effetto Coriolis è una conseguenza della rotazione terrestre. Poiché c'è un'accelerazione in tutte le rotazioni, la Terra non è considerata un sistema di riferimento inerziale, che è ciò che è necessario per applicare le leggi di Newton.
In questo caso compaiono le cosiddette pseudo-forze, forze la cui origine non è fisica, come la forza centrifuga sperimentata dai passeggeri di un'auto quando fa una curva e si sentono deviati da un lato..
Per visualizzarne gli effetti si consideri il seguente esempio: ci sono due persone A e B su una pedana in rotazione antioraria, entrambe ferme rispetto ad essa. La persona A lancia una palla alla persona B, ma quando la palla raggiunge il punto in cui si trovava B, si è già mossa e la palla è deviata di una certa distanza. S, passando dietro B.
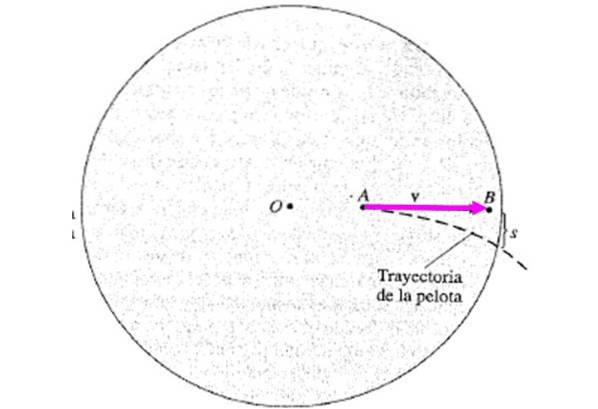
La forza centrifuga non è responsabile in questo caso, agisce già fuori dal centro. Questa è la forza di Coriolis, il cui effetto è deviare lateralmente la palla. Succede che sia A che B hanno velocità di salita diverse, perché si trovano a distanze diverse dall'asse di rotazione. La velocità di B è maggiore e sono dati da:
vPER = ωRPER ; vB = ωRB
L'accelerazione di Coriolis ha effetti significativi sul movimento delle masse d'aria, e quindi influisce sul clima. Ecco perché è importante tenerne conto per studiare come si muovono le correnti d'aria e le correnti oceaniche..
Le persone possono sperimentarlo anche quando provano a camminare su una piattaforma rotante, come una giostra in movimento..
Per il caso mostrato nella figura precedente, si supponga di non tenere conto della gravità e di visualizzare il movimento da un sistema di riferimento inerziale, esterno alla piattaforma. In questo caso, la mossa ha questo aspetto:
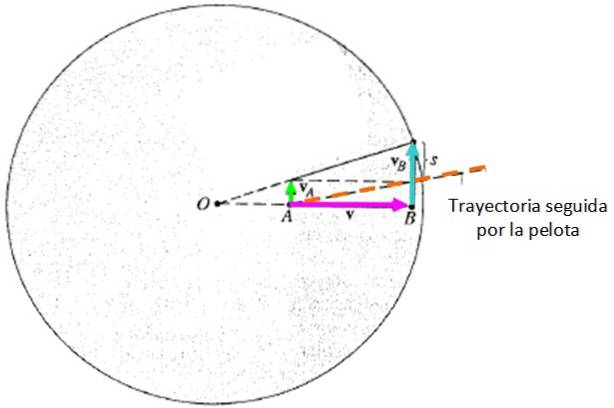
La deviazione subita dalla palla dalla posizione originale della persona B è:
s = sB - SPER = vt = (vB - vPER) t = (ωRB - ωRPER) t = = ω(RB - RPER) t
Ma RB - RPER = vt, quindi:
s = ω .(vt). t = ωvtDue
È un movimento con velocità iniziale 0 e accelerazione costante:
s = ½ aCoriolis tDue
perCoriolis = 2ω.v
Nessun utente ha ancora commentato questo articolo.