
Quantità di momento angolare, conservazione, esempi, esercizi
Il momento angolare o il momento angolare è, per il movimento rotatorio, ciò che il momento lineare è per il movimento traslatorio. È una quantità vettoriale che caratterizza la rotazione di una particella puntiforme o di un oggetto esteso attorno a un asse che passa per un punto.
Ciò significa che ogni volta che si deve calcolare il momento angolare, l'asse di rotazione deve essere specificato in modo appropriato.
Partendo da un punto materiale di massa m, il momento angolare è indicato con L, momento lineare come p e la posizione della particella rispetto ad un asse che passa per un certo punto O è r, poi:
L = r X p
Le lettere in grassetto sono riservate alle quantità vettoriali e la croce significa che il momento angolare è il prodotto vettoriale tra il vettore di posizione r e il momento lineare p della particella. Il vettore che risulta da un prodotto vettoriale è perpendicolare al piano formato dai vettori partecipanti.
Ciò significa che la direzione e il senso di L può essere trovato usando la regola della mano destra per il prodotto incrociato.
Nel Sistema internazionale di unità SI, le unità del momento angolare sono kg⋅mDue/ i, che non hanno un nome speciale. E per un corpo esteso, che è composto da molte particelle, la definizione di cui sopra è convenientemente estesa.
Indice articolo
- 1 Quantità di movimento angolare
- 1.1 Il momento d'inerzia
- 2 Momento angolare di un sistema di particelle
- 3 Quando varia il momento angolare?
- 4 Conservazione del momento angolare
- 5 esempi
- 5.1 Pattinaggio di figura e altri sport
- 5.2 I gatti atterrano in piedi
- 5.3 Il movimento di un frisbee
- 5.4 Palloni nello sport
- 5.5 La distanza dalla luna
- 5.6 L'atomo
- 6 Esercizio risolto
- 6.1 Soluzione
- 7 Riferimenti
Quantità di movimento angolare
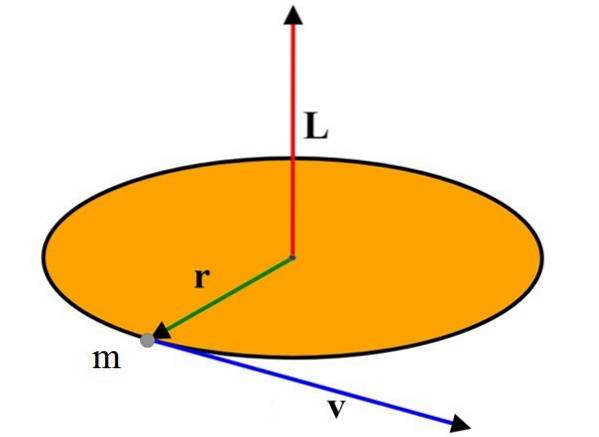
L'entità del vettore del momento angolare è secondo la definizione del prodotto vettoriale:
L = r⋅m⋅v⋅sen ϕ = mv (r⋅sen ϕ) = mvℓ
Dove ϕ è l'angolo tra i vettori r Y v. Allora ℓ = r sin ϕ è la distanza perpendicolare tra la linea di v e il punto O.
Per il caso della particella che si muove descrivendo la circonferenza mostrata nell'immagine in alto, questo angolo è di 90º, poiché la velocità è sempre tangente alla circonferenza e quindi perpendicolare al raggio..
Quindi sin 90º = 1 e la grandezza di L è:
L = m⋅r⋅v
Momento d'inerzia
Il momento di inerzia di un corpo rigido descrive l'inerzia del corpo contro la rotazione attorno a un certo asse.
Dipende non solo dalla massa del corpo, ma anche dalla distanza dall'asse di rotazione. Ciò è facilmente comprensibile quando si pensa che per alcuni oggetti è più facile ruotare attorno ad alcuni assi rispetto ad altri..
Per un sistema di particelle, il momento di inerzia, indicato dalla lettera I, è dato da:
I = ∑ rioDue Δmio
Dove Δmio è una piccola porzione di pasta e rio è la sua distanza dall'asse di rotazione. Un corpo esteso è composto da numerose particelle, quindi il suo momento d'inerzia totale è la somma di tutti i prodotti tra la massa e la distanza, delle particelle che lo compongono..
Se si tratta di un corpo esteso, la somma cambia in un integrale e Δm diventa un differenziale di massa dm. I limiti di integrazione dipendono dalla geometria dell'oggetto:
I = ∫M (rDue) dm
Il concetto di momento d'inerzia è strettamente correlato al momento angolare di un oggetto esteso, come vedremo di seguito.
Momento angolare di un sistema di particelle
Considera un sistema di particelle, composto da masse Δmio che ruota seguendo una circonferenza nel piano xy, ognuno ha una velocità lineare correlata alla sua velocità angolare, quest'ultima uguale per tutte le particelle:
vio = ωrio
Dove rio è la distanza dall'asse di rotazione O. Quindi l'entità del momento angolare è:
Lio = Δmio. rio. (ωrio) = rioDueω Δmio
Il momento angolare del sistema sarà dato dalla somma:
L = ω ∑ rioDue Δmio
Identifichiamo rapidamente il momento di inerzia, come definito nella sezione precedente, e quindi l'entità del suo momento angolare è la seguente:
L = Iω
Come abbiamo detto che il sistema particellare era nel piano xy, risulta che il momento angolare è diretto lungo l'asse z, perpendicolare a detto piano. La direzione è data da quella della rotazione: il momento angolare è positivo se la rotazione viene eseguita in senso antiorario.
Un corpo esteso può essere diviso in fette, ciascuna con momento angolare dato da L = Iω diretto lungo l'asse z. Se l'asse di simmetria dell'oggetto coincide con l'asse z, non c'è problema, poiché anche per punti che non sono nel piano xy, le componenti del momento angolare perpendicolari a quell'asse si annullano.
Vettorialmente:
L = Iω
Questa equazione è valida per oggetti tridimensionali che ruotano attorno a un asse di simmetria.
Quando varia il momento angolare?
Quando una forza netta agisce su una particella o un corpo, la sua quantità di moto può cambiare e, di conseguenza, anche il suo momento angolare. Per sapere quando varia, utilizziamo il derivato, che ci darà il tasso di variazione nel tempo, se ce n'è uno:

Applicazione della regola del prodotto per il derivato:

Il termine v x mv è nullo, poiché è il prodotto di un vettore con se stesso, e nel secondo termine troviamo la forza netta F = mper, Quindi:

Il prodotto vettoriale r X F non è altro che la coppia o coppia netta, a volte denotata dalla lettera greca τ o come M, sempre in grassetto, poiché è una quantità vettoriale. Quindi, in analogia con il momento lineare, il momento angolare varia fintanto che esiste una coppia o coppia netta:
dL/ dt = M
Conservazione del momento angolare
Dalle sezioni precedenti abbiamo visto che:
dL/ dt = M
Cioè, il momento angolare varia quando c'è una coppia netta. Se non è presente una coppia netta, allora:
dL/ dt = 0 → L è costante
In altre parole:
Momento angolare iniziale = Momento angolare finale
Questo risultato è comunque valido anche nel caso in cui un corpo non sia rigido, come vedremo negli esempi seguenti.
Esempi
Il momento angolare è una grandezza importante che si rivela in molte situazioni, il che mostra quanto sia universale:
Pattinaggio artistico e altri sport

Ogni volta che un corpo rotante si contrae, la sua velocità di rotazione aumenta, questo è ben noto ai pattinatori sul ghiaccio..
Ciò è dovuto al fatto che quando braccia e gambe si contraggono, il momento di inerzia I diminuisce, poiché la distanza tra le loro parti diminuisce, ma poiché il momento angolare è conservato, per mantenere costante il prodotto Iω, la velocità angolare deve aumentare.
Ciò è valido non solo nel pattinaggio, ma anche negli sport e nelle attività in cui è necessario fare turni, come i subacquei e i trapezisti nel circo..
I gatti atterrano in piedi

I gatti riescono sempre ad atterrare a quattro zampe quando cadono. Sebbene non abbiano uno slancio iniziale, si assicurano di girare rapidamente le gambe e la coda per cambiare la loro inerzia rotazionale e riescono ad atterrare in piedi..
Allo stesso modo, mentre manovrano, il loro momento angolare è zero, poiché la loro rotazione non è continua..
Il movimento di un frisbee

Un frisbee deve essere lanciato dandogli un giro in modo che voli, altrimenti cadrà. In effetti, il momento angolare fornito dal lanciatore conferisce al disco una stabilità sufficiente per muoversi ulteriormente nell'aria..
Palle nello sport

Le palle nel baseball, nel calcio, nel basket e in altri sport hanno un momento angolare. Essendo sferiche, hanno momento di inerzia e vengono ruotate durante il gioco. Poiché il momento di inerzia di una sfera è:
I = (2/5) MRDue
Dove M è la massa della palla e R il suo raggio, il momento di inerzia attorno a un certo asse (fisso) è:
L = (2/5) MRDueω
La partenza dalla luna
La Luna si sta allontanando dalla Terra, poiché la velocità di rotazione della Terra diminuisce a causa dell'attrito tra grandi masse d'acqua e il fondo del mare.
Il sistema Terra-Luna conserva il suo momento angolare, quindi, se la Terra diminuisce il suo contributo, la Luna aumenta il suo contributo allontanandosi dalla Terra..
L'atomo
Il primo postulato del modello atomico di Bohr afferma che un elettrone occupa solo orbite in cui il momento angolare è un multiplo intero di h / 2π, dove h è la costante di Planck.
Esercizio risolto
Una sottile barra d'acciaio ha una massa di 500 ge una lunghezza di 30 cm. Ruota attorno a un asse passante per il suo centro a una velocità di 300 giri al minuto. Determina il modulo del suo momento angolare.
Soluzione
Avremo bisogno del momento d'inerzia dell'asta riferito ad un asse che passa per il suo centro. Consultando le tabelle dei momenti d'inerzia si riscontra che:
I = (1/12) MLDue = (1/12) × 0,5 kg x (30 × 10-Due m)Due = 3,75 × 10-3 kg.mDue
Trattandosi di un corpo allungato, di cui conosciamo la velocità angolare, utilizziamo:
L = Iω
Prima di trasformare la velocità angolare o la frequenza angolare ω in radianti / s:
ω = (300 giri / minuto) × (1 minuto / 60 secondi) x (2π radianti / giro) = 10 π rad / s
Sostituzione:
L = 3,75 x10-3 kg⋅mDue × 10 π rad / s = 0,118 kg⋅mDue / S
Riferimenti
- Bauer, W. 2011. Fisica per l'ingegneria e le scienze. Volume 1. Mc Graw Hill.
- Giambattista, A. 2010. Fisica. 2 °. Ed. McGraw Hill.
- Giancoli, D. 2006. Fisica: principi con applicazioni. 6 °. Ed prentice hall.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Serway, R., Jewett, J. (2008). Fisica per la scienza e l'ingegneria. Volume 1. 7th. Ed. Cengage Learning.
- .



Nessun utente ha ancora commentato questo articolo.