Elementi di algebra a blocchi, esempi, esercizi risolti

Il algebra a blocchi si riferisce all'insieme di operazioni eseguite tramite blocchi. Questi e alcuni altri elementi servono a rappresentare schematicamente un sistema e visualizzare facilmente la sua risposta a un dato input..

In generale, un sistema contiene vari elementi elettrici, elettronici ed elettromeccanici, e ciascuno di essi, con la rispettiva funzione e posizione nel sistema, nonché il modo in cui sono correlati, è delineato tramite blocchi funzionali.

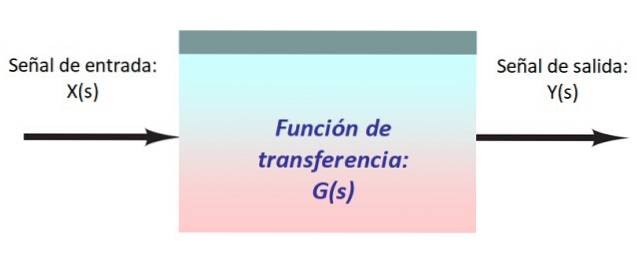
Nella figura sopra è presente un sistema molto semplice, costituito da un segnale di ingresso X (s), che entra nel blocco con la funzione di trasferimento G (s) che lo modifica e produce l'uscita Y (s).

Conviene rappresentare i segnali e il loro percorso nel sistema mediante frecce che entrano ed escono da ogni blocco. Di solito il flusso del segnale è diretto da sinistra a destra.

Il vantaggio di questo tipo di schema è l'aiuto visivo che fornisce nella comprensione del sistema, anche se non è una rappresentazione fisica del sistema. Lo schema a blocchi, infatti, non è univoco, perché a seconda del punto di vista si possono disegnare anche più schemi dello stesso sistema..

Può anche accadere che lo stesso diagramma serva più sistemi non necessariamente correlati tra loro, purché ne descriva adeguatamente il comportamento. Esistono diversi sistemi la cui risposta è simile sotto molti aspetti, ad esempio un circuito LC (induttore-condensatore) e un sistema massa-molla..

Indice articolo

• 1 Cos'è uno schema a blocchi?
• 2 Elementi dello schema a blocchi
  • 2.1 Il segnale
  • 2.2 Il blocco
  • 2.3 Punto di somma
  • 2.4 Punto di diramazione
• 3 Esempi di regole di algebra a blocchi
  • 3.1 Blocchi in cascata
  • 3.2 Blocchi in parallelo
  • 3.3 Spostare un sommatore a sinistra
  • 3.4 Spostare un sommatore a destra
  • 3.5 Spostamento di un punto di diramazione da sinistra a destra
  • 3.6 Spostare un punto di diramazione da destra a sinistra
  • 3.7 Sistema di feedback
  • 3.8 Sistema con feedback e trasduttore
• 4 Esercizi risolti
  • 4.1 Esercizio 1
  • 4.2 Esercizio 2
• 5 Riferimenti

Cos'è un diagramma a blocchi?

I sistemi sono generalmente più complicati di quello della Figura 1, ma l'algebra a blocchi fornisce una serie di semplici regole per manipolare lo schema del sistema e ridurlo alla sua versione più semplice..

Come spiegato all'inizio, il diagramma utilizza blocchi, frecce e cerchi per stabilire la relazione tra ogni componente del sistema e il flusso di segnali che lo attraversa..

L'algebra a blocchi consente di confrontare due o più segnali sommandoli, sottraendoli e moltiplicandoli, oltre ad analizzare il contributo che ogni componente dà al sistema.

Grazie a ciò è possibile ridurre l'intero sistema ad un unico segnale di ingresso, un'unica funzione di trasferimento che descrive in modo completo l'azione del sistema e la corrispondente uscita..

Elementi dello schema a blocchi

Gli elementi dello schema a blocchi sono i seguenti:

Il segnale

I segnali sono di natura molto varia, ad esempio è comune che sia una corrente elettrica o un voltaggio, ma può essere leggero, sonoro e altro. L'importante è che contenga informazioni su un determinato sistema.

Il segnale è indicato con una lettera maiuscola se è una funzione della variabile S della trasformata di Laplace: X (s) (vedi figura 1) o minuscolo se funzione del tempo t, come x (t).

Nello schema a blocchi, il segnale in ingresso è rappresentato da una freccia diretta verso il blocco, mentre il segnale in uscita, indicato come Y (s) o y (t), è indicato da una freccia in uscita.

Entrambi i segnali di ingresso e di uscita sono unici e la direzione del flusso di informazioni è determinata dalla direzione della freccia. E l'algebra è la stessa per una delle due variabili.

Il blocco

Il blocco è rappresentato da un quadrato o da un rettangolo (vedi figura 1) e può essere utilizzato per eseguire operazioni o implementare la funzione di trasferimento, solitamente indicata con la lettera maiuscola G. Questa funzione è un modello matematico che descrive la risposta offerto dal sistema a un segnale in ingresso.

La funzione di trasferimento può essere espressa in termini di tempo t come G (t) o la variabile S come G (s).

Quando il segnale di ingresso X (s) raggiunge il blocco, viene moltiplicato per la funzione di trasferimento e trasformato nel segnale di uscita Y (s). Matematicamente si esprime così:

Y (s) = X (s) .G (s)

Equivalentemente, la funzione di trasferimento è il rapporto tra la trasformata di Laplace del segnale di uscita e la trasformata di Laplace del segnale di ingresso, a condizione che le condizioni iniziali del sistema siano nulle:

G (s) = Y (s) / X (s)

Punto di somma

Il punto di addizione, o sommatore, è simboleggiato da un cerchio con una croce all'interno. Serve per combinare, mediante addizione e sottrazione, due o più segnali. Alla fine della freccia che simboleggia il segno, viene posto direttamente un segno + se si aggiunge detto segno o un segno - se viene sottratto..

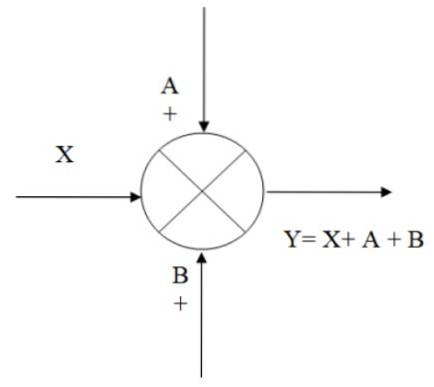
Nella figura seguente è riportato un esempio di come funziona il sommatore: abbiamo il segnale di ingresso X, a cui si sommano i segnali A e B, ottenendo come risultato l'uscita Y, che è algebricamente equivalente a:

Y = X + A + B

Punto di diramazione

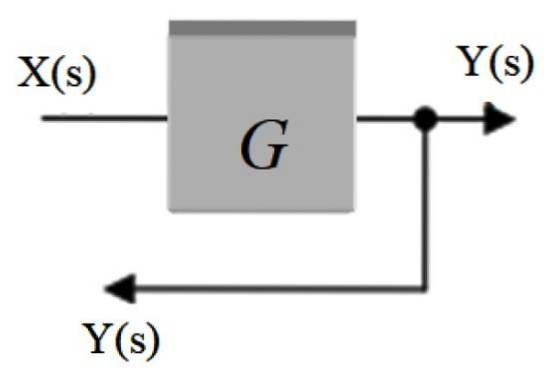
Si chiama anche punto di biforcazione. In esso, il segnale che esce da un blocco viene distribuito ad altri blocchi o ad un sommatore. È rappresentato da un punto posto sulla freccia del segnale e ne esce un'altra freccia che reindirizza il segnale ad un'altra parte.

Esempi di regole di algebra a blocchi

Come spiegato prima, l'idea è di esprimere il sistema utilizzando lo schema a blocchi e ridurlo per trovare la funzione di trasferimento che lo descrive. Le seguenti sono le regole di algebra a blocchi per semplificare i diagrammi:

Blocchi a cascata

Quando hai un segnale che passa successivamente attraverso i blocchi G.₁, G_Due, G₃..., si riduce ad un unico blocco la cui funzione di trasferimento è il prodotto di G₁, G_Due, G₃...

Nell'esempio seguente, il segnale X (s) entra nel primo blocco e la sua uscita è:

Y₁(s) = X (s) .G₁(S)

Gira Y₁(s) entrare nel blocco G_Due(s), il cui output è:

Y_Due(s) = X (s) .G₁(S). G_Due(S)

La procedura è valida per n blocchi in cascata:

Y_n (s) = X (s). G₁(s) .G_Due(i) ... G_n(S)

Blocchi paralleli

Nel diagramma a sinistra, il segnale X (s) si dirama per entrare nei blocchi G.₁(s) e G_Due(S):

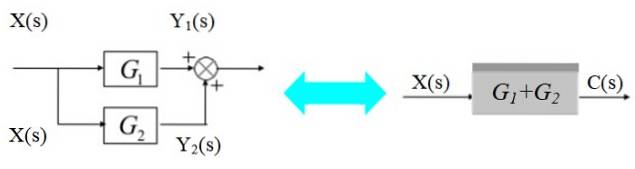
I rispettivi segnali di uscita sono:

Y₁(s) = X (s) .G₁(S)

Y_Due(s) = X (s) .G_Due(S)

Questi segnali vengono sommati per ottenere:

C (s) = Y₁(s) + Y_Due(s) = X (s). [G₁(s) + G_Due(S)]

Come mostrato nel diagramma a destra.

Sposta un sommatore a sinistra

Un sommatore può essere spostato a sinistra del blocco come segue:

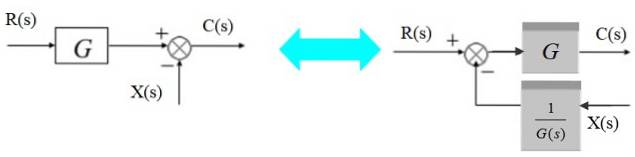
A sinistra il segnale di uscita è:

C (s) = R (s). G (s) - X (s)

Equivalentemente a destra:

C (s) = [R (s) - X (s) / G (s)]. G (s)

Sposta una vipera a destra

Il sommatore può essere spostato a destra del blocco in questo modo:

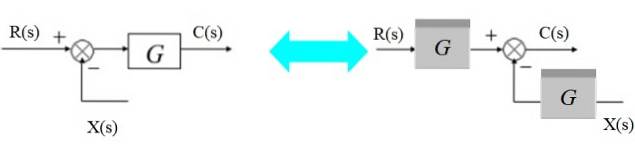
A sinistra abbiamo: [R (s) - X (s)]. G (s) = C (s)

E a destra:

R (s). G (s) - X (s). G (s) = C (s)

Spostare un punto di diramazione da sinistra a destra

Per spostare il punto di diramazione da sinistra a destra del blocco, basta osservare che l'uscita C (s) a destra è il prodotto X (s) .G (s). Dato che vuoi convertirlo di nuovo in X (s), moltiplica per l'inverso di G (s).

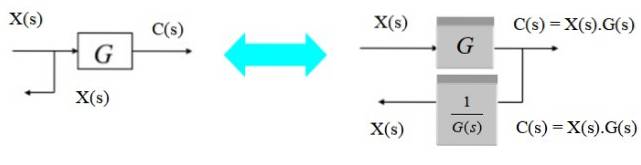
Spostare un punto di diramazione da destra a sinistra

In alternativa, il punto di diramazione può essere spostato da destra a sinistra come segue:

Poiché all'uscita del ramo vogliamo ottenere C (s), è sufficiente inserire un nuovo blocco G (s) in un punto di diramazione a sinistra del blocco originale.

Sistema di feedback

Nel seguente sistema il segnale di uscita C (s) viene ritrasmesso attraverso il sommatore a sinistra:

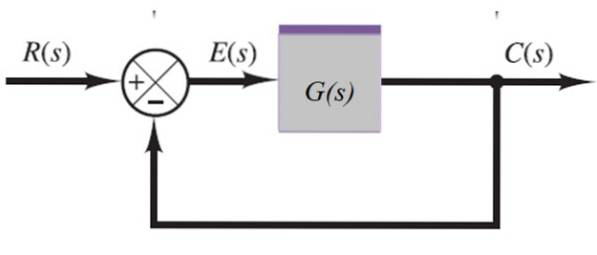
C (s) = E (s). G (s)

Ma:

E (s) = R (s) -C (s)

Sostituendo questa espressione nell'equazione precedente rimane: C (s) = [R (s) -C (s)]. G (s), da cui C (s) può essere risolto:

C (s) + C (s). G (s) = R (s) .G (s) → C (s). [1 + G (s)] = R (s) .G (s)

C (s) = R (s). G (s) / [1 + G (s)]

O in alternativa:

C (s) / R (s) = G (s) / [1 + G (s)]

In forma grafica, dopo aver semplificato rimane:

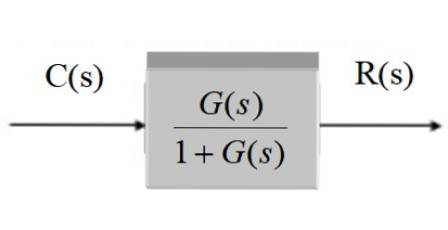
Sistema con feedback e trasduttore

Il trasduttore è costituito dalla funzione di trasferimento H (s):

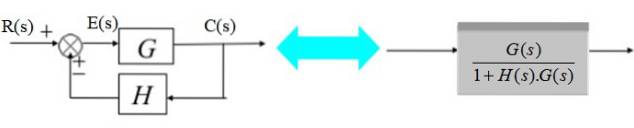
Nel diagramma a destra, il segnale di uscita C (s) è:

C (s) = E (s). G (s) con E (s) = R (s) - C (s). H (s)

Poi:

C (s) = [R (s) - C (s). H (s)]. G (s)

C (s) [1+ H (s) .G (s)] = R (s) .G (s)

Pertanto, C (s) può essere risolto da:

C (s) = G (s) .R (s) / [1+ H (s) .G (s)]

E la funzione di trasferimento sarà:

G (s) / [1+ H (s) .G (s)]

Come mostrato nel diagramma semplificato a destra.

Esercizi risolti

Esercizio 1

Trova la funzione di trasferimento del seguente sistema:

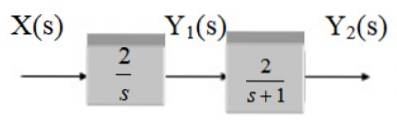
Soluzione

Tratta due blocchi in cascata, quindi la funzione di trasferimento è il prodotto delle funzioni G₁ e G_Due.

Deve:

G₁ = 2 / s

G_Due = 2 / (s + 1)

Pertanto la funzione di trasferimento ricercata è:

G (s) = 4 / [s (s + 1)]

Esercizio 2

Riduci il seguente sistema:

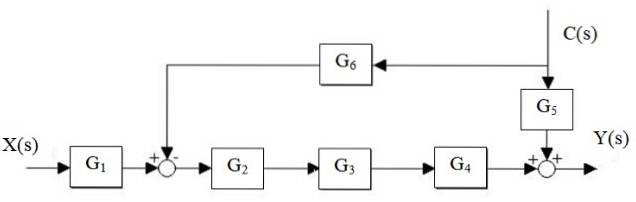
Soluzione

Per prima cosa la cascata G viene ridotta_Due, G₃ e G_4, e il parallelo G è separato₅ e G₆:

Quindi il sommatore a sinistra del blocco G_Due ⋅G₃ ⋅ G₄ si sposta a destra:

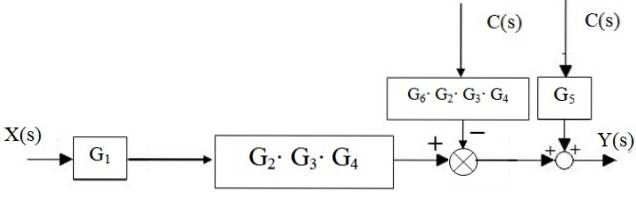
I sommatori a destra sono ridotti a uno solo, così come i blocchi a cascata:

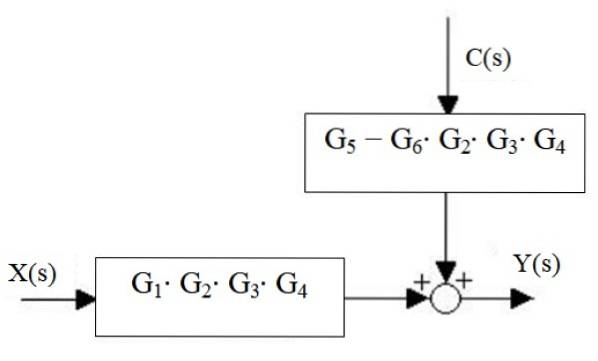
Infine, l'output del sistema è:

Y (s) = X (s) ⋅G₁⋅ G_Due ⋅G₃ ⋅ G₄ + C (s) ⋅ [G₅ - G₆ ⋅ G_Due ⋅G₃ ⋅ G₄]

Riferimenti

1. Alaydi, J. Schema a blocchi del sistema di controllo. Estratto da: site.iugaza.edu.ps.
2. Bolton, W. 2006. Ingegneria di controllo. 2 °. Edizione. Alfa Omega.
3. Cwalinsky, J. Introduzione all'algebra a blocchi di sistema. Estratto da: cedengineering.com.
4. Dademuchconnection. Schema a blocchi. Estratto da: dademuch.com.
5. Ogata, K. 2010. Moderna ingegneria di controllo. 5 °. Edizione. Pearson.