Leggi degli esponenti (con esempi ed esercizi risolti)

Il leggi degli esponenti sono quelli che si applicano a quel numero che indica quante volte un numero base deve essere moltiplicato per se stesso. Gli esponenti sono anche conosciuti come potenze. L'empowerment è un'operazione matematica formata da una base (a), l'esponente (m) e la potenza (b), che è il risultato dell'operazione.

Gli esponenti sono generalmente usati quando si usano quantità molto grandi, perché queste non sono altro che abbreviazioni che rappresentano la moltiplicazione di uno stesso numero un certo numero di volte. Gli esponenti possono essere sia positivi che negativi.

Indice articolo

• 1 Spiegazione delle leggi degli esponenti
  • 1.1 Prima legge: potenza dell'esponente pari a 1
  • 1.2 Seconda legge: potenza dell'esponente pari a 0
  • 1.3 Terza legge: esponente negativo
  • 1.4 Quarta legge: moltiplicazione dei poteri con base uguale
  • 1.5 Quinta legge: divisione dei poteri su base uguale
  • 1.6 Sesta legge: moltiplicazione dei poteri con base diversa
  • 1.7 Settima legge: divisione dei poteri con base diversa
  • 1.8 Ottava legge: potere di un potere
  • 1.9 Nona legge: esponente frazionario
• 2 Esercizi risolti
  • 2.1 Esercizio 1
  • 2.2 Esercizio 2
• 3 Riferimenti

Spiegazione delle leggi degli esponenti

Come affermato sopra, gli esponenti sono una forma abbreviata che rappresenta la moltiplicazione dei numeri per se stessi più volte, dove l'esponente si riferisce solo al numero a sinistra. Per esempio:

Due³ = 2 * 2 * 2 = 8

In quel caso il numero 2 è la base della potenza, che verrà moltiplicata 3 volte come indicato dall'esponente, posto nell'angolo in alto a destra della base. Esistono diversi modi per leggere l'espressione: 2 elevato a 3 o anche 2 elevato a cubo.

Gli esponenti indicano anche il numero di volte che possono essere divisi, e per differenziare questa operazione dalla moltiplicazione l'esponente ha davanti il ​​segno meno (-) (è negativo), il che significa che l'esponente è al denominatore di a frazione. Per esempio:

Due^{- 4} = 1/2 * 2 * 2 * 2 = 1/16

Questo non deve essere confuso con il caso in cui la base è negativa, poiché dipenderà dal fatto che l'esponente sia dispari o pari per determinare se la potenza sarà positiva o negativa. Quindi devi:

- Se l'esponente è pari, la potenza sarà positiva. Per esempio:

(-7)^Due = -7 _* -7 = 49.

- Se l'esponente è dispari, la potenza sarà negativa. Per esempio:

(-Due)⁵ = (-2) * (- 2) * (- 2) * (- 2) * (- 2) = - 32.

C'è un caso particolare in cui se l'esponente è uguale a 0, la potenza è uguale a 1. C'è anche la possibilità che la base sia 0; in tal caso, a seconda dell'esponente, la potenza sarà indeterminata o meno.

Per eseguire operazioni matematiche con esponenti è necessario seguire diverse regole o norme che facilitino la ricerca della soluzione di queste operazioni.

Prima legge: potenza dell'esponente pari a 1

Quando l'esponente è 1, il risultato sarà lo stesso valore della base: a¹ = a.

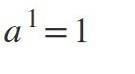
Esempi

9¹ = 9.

22¹ = 22.

895¹ = 895.

Seconda legge: potenza esponente pari a 0

Quando l'esponente è 0, se la base è diversa da zero, il risultato sarà: a⁰ = 1.

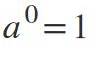
Esempi

1⁰ = 1.

323⁰= 1.

1095⁰ = 1.

Terza legge: esponente negativo

Poiché l'esponte è negativo, il risultato sarà una frazione, dove la potenza sarà il denominatore. Ad esempio, se m è positivo, a^-m = 1 / a^m.

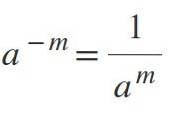
Esempi

- 3^-1 = 1/3.

- 6^-Due = 1/6^Due = 1/36.

- 8^-3 = 1/8³ = 1/512.

Quarta legge: moltiplicazione dei poteri con base uguale

Per moltiplicare le potenze dove le basi sono uguali e diverse da 0, rimane la base e si aggiungono gli esponenti: a^m _* perⁿ = a^{m + n}.    

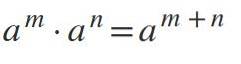
Esempi

- 4⁴ _* 4³ = 4^{4 + 3} = 4⁷

- 8¹ _* 8⁴ = 8^{1 + 4} = 8⁵

- Due^Due _* Due⁹ = 2^{2 + 9} = 2^undici

Quinta legge: divisione dei poteri su base uguale

Per dividere le potenze in cui le basi sono uguali e diverse da 0, la base viene mantenuta e gli esponenti vengono sottratti come segue: a^m / perⁿ = a^m-n.    

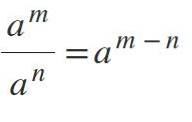
Esempi

- 9^Due / 9¹ = 9 ^(ventuno) = 9¹.

- 6^quindici / 6¹⁰ = 6 ^{(15 - 10)} = 6⁵.

- 49¹² / 49⁶ = 49 ^{(12 - 6)} = 49⁶.

Sesta legge: moltiplicazione dei poteri con base diversa

In questa legge c'è l'opposto di ciò che è espresso nella quarta; cioè se si hanno basi diverse ma con gli stessi esponenti, le basi vengono moltiplicate e l'esponente viene mantenuto: a^m _* b^m = (a_*b) ^m.

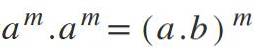
Esempi

- 10^Due _* venti^Due = (10 _* venti)^Due = 200^Due.

- Quattro cinque^undici _* 9^undici = (45 * 9)^{11 =} 405^undici.

Un altro modo per rappresentare questa legge è quando una moltiplicazione viene elevata a potenza. Pertanto, l'esponente apparterrà a ciascuno dei termini: (a_*b)^m= a^m_* b^m.

Esempi

- (5_*8)⁴ = 5⁴ _* 8⁴ = 40⁴.

- (23 * 7)⁶ = 23⁶ _* 7⁶ = 161⁶.

Settima legge: divisione dei poteri con base diversa

Se hai basi diverse ma con gli stessi esponenti, dividi le basi e mantieni l'esponente: a^m / b^m = (a / b)^m.

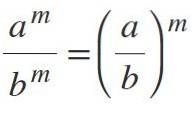
Esempi

- 30³ / Due³ = (30/2)³ = 15³.

- 440⁴ / 80⁴ = (440/80)⁴ = 5,5⁴.

Allo stesso modo, quando una divisione viene elevata a una potenza, l'esponente apparterrà a ciascuno dei termini: (a / b) ^m = a^m / b^m.

Esempi

- (8/4)⁸ = 8⁸ / 4⁸ = 2⁸.

- (25/5)^Due = 25^Due / 5^Due = 5^Due.

C'è il caso in cui l'esponente è negativo. Quindi, per essere positivo, il valore del numeratore viene invertito con quello del denominatore, come segue:

- (a / b)^-n = (b / a)ⁿ = bⁿ / perⁿ.

- (4/5) ^-9 = (5/4) ⁹ = 5⁹ / 4⁴.

Ottava legge: potere di un potere

Quando si ha una potenza che viene elevata ad un'altra potenza, cioè due esponenti contemporaneamente, la base viene mantenuta e gli esponenti vengono moltiplicati: (a^m)ⁿ= a^{m *n}.

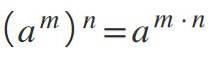
Esempi

- (8³)^Due = 8 ^{(3 * 2)} = 8⁶.

- (13⁹)³ = 13 ^{(9 * 3)} = 13²⁷.

- (238¹⁰)¹² = 238^{(10 * 12)} = 238¹²⁰.

Nona legge: esponente frazionario

Se la potenza ha una frazione come esponente, questo si risolve trasformandola in un'ennesima radice, dove il numeratore rimane come esponente e il denominatore rappresenta l'indice della radice:

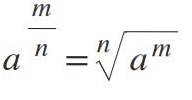
Esempio

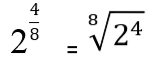
Esercizi risolti

Esercizio 1

Calcola le operazioni tra le potenze che hanno basi diverse:

Due⁴ _* 4⁴ / 8^Due.

Soluzione

Applicando le regole degli esponenti, le basi vengono moltiplicate al numeratore e l'esponente viene mantenuto, in questo modo:

Due⁴ _* 4⁴ / 8^Due= (2_*4)⁴ / 8^Due  = 8⁴ / 8^Due

Ora, poiché abbiamo le stesse basi ma con esponenti diversi, la base viene mantenuta e gli esponenti vengono sottratti:

 8⁴ / 8^Due = 8^{(4 - 2)} = 8^Due

Esercizio 2

Calcola le operazioni tra le potenze elevate ad un'altra potenza:

(3^Due)³ _* (Due _* 6⁵)^-Due _* (Due^Due)³

Soluzione

Applicando le leggi, devi:

(3^Due)³ _* (Due _* 6⁵)^-Due _* (Due^Due)³

= 3⁶ _* Due^-Due _* Due^-10 _* Due⁶

= 3⁶ _* Due^{(-2) + (- 10)} _* Due⁶

= 3⁶ _*  Due^-12 _* Due⁶

= 3⁶ _* Due^{(-12) + (6)}

= 3⁶ _* Due⁶

= (3_*Due)⁶

= 6⁶

= 46.656

Riferimenti

1. Aponte, G. (1998). Fondamenti di matematica di base. Pearson Education.
2. Corbalán, F. (1997). Matematica applicata alla vita quotidiana.
3. Jiménez, J. R. (2009). Matematica 1 SEP.
4. Max Peters, W. L. (1972). Algebra e trigonometria.
5. Rees, P. K. (1986). Reverte.