
Spiegazione delle leggi di Gossen con esempi
Il Le leggi di Gossen, Creati dall'economista tedesco Hermann Gossen (1810-1858), sono tre leggi economiche rilevanti legate alla diminuzione dell'utilità marginale, del costo di acquisizione marginale e della scarsità..
Gossen fu il primo a spiegare la legge dell'utilità marginale decrescente, o la prima legge di Gossen, basata su osservazioni generali del comportamento umano. Questa legge afferma che la quantità dello stesso godimento diminuisce continuamente man mano che si avanza senza interruzione in quel godimento, finché non si ottiene la soddisfazione..

La seconda legge, la legge dell'utilità equi-marginale, spiega il comportamento dei consumatori quando hanno risorse limitate, ma desideri illimitati..
Il problema fondamentale in un'economia è che i desideri umani sono illimitati, ma non ci sono risorse adeguate per soddisfare tutti i desideri umani. Pertanto, un individuo razionale cerca di ottimizzare le scarse risorse disponibili per ottenere la massima soddisfazione..
La terza legge si riferisce al valore economico dei prodotti, che risulta da una precedente carenza.
Gossen si sforzò di trovare ciascuna di queste leggi in tutti i tipi di attività economiche.
Indice articolo
- 1 Prima legge di Gossen
- 1.1 Esempio
- 2 Seconda legge di Gossen
- 2.1 Esempio
- 3 Terza legge di Gossen
- 4 Riferimenti
Prima legge di Gossen
È conosciuta come la legge dell'utilità marginale decrescente. Afferma che quando un individuo consuma più di un prodotto, l'utilità totale aumenta a un ritmo decrescente.
Tuttavia, dopo una certa fase, anche l'utilità totale inizia a diminuire e l'utilità marginale diventa negativa. Ciò significa che l'individuo non ha più bisogno del prodotto..
Cioè, il desiderio di un individuo per un particolare prodotto diventa saturo quando lo consuma sempre di più..
Esempio
Supponi di avere fame e di mangiare delle arance. Mangiare la prima arancia fornisce una grande utilità. L'utilità marginale della seconda arancia è sicuramente inferiore a quella della prima.
Allo stesso modo, l'utilità marginale della terza arancia è inferiore a quella della seconda e così via.
Dopo un certo stadio, l'utilità marginale diventa zero e oltre questo stadio diventa negativa. Questo perché si sazia man mano che vengono consumate sempre più arance..
Per capirlo meglio, puoi vedere la tabella 1. Le cifre sono ipotetiche e rappresentano l'utilità marginale del consumo di arance per una persona.
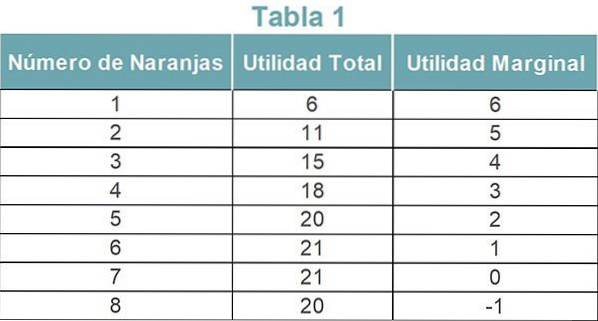
Profitto totale
L'utilità totale si ottiene aggiungendo l'utilità marginale di ciascuna unità di arancia consumata. Secondo la tabella 1, l'utilità totale delle prime sei arance è 21 (21 = 6 + 5 + 4 + 3 + 2 + 1).
Utilità marginale
L'utilità marginale dell'ennesima unità del prodotto è la differenza tra l'utilità totale dell'ennesima unità e l'utilità totale della (n-1) -esima unità del prodotto. UMn = UTn - UT (n-1) dove,
MUn = utilità marginale dell'ennesima unità.
UTn = Profitto totale dell'ennesima unità.
UT (n-1) = Profitto totale dell'unità (n-1) -esima.
Nell'esempio in Tabella 1, l'utilità marginale della quarta arancia è CU4 = TU4-TU3 = 18-15 = 3.
La figura seguente mostra in dettaglio le traiettorie delle curve di utilità totale e di utilità marginale.
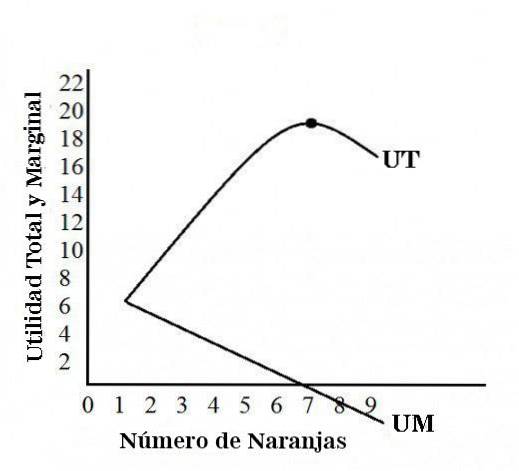
La curva di utilità totale inizialmente aumenta e, dopo un certo stadio, inizia a diminuire. È in questa fase che la curva di utilità marginale entra nella zona negativa..
La seconda legge di Gossen
La seconda legge dice che ogni persona spenderà i propri soldi in prodotti diversi, in modo che la quantità di tutti i piaceri sia uguale.
In questo modo, Gossen ha spiegato che il massimo godimento sarebbe stato raggiunto da un livello uniforme di soddisfazione. La seconda legge di Gossen è nota come legge dell'utilità equi-marginale.
Supponiamo che una persona possieda $ 200. La legge spiega come la persona alloca i $ 200 tra i loro diversi desideri per massimizzare la loro soddisfazione..
Il punto in cui la soddisfazione del consumatore è massima con le risorse date è noto come equilibrio del consumatore..
Esempio
Supponiamo che ci siano due prodotti X e Y. La risorsa del consumatore è $ 8. Il prezzo unitario del prodotto X è $ 1. Il prezzo unitario del prodotto Y è $ 1.
Il consumatore spende i suoi $ 8 acquistando il prodotto X. Poiché il prezzo unitario del prodotto X è $ 1, può acquistare 8 unità.
La tabella 2 mostra l'utilità marginale di ciascuna unità del prodotto X. Poiché la legge si basa sul concetto di utilità marginale decrescente, diminuisce con ogni unità successiva..
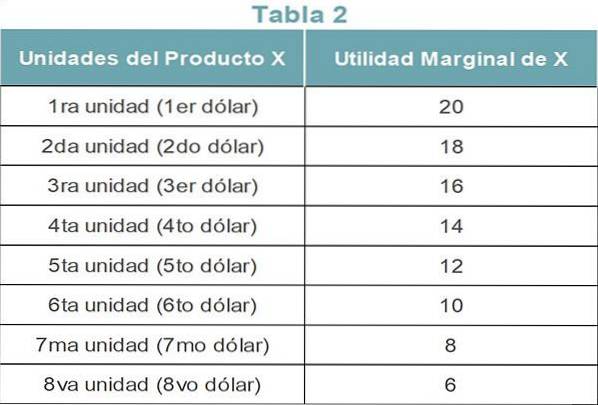
Consideriamo ora che il consumatore spende i suoi $ 8 acquistando il prodotto Y. La tabella 3 mostra l'utilità marginale di ciascuna unità di prodotto Y.
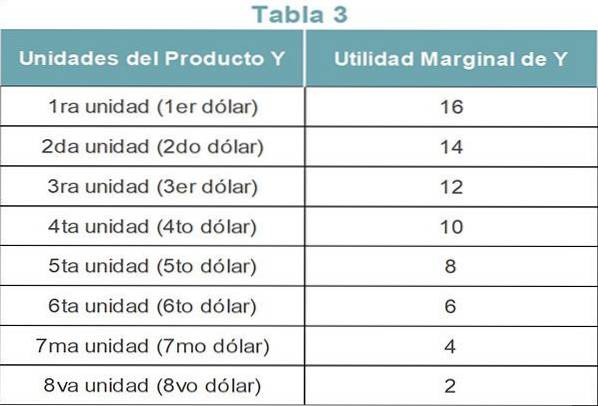
Se il consumatore prevede di allocare i suoi $ 8 tra il prodotto X e Y, la Tabella 4 mostra come il consumatore spende il suo reddito su entrambi i prodotti..
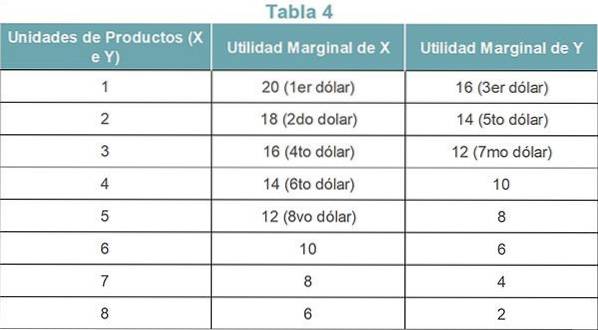
Applicazione della seconda legge
Poiché la prima unità del prodotto X dà il profitto più alto (20), spende il primo dollaro su X. Anche il secondo dollaro va al prodotto X, poiché dà 18, il secondo più alto.
Sia la prima unità del prodotto Y che la terza unità del prodotto X offrono la stessa quantità di profitto. Il consumatore preferisce acquistare il prodotto Y, perché ha già speso due dollari per il prodotto X.
Allo stesso modo, il quarto dollaro viene speso su X, il quinto dollaro su Y, il sesto dollaro su X, il settimo dollaro su Y e l'ottavo dollaro su X.
Pertanto, il consumatore acquista 5 unità di prodotto X e 3 unità di prodotto Y. Cioè, 5 unità di prodotto X e 3 unità di prodotto Y gli lasciano la migliore quantità di utilità totale.
Secondo la legge dell'utilità equi-marginale, il consumatore è in equilibrio a questo punto, sperimentando la massima soddisfazione. Per capirlo si può calcolare l'utilità totale dei prodotti consumati.
Profitto totale = UTx + UTy = (20 + 18 + 16 + 14 + 12) + (16 + 14 + 12) = 122. Qualsiasi altra combinazione di prodotti lascerebbe il cliente con un profitto totale inferiore.
Terza legge di Gossen
Questa legge indica che la scarsità è una precondizione necessaria per l'esistenza del valore economico. Cioè, un prodotto ha valore solo quando la sua domanda supera la sua offerta.
Usando la logica di Gossen, poiché l'utilità marginale diminuisce con il consumo, un prodotto può avere un'utilità marginale positiva o "valore" solo se l'offerta disponibile è inferiore a quella necessaria per generare sazietà. Altrimenti, il desiderio sarà saziato e quindi il suo valore sarà zero.
Gli argomenti di Gossen sul valore si basano sulle due leggi precedenti. Secondo lui, il valore è un termine relativo. Dipende dalla relazione tra l'oggetto e il soggetto.
All'aumentare della quantità, il valore di ciascuna unità aggiunta diminuisce, fino a diventare zero.
Riferimenti
- Kirti Shailes (2018). Prima e seconda legge del godimento umano di Gossen. Discussione di economia. Tratto da: economicsdiscussion.net.
- Sundaram Ponnusamy (2014). La legge dell'utilità marginale decrescente o prima legge di Gossen. Owlcation. Tratto da: owlcation.com.
- Sundaram Ponnusamy (2016). La legge dell'utilità equi-marginale o seconda legge di Gossen. Owlcation. Tratto da: owlcation.com.
- Concetti di economia (2015). Legge dell'utilità marginale decrescente. Tratto da: economicsconcepts.com.
- Wikipedia, l'enciclopedia libera (2018). Le leggi di Gossen. Tratto da: en.wikipedia.org.



Nessun utente ha ancora commentato questo articolo.