Il Legge di Ohm, nella sua forma macroscopica, indica che la tensione e l'intensità della corrente in un circuito sono direttamente proporzionali, essendo la resistenza la costante della proporzionalità. Denotando queste tre quantità rispettivamente come V, I e R, la legge di Ohm afferma che: V = I.R.
Allo stesso modo, la legge di Ohm è generalizzata per includere elementi circuitali che non sono puramente resistivi nei circuiti a corrente alternata, in questo modo assume la seguente forma: V = I. Z.
Dove Z è l'impedenza, che rappresenta anche l'opposizione al passaggio di corrente alternata da parte di un elemento del circuito, ad esempio un condensatore o un'induttanza.
Va notato che non tutti i materiali e gli elementi del circuito sono conformi alla legge di Ohm. Quelli in cui è valido sono chiamati elementi ohmico, e in cui non è adempiuto, lo sono non ohmico o non lineare.
Le resistenze elettriche comuni sono di tipo ohmico, ma diodi e transistor non lo sono, poiché la relazione tra tensione e corrente non è lineare in essi..
La legge di Ohm deve il suo nome al fisico e matematico tedesco di origine bavarese George Simon Ohm (1789-1854), che trascorse la sua carriera studiando il comportamento dei circuiti elettrici. L'unità per la resistenza elettrica nel Sistema Internazionale SI è stata chiamata in suo onore: l'ohm, che è espresso anche dalla lettera greca Ω.
Indice articolo
Sebbene la forma macroscopica della legge di Ohm sia la più conosciuta, poiché collega quantità facilmente misurabili in laboratorio, la forma microscopica mette in relazione due importanti grandezze vettoriali: il campo elettrico E e la densità di corrente J:
J = σ.E
Dove σ è la conduttività elettrica del materiale, una proprietà che indica quanto è facile condurre la corrente. Da parte sua J è un vettore la cui grandezza è il quoziente tra l'intensità di corrente I e l'area della sezione trasversale A attraverso la quale circola.
È logico supporre che esista una connessione naturale tra il campo elettrico all'interno di un materiale e la corrente elettrica che circola attraverso di esso, tale che maggiore è la corrente, maggiore è la corrente.
Ma la corrente non è un vettore, poiché non ha una direzione nello spazio. Invece il vettore J è perpendicolare -o normale- all'area della sezione trasversale del conduttore e la sua direzione è quella della corrente.
Da questa forma della legge di Ohm si arriva alla prima equazione, assumendo un conduttore di lunghezza ℓ e sezione A, e sostituendo le grandezze di J Y E per:
J = I / A
E = V / ℓ
J = σ.E → I / A = σ. (V / ℓ)
V = (ℓ / σ.A) .I
Viene chiamato l'inverso della conduttività resistività ed è indicato dalla lettera greca ρ:
1 / σ = ρ
Perciò:
V = (ρℓ / A) .I = R.I
Nell'equazione V = (ρℓ / A) .I, la costante (ρℓ / A) è la resistenza, quindi:
R = ρℓ / A
La resistenza del conduttore dipende da tre fattori:
-La sua resistività ρ, tipica del materiale con cui è realizzato.
-La lunghezza ℓ.
-L'area A della sua sezione trasversale.
Maggiore è ℓ, maggiore è la resistenza, poiché i portatori di corrente hanno maggiori possibilità di scontrarsi con altre particelle all'interno del conduttore e perdere energia. E al contrario, più A è alto, più è facile per i portatori attuali muoversi in modo ordinato attraverso il materiale..
Infine, nella struttura molecolare di ogni materiale risiede la facilità con cui una sostanza lascia passare la corrente elettrica. Così, ad esempio, metalli come rame, oro, argento e platino, con bassa resistività, sono buoni conduttori, mentre legno, gomma e olio non lo sono, motivo per cui hanno una resistività maggiore.
Ecco due esempi illustrativi della legge di Ohm.
Una semplice esperienza illustra la legge di Ohm, per questo è necessario un pezzo di materiale conduttivo, una sorgente di tensione variabile e un multimetro.
Viene stabilita una tensione V tra le estremità del materiale conduttivo, che deve essere variata a poco a poco. Con il generatore variabile è possibile impostare i valori di detta tensione, che vengono misurati con il multimetro, nonché la corrente I che circola nel conduttore..
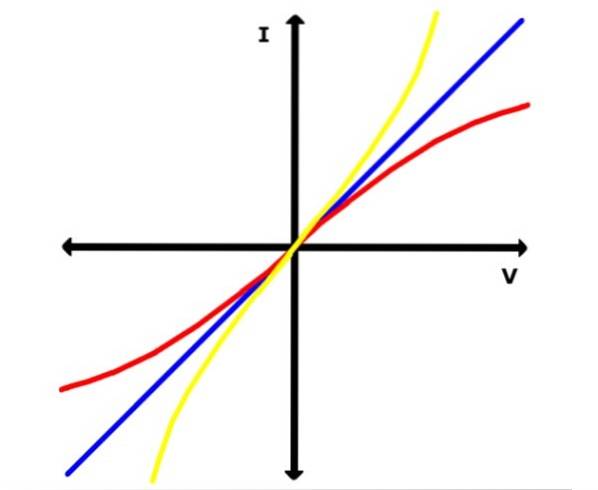
Le coppie di valori V e I vengono registrate in una tabella e con esse viene costruito un grafico su carta millimetrata. Se la curva risultante è una linea retta, il materiale è ohmico, ma se è qualsiasi altra curva, il materiale non è ohmico.
Nel primo caso si può determinare la pendenza della linea, che è equivalente alla resistenza R del conduttore o al suo inverso, la conduttanza.
Nell'immagine sotto, la linea blu rappresenta uno di questi grafici per un materiale ohmico. Nel frattempo, le curve gialle e rosse sono fatte di materiali non ohmici, come un semiconduttore, per esempio..
È interessante sapere che la corrente elettrica nella legge di Ohm si comporta in modo simile a quella dell'acqua che scorre attraverso un tubo. Il fisico inglese Oliver Lodge fu il primo a proporre la simulazione del comportamento della corrente utilizzando elementi di idraulica.
Ad esempio, i tubi rappresentano i conduttori, poiché l'acqua circola attraverso di essi e i portatori di corrente attraverso questi ultimi. Quando c'è una costrizione nel tubo, il passaggio dell'acqua è difficile, quindi questo equivarrebbe a una resistenza elettrica.
La differenza di pressione alle due estremità del tubo consente all'acqua di fluire, che fornisce un dislivello o una pompa dell'acqua, e allo stesso modo, la differenza di potenziale (la batteria) è ciò che mantiene la carica in movimento., Equivalente al flusso o volume d'acqua per unità di tempo.
Una pompa a pistone svolgerebbe il ruolo di una sorgente di tensione alternata, ma il vantaggio di mettere su una pompa dell'acqua è che il circuito idraulico sarebbe quindi chiuso, proprio come deve essere un circuito elettrico perché la corrente possa fluire.
L'equivalente di un interruttore in un circuito, sarebbe un rubinetto. Viene interpretato in questo modo: se il circuito è aperto (rubinetto chiuso), la corrente, come l'acqua, non può fluire.
Con interruttore chiuso (rubinetto tutto aperto) invece sia la corrente che l'acqua possono fluire senza problemi attraverso il conduttore o il tubo.
Il rubinetto o la valvola può anche rappresentare una resistenza: quando il rubinetto è completamente aperto, equivale ad avere una resistenza nulla o un cortocircuito. Se chiude completamente è come avere il circuito aperto, mentre parzialmente chiuso è come avere una resistenza di un certo valore (vedi figura 3).
È noto che un ferro da stiro elettrico richiede 2 A a 120 V per funzionare correttamente. Qual è la tua resistenza?
Risolvi per la resistenza dalla legge di Ohm:
R = V / I = 120 V / 2 A = 60 Ω
Un filo con un diametro di 3 mm e una lunghezza di 150 m ha una resistenza elettrica di 3,00 Ω a 20 ° C. Trova la resistività del materiale.
L'equazione R = ρℓ / A è appropriato, quindi l'area della sezione trasversale deve essere trovata prima:
A = π(D / 2)Due = π (3 x 10-3 m / 2)Due = 4,5π x 10 -6 mDue
Infine, quando si sostituisce si ottiene:
ρ = A.R / ℓ = 4,5π x 10 -6 mDue x 3 Ω / 150 m = 2,83 x 10 -7 Ω.m
Nessun utente ha ancora commentato questo articolo.