Il Legge di Coulomb è la legge fisica che governa l'interazione tra oggetti caricati elettricamente. Fu enunciato dallo scienziato francese Charles Augustin de Coulomb (1736-1806), grazie ai risultati dei suoi esperimenti con la bilancia di torsione.
Nel 1785, Coulomb sperimentò innumerevoli volte con piccole sfere caricate elettricamente, ad esempio spostando due sfere più vicine o più lontane, variando l'entità della loro carica e anche il loro segno. Osservando e registrando sempre attentamente ogni risposta.
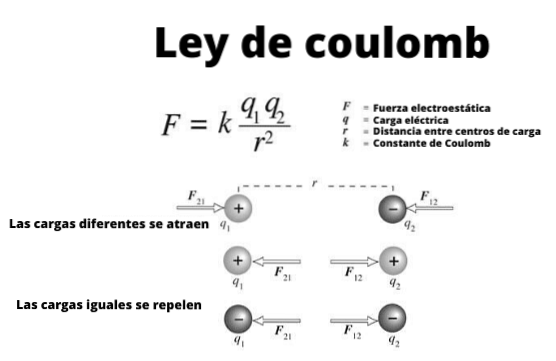
Queste piccole sfere possono essere considerate come punti di carico, cioè oggetti le cui dimensioni sono insignificanti. E realizzano, come è noto sin dai tempi degli antichi Greci, che le cariche dello stesso segno respingono e quelle di un segno diverso si attraggono..
Con questo in mente, Charles Coulomb ha trovato quanto segue:
-La forza attrattiva o repulsiva tra due cariche puntuali è direttamente proporzionale al prodotto della grandezza delle cariche.
-Questa forza è sempre diretta lungo la linea che unisce le cariche.
-Infine, l'entità della forza è inversamente proporzionale al quadrato della distanza tra le cariche.
Indice articolo
Grazie a queste osservazioni, Coulomb ha concluso che l'entità della forza F tra due cariche puntiformi che cosa1 Y che cosaDue, separato una distanza r, è matematicamente dato come:
Poiché la forza è una grandezza vettoriale, per esprimerla completamente si definisce un vettore unitario r nella direzione della linea che unisce le cariche (un vettore unitario ha magnitudine uguale a 1).
Inoltre, la costante di proporzionalità necessaria per trasformare l'espressione precedente in un'uguaglianza è chiamata ke o semplicemente k: il costante elettrostatica o Costante di Coulomb.
Infine, la legge di Coulomb è stabilita per le cariche di punti, data da:
La forza, come sempre nel Sistema internazionale di unità, arriva in newton (N). Per quanto riguarda le cariche, l'unità è denominata coulomb (C) in onore di Charles Coulomb e infine la distanza r è espressa in metri (m).
Osservando attentamente l'equazione di cui sopra, è chiaro che la costante elettrostatica deve avere unità di N.mDue / CDue, per ottenere newton come risultato. Il valore della costante è stato determinato sperimentalmente come:
Ke = 8,89 x 10 9 N.mDue / CDue ≈ 9 x 10 9 N.mDue / CDue
La figura 1 illustra l'interazione tra due cariche elettriche: quando sono dello stesso segno si respingono, altrimenti si attraggono.
Si noti che la legge di Coulomb è conforme alla terza legge di Newton o legge di azione e reazione, quindi le grandezze di F1 Y FDue sono la stessa cosa, la direzione è la stessa, ma i sensi sono opposti.
Per risolvere problemi di interazione tra cariche elettriche occorre tenere in considerazione quanto segue:
- L'equazione si applica esclusivamente nel caso di cariche puntiformi, cioè oggetti caricati elettricamente ma di dimensioni molto piccole. Se gli oggetti caricati hanno dimensioni misurabili, è necessario dividerli in carichi molto piccoli e quindi aggiungere i contributi di ciascuno di questi carichi, per i quali è richiesto un calcolo integrale..
- La forza elettrica è una quantità vettoriale. Se ci sono più di due cariche interagenti, la forza netta sulla carica qio è dato dal principio di sovrapposizione:
Fnetto = Fi1 + Fi2 + Fi3 + Fi4 +… = ∑ Fij
Dove il pedice j è uguale a 1, 2, 3, 4 ... e rappresenta ciascuna delle cariche rimanenti.
- Dovresti sempre essere coerente con le unità. La cosa più frequente è lavorare con la costante elettrostatica nelle unità SI, quindi è necessario assicurarsi che le cariche siano in coulomb e le distanze in metri.
- Infine, l'equazione si applica quando le cariche sono in equilibrio statico.
Nella figura seguente ci sono due cariche puntiformi + q e + 2q. Un terzo punto di carica -q è posto in P. Si chiede di trovare la forza elettrica su questa carica per la presenza delle altre.
La prima cosa è stabilire un sistema di riferimento adeguato, che in questo caso è l'asse orizzontale o l'asse x. L'origine di un tale sistema può essere ovunque, ma per comodità sarà posta in P, come mostrato nella figura 4a:
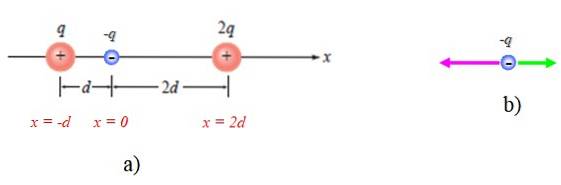
Viene anche mostrato un diagramma delle forze su -q, tenendo conto che è attratto dalle altre due (figura 4b).
Chiamiamo F1 le forze esercitate dalla carica q sulla carica -q, sono dirette lungo l'asse xe puntano in direzione negativa, quindi:
Analogamente, viene calcolato FDue:
Notare che la grandezza di FDue è la metà di quello di F1, sebbene il carico sia doppio. Per trovare la forza netta, infine, vengono aggiunti vettorialmente F1 Y FDue:
Fnetto = (-k + k / 2). (qDue / dDue) (X) N = - (k / 2). (QDue / dDue) (X) N
Due palline di polistirolo di uguale massa m = 9,0 x 10-8 kg hanno la stessa carica positiva Q e sono sospesi da un filo di seta di lunghezza L = 0,98 m. Le sfere sono separate da una distanza di d = 2 cm. Calcola il valore di Q.
La situazione dell'istruzione è descritta nella figura 5a.
Scegliamo una delle sfere e su di essa disegniamo il diagramma del corpo isolato, che comprende tre forze: il peso W, tensione nella corda T e repulsione elettrostatica F, come appare nella figura 5b. E ora i passaggi:
Il valore di θ / 2 è calcolato con il triangolo in figura 5c:
θ / 2 = arcsen (1 x 10-Due/ 0,98) = 0,585º
Successivamente dobbiamo applicare la seconda legge di Newton e impostarla uguale a 0, poiché le cariche sono in equilibrio statico. È importante sottolineare che la tensione T è inclinato e ha due componenti:
∑FX = -T.sin θ + F = 0
∑FY = T.cos θ - W = 0
Risolviamo per l'entità dello stress dall'ultima equazione:
T = W / cos θ = mg / cos θ
Questo valore viene sostituito nella prima equazione per trovare la grandezza di F:
F = T sin θ = mg (sin θ / cos θ) = mg. tg θ
Poiché F = k QDue / dDue, cancella Q:
Q = 2 × 10-undici C.
Controllare la legge di Coulomb è facile usando una bilancia di torsione simile a quella usata da Coulomb nel suo laboratorio..
Sono presenti due piccole sfere di sambuco, una delle quali, quella al centro della bilancia, è sospesa da un filo. L'esperimento consiste nel toccare le sfere di sambuco scariche con un'altra sfera metallica carica di carica Q..
Immediatamente la carica viene distribuita equamente tra le due sfere di sambuco, ma poi, essendo cariche dello stesso segno, si respingono a vicenda. Sulla sfera sospesa agisce una forza che provoca la torsione del filo da cui pende e si allontana immediatamente dalla sfera fissa.
Quindi vediamo che oscilla alcune volte fino a raggiungere l'equilibrio. Quindi la torsione dell'asta o del filo che lo trattiene è bilanciata dalla forza di repulsione elettrostatica.
Se originariamente le sfere erano a 0º, ora la sfera in movimento avrà ruotato di un angolo θ. Attorno alla scala c'è un nastro graduato in gradi per misurare questo angolo. Determinando preventivamente la costante di torsione, si calcola facilmente la forza repulsiva e il valore della carica acquisita dalle sfere di sambuco.
Nessun utente ha ancora commentato questo articolo.