
Caratteristiche delle lenti convergenti, tipologie ed esercizio risolto
Il lenti convergenti Sono quelli più spessi nella parte centrale e più sottili ai bordi. Di conseguenza, concentrano (convergono) i raggi di luce che cadono su di essi parallelamente all'asse principale in un unico punto. Questo punto è chiamato fuoco, o fuoco dell'immagine, ed è rappresentato dalla lettera F. Le lenti convergenti o positive formano quelle che vengono chiamate immagini reali di oggetti..
Un tipico esempio di lente convergente è una lente d'ingrandimento. Tuttavia, è comune trovare questo tipo di lente in dispositivi molto più complessi come microscopi o telescopi. In effetti, un microscopio composto di base è costituito da due lenti convergenti che hanno una piccola lunghezza focale. Queste lenti sono chiamate oggettive e oculari.

Le lenti convergenti sono utilizzate nell'ottica per diverse applicazioni, anche se forse la più nota è quella di correggere i difetti visivi. Pertanto, sono indicati per trattare l'ipermetropia, la presbiopia e anche alcuni tipi di astigmatismo come l'astigmatismo ipermetrope.
Indice articolo
- 1 Caratteristiche
- 2 Elementi convergenti dell'obiettivo
- 3 Formazione dell'immagine in lenti convergenti
- 4 tipi di lenti convergenti
- 5 Differenza con lenti divergenti
- 6 equazioni gaussiane di lenti sottili e ingrandimento di una lente
- 6.1 Equazione gaussiana
- 6.2 Ingrandimento di una lente
- 7 Esercizio risolto
- 8 Riferimenti
Caratteristiche
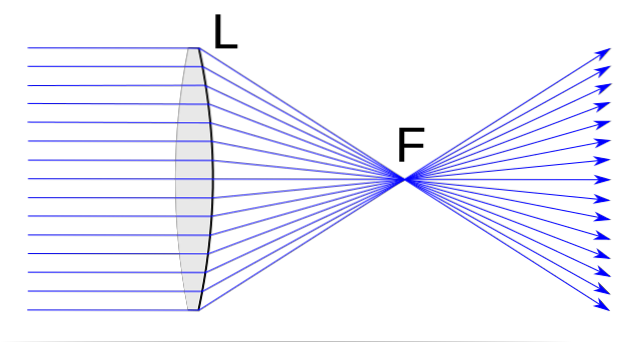
Le lenti convergenti hanno una serie di caratteristiche distintive. In ogni caso, forse il più importante è quello che abbiamo già avanzato nella sua definizione. Pertanto, le lenti convergenti sono caratterizzate dal deflettere attraverso il fuoco qualsiasi raggio che cade su di esse in una direzione parallela all'asse principale.
Inoltre, reciprocamente, qualsiasi raggio incidente che passa il fuoco viene rifratto parallelamente all'asse ottico della lente..
Elementi convergenti delle lenti
Per il suo studio è importante sapere quali elementi costituiscono le lenti in generale e le lenti convergenti in particolare..
In generale, è chiamato il centro ottico di una lente al punto in cui ogni raggio che la attraversa non subisce alcuna deviazione..
L'asse principale è la linea che unisce il centro ottico e il fuoco principale, che abbiamo già commentato, è rappresentato dalla lettera F.
L'obiettivo principale è il punto in cui tutti i raggi che colpiscono l'obiettivo sono paralleli all'asse principale..
La lunghezza focale è la distanza tra il centro ottico e il fuoco..
I centri di curvatura sono definiti come i centri delle sfere che creano la lente; i raggi di curvatura sono i raggi delle sfere che danno origine alla lente.
Infine, il piano centrale dell'obiettivo è chiamato piano ottico..
Formazione dell'immagine in lenti convergenti
Per quanto riguarda la formazione delle immagini in lenti convergenti, occorre tenere conto di una serie di regole di base, che vengono spiegate di seguito..
Se il raggio colpisce la lente parallelamente all'asse, il raggio emergente converge sulla messa a fuoco dell'immagine. Al contrario, se un raggio incidente passa attraverso il fuoco dell'oggetto, il raggio emerge in una direzione parallela all'asse. Infine, i raggi che passano attraverso il centro ottico vengono rifratti senza subire alcun tipo di deflessione..
Di conseguenza, in una lente convergente possono verificarsi le seguenti situazioni:
- Che l'oggetto si trovi rispetto al piano ottico ad una distanza maggiore del doppio della lunghezza focale. In questo caso, l'immagine prodotta è reale, invertita e più piccola dell'oggetto..
- Che l'oggetto si trovi ad una distanza dal piano ottico pari al doppio della lunghezza focale. Quando ciò accade, l'immagine che si ottiene è un'immagine reale, invertita e della stessa dimensione dell'oggetto.
- Che l'oggetto si trovi a una distanza dal piano ottico compresa tra una e il doppio della lunghezza focale. Quindi, viene prodotta un'immagine reale, invertita e più grande dell'oggetto originale..
- Che l'oggetto si trovi a una distanza dal piano ottico inferiore alla lunghezza focale. In tal caso, l'immagine sarà virtuale, diretta e più grande dell'oggetto.
Tipi di lenti convergenti
Esistono tre diversi tipi di lenti convergenti: lenti biconvesse, lenti piano-convesse e lenti concave-convesse..
Le lenti biconvesse, come suggerisce il nome, sono composte da due superfici convesse. I piani convessi, nel frattempo, hanno una superficie piatta e una convessa. Infine, le lenti convesse concave sono costituite da una superficie leggermente concava e da una convessa..
Differenza con lenti divergenti

Le lenti divergenti, invece, differiscono dalle lenti convergenti in quanto lo spessore diminuisce dai bordi verso il centro. Quindi, contrariamente a quanto accaduto con le lenti convergenti, in questo tipo di lenti si separano i raggi luminosi che colpiscono parallelamente all'asse principale. In questo modo, formano quelle che vengono chiamate immagini virtuali di oggetti.
In ottica, lenti divergenti o negative, come sono anche note, vengono utilizzate principalmente per correggere la miopia.
Equazioni gaussiane di lenti sottili e ingrandimento di una lente
In generale, il tipo di lenti che vengono studiate sono quelle che vengono chiamate lenti sottili. Sono definiti come quelli che hanno uno spessore ridotto rispetto ai raggi di curvatura delle superfici che li limitano.
Questo tipo di lente può essere studiato con l'equazione gaussiana e con l'equazione che permette di determinare l'ingrandimento di una lente.
Equazione di Gauss
L'equazione gaussiana per lenti sottili può essere utilizzata per risolvere una moltitudine di problemi nell'ottica di base. Da qui la sua grande importanza. La sua espressione è la seguente:
1 / f = 1 / p + 1 / q
Dove 1 / f è la cosiddetta potenza di un obiettivo ef è la lunghezza focale o la distanza dal centro ottico al fuoco F.L'unità di misura della potenza di una lente è la diottria (D), dove 1 D = 1 m-1. D'altra parte, p e q sono rispettivamente la distanza alla quale si trova un oggetto e la distanza alla quale viene osservata la sua immagine.
Ingrandimento di una lente
L'ingrandimento laterale di una lente sottile si ottiene con la seguente espressione:
M = - q / p
Dove M è l'ingrandimento. Dal valore dell'aumento si possono dedurre una serie di conseguenze:
Sì | M | > 1, la dimensione dell'immagine è maggiore di quella dell'oggetto
Sì | M | < 1, el tamaño de la imagen es menor que el del objeto
Se M> 0, l'immagine è a destra e sullo stesso lato della lente dell'oggetto (immagine virtuale)
Si m < 0, la imagen está invertida y en el lado contrario que el objeto (imagen real)
Esercizio risolto
Un corpo si trova a un metro di distanza da una lente convergente, che ha una lunghezza focale di 0,5 metri. Come sarà l'immagine del corpo? Quanto lontano sarai?
Abbiamo i seguenti dati: p = 1 m; f = 0,5 m.
Inseriamo questi valori nell'equazione gaussiana per lenti sottili:
1 / f = 1 / p + 1 / q
E rimane il seguente:
1 / 0,5 = 1 + 1 / q; 2 = 1 + 1 / q
Isoliamo 1 / q
1 / q = 1
Per risolvere quindi per q e ottenere:
q = 1
Quindi, sostituiamo nell'equazione l'ingrandimento di una lente:
M = - q / p = -1 / 1 = -1
Pertanto, l'immagine è reale poiché q> 0, invertita perché M < 0 y de igual tamaño dado que el valor absoluto de M es 1. Por último, la imagen se encuentra a un metro de distancia del foco.
Riferimenti
- Leggero (n.d.). Su Wikipedia. Estratto il 18 marzo 2019 da es.wikipedia.org.
- Lekner, John (1987). Teoria della riflessione, delle onde elettromagnetiche e delle particelle. Springer.
- Leggero (n.d.). In Wikipedia. Estratto il 20 marzo 2019 da en.wikipedia.org.
- Obiettivo (n.d.). Su Wikipedia. Estratto il 17 marzo 2019 da es.wikipedia.org.
- Obiettivo (ottica). In Wikipedia. Estratto il 19 marzo 2019 da en.wikipedia.org.
- Hecht, Eugene (2002). Ottica (4a ed.). Addison Wesley.
- Tipler, Paul Allen (1994). Fisico. 3a edizione. Barcellona: ho invertito.


Nessun utente ha ancora commentato questo articolo.