Formule di induzione magnetica, come si calcola ed esempi

Il induzione magnetica o la densità del flusso magnetico è un'alterazione dell'ambiente causata dalla presenza di correnti elettriche. Modificano la natura dello spazio che li circonda, creando a campagna vettore.

Il vettore induzione magnetica, densità del flusso magnetico O semplicemente campo magnetico B, ha tre caratteristiche distintive: un'intensità espressa da un valore numerico, una direzione e anche un senso dato in ogni punto dello spazio. È evidenziato in grassetto per distinguerlo da quantità puramente numeriche o scalari.

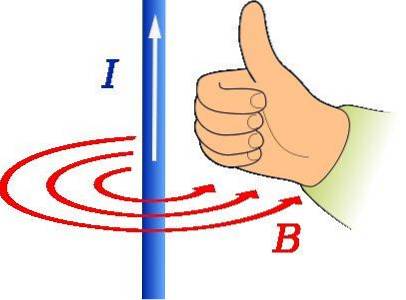
La regola del pollice destro viene utilizzata per trovare la direzione e la direzione del campo magnetico causato da un filo che trasporta corrente, come mostrato nella figura sopra.

Il pollice della mano destra dovrebbe puntare nella direzione della corrente. Quindi la rotazione delle quattro dita rimanenti indica la forma di B, che in figura è rappresentato dai cerchi concentrici rossi.

In tal caso, l'indirizzo di B è tangenziale alla circonferenza concentrica al filo ed è antiorario.

Il induzione magnetica B Nel Sistema Internazionale si misura Tesla (T), tuttavia è più frequente misurarlo in un'altra unità chiamata Gauss (G). Entrambe le unità furono chiamate rispettivamente in onore di Nikola Tesla (1856-1943) e Carl Friedrich Gauss (1777-1855) per i loro straordinari contributi alla scienza dell'elettricità e del magnetismo..

Indice articolo

• 1 Quali sono le proprietà dell'induzione magnetica o della densità del flusso magnetico?
• 2 Legge di Biot-Savart
• 3 formule
• 4 Come viene calcolato?
  • 4.1 Esempio
• 5 Riferimenti

Quali sono le proprietà dell'induzione magnetica o della densità del flusso magnetico?

Una bussola posizionata vicino a un filo sotto tensione sarà sempre allineata con B. Il fisico danese Hans Christian Oersted (1777-1851) fu il primo a notare questo fenomeno all'inizio del XIX secolo.

E quando la corrente cessa, la bussola punta di nuovo verso il nord geografico, come sempre. Modificando accuratamente la posizione della bussola, si ottiene una mappa della forma del campo magnetico.

Questa mappa ha sempre la forma di cerchi concentrici al filo, come descritto all'inizio. In questo modo puoi visualizzare B.

Anche se il filo non è dritto, il vettore B formerà cerchi concentrici attorno ad esso. Per determinare la forma del campo, basta immaginare segmenti di filo molto piccoli, così piccoli da apparire rettilinei e circondati da cerchi concentrici..

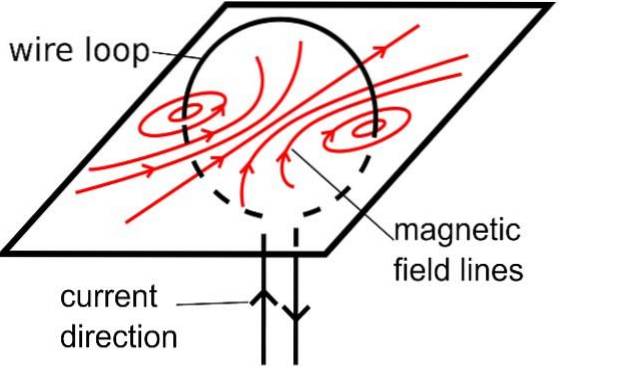
Ciò indica un'importante proprietà delle linee del campo magnetico. B: non hanno inizio né fine, sono sempre curve chiuse.

Legge di Biot-Savart

Il 19 ° secolo ha segnato l'inizio dell'era dell'elettricità e del magnetismo nella scienza. Intorno all'anno 1820 i fisici francesi Jean Marie Biot (1774-1862) e Felix Savart (1791-1841) scoprirono la legge che porta il loro nome e che ci permette di calcolare il vettore B.

Hanno fatto le seguenti osservazioni sul contributo al campo magnetico prodotto da un segmento di filo di lunghezza differenziale dl che trasporta una corrente elettrica io:

• La grandezza di B diminuisce con il quadrato inverso della distanza dal filo (questo ha senso: lontano dal filo l'intensità di B deve essere inferiore a punti vicini).
• La grandezza di B è proporzionale all'intensità della corrente io che passa attraverso il filo.
• L'indirizzo di B è tangenziale alla circonferenza del raggio r centrato sul filo e il senso di B è dato, come abbiamo detto, dalla regola del pollice destro.

Il prodotto incrociato o prodotto incrociato è lo strumento matematico appropriato per esprimere l'ultimo punto. Per stabilire un prodotto vettoriale, sono necessari due vettori, definiti come segue:

• dl è il vettore la cui grandezza è la lunghezza del segmento differenziale dl
• r è il vettore che va dal filo al punto in cui vuoi trovare il campo

Formule

Tutto questo può essere combinato in un'espressione matematica:

La costante di proporzionalità necessaria per stabilire l'uguaglianza è la permeabilità magnetica dello spazio libero μ_o  = 4π.10^-7 T.m / A

Questa espressione è la legge di Biot e Savart, che ci permette di calcolare il campo magnetico di un segmento di corrente.

Tale segmento a sua volta deve far parte di un circuito più ampio e più chiuso: una distribuzione di corrente.

La condizione che il circuito sia chiuso è necessaria per il flusso di corrente elettrica. La corrente elettrica non può fluire in circuiti aperti.

Infine, per trovare il campo magnetico totale di detta distribuzione di corrente, vengono sommati tutti i contributi di ciascun segmento differenziale dl. Ciò equivale a integrare sull'intera distribuzione:

Per applicare la legge di Biot-Savart e calcolare il vettore di induzione magnetica, è necessario considerare alcuni punti importanti molto importanti:

• Il prodotto incrociato tra due vettori si traduce sempre in un altro vettore.

• 

• È conveniente trovare il prodotto vettoriale prima per passare alla risoluzione dell'integrale si risolve poi l'integrale di ciascuna delle componenti ottenute separatamente.
• È necessario disegnare un'immagine della situazione e stabilire un sistema di coordinate adatto.
• Ogni volta che si osserva l'esistenza di una certa simmetria, dovrebbe essere utilizzata per risparmiare tempo di calcolo.
• Quando ci sono triangoli, il teorema di Pitagora e il teorema del coseno sono di grande aiuto per stabilire la relazione geometrica tra le variabili.

Come viene calcolato?

Con un esempio pratico del calcolo di B per un cavo diritto, si applicano queste raccomandazioni.

Esempio

Calcola il vettore del campo magnetico che un filo rettilineo molto lungo produce in un punto P nello spazio, secondo la figura mostrata.

Dalla figura devi:

• Il filo è diretto in direzione verticale, con la corrente che scorre verso l'alto. Questa direzione è + y nel sistema di coordinate, la cui origine è nel punto O.

• 

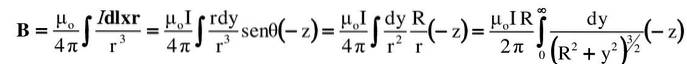
• In tal caso, secondo la regola del pollice destro, B al punto P è rivolto verso l'interno della carta, per questo è indicato da un piccolo cerchio e da una “x” nella figura. Questo indirizzo verrà preso come -z.
• Il triangolo rettangolo le cui gambe sono Y Y R, mettere in relazione entrambe le variabili secondo il teorema di Pitagora: r^Due= R^Due+Y^Due

Tutto questo è sostituito nell'integrale. Il prodotto incrociato o croce è indicato dalla sua grandezza più la sua direzione e il suo senso:

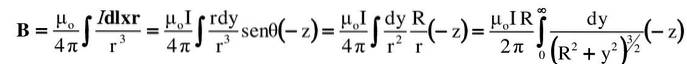
L'integrale proposto si trova in una tabella di integrali oppure viene risolto con una opportuna sostituzione trigonometrica (il lettore può verificare il risultato utilizzando y = Rtg θ):

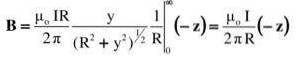
Il risultato concorda con quanto ci si aspettava: l'ampiezza del campo diminuisce con la distanza R e aumenta proporzionalmente con l'intensità della corrente I.

Sebbene un filo infinitamente lungo sia un'idealizzazione, l'espressione ottenuta è un'ottima approssimazione per il campo di un filo lungo.

Con la legge di Biot e Savart è possibile trovare il campo magnetico di altre distribuzioni altamente simmetriche, come un anello circolare che trasporta corrente, o fili piegati che combinano segmenti rettilinei e curvilinei..

Naturalmente, per risolvere analiticamente l'integrale proposto, il problema deve avere un alto grado di simmetria. Altrimenti l'alternativa è risolvere numericamente l'integrale.

Riferimenti

1. Serway, R., Jewett, J. (2008). Fisica per la scienza e l'ingegneria. Volume 2. Messico. Cengage Learning Editors. 367-372.