Il omoschedasticità in un modello statistico predittivo si verifica se in tutti i gruppi di dati di una o più osservazioni, la varianza del modello rispetto alle variabili esplicative (o indipendenti) rimane costante.
Un modello di regressione può essere omoschedastico o no, nel qual caso si parla di eteroschedasticità.
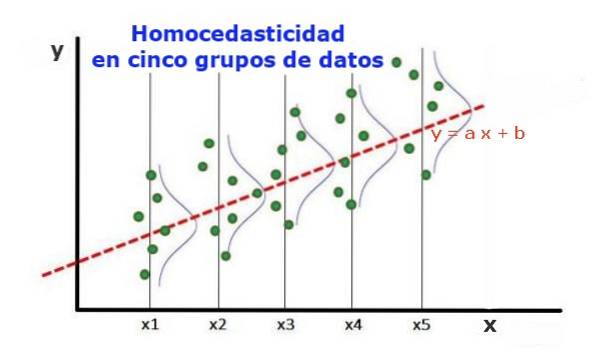
Un modello di regressione statistica di più variabili indipendenti è chiamato omoscedastico, solo se la varianza dell'errore della variabile prevista (o la deviazione standard della variabile dipendente) rimane uniforme per i diversi gruppi di valori delle variabili esplicative o indipendenti.
Nei cinque gruppi di dati della Figura 1, è stata calcolata la varianza in ciascun gruppo, rispetto al valore stimato dalla regressione, risultando uguale in ciascun gruppo. Si presume inoltre che i dati seguano la distribuzione normale.
A livello grafico, significa che i punti sono ugualmente dispersi o dispersi attorno al valore previsto dall'adattamento di regressione e che il modello di regressione ha lo stesso errore e validità per l'intervallo della variabile esplicativa..
Indice articolo
Per illustrare l'importanza dell'omoscedasticità nella statistica predittiva, è necessario contrastare il fenomeno opposto, l'eteroscedasticità.
Nel caso della figura 1, in cui è presente l'omoschedasticità, è vero che:
Var ((y1-Y1); X1) ≈ Var ((y2-Y2); X2) ≈… Var ((y4-Y4); X4)
Dove Var ((yi-Yi); Xi) rappresenta la varianza, la coppia (xi, yi) rappresenta i dati del gruppo i, mentre Yi è il valore previsto dalla regressione per il valore medio Xi del gruppo. La varianza degli n dati del gruppo i viene calcolata come segue:
Var ((yi-Yi); Xi) = ∑j (yij - Yi) ^ 2 / n
Al contrario, quando si verifica l'eteroscedasticità, il modello di regressione potrebbe non essere valido per l'intera regione in cui è stato calcolato. La figura 2 mostra un esempio di questa situazione.
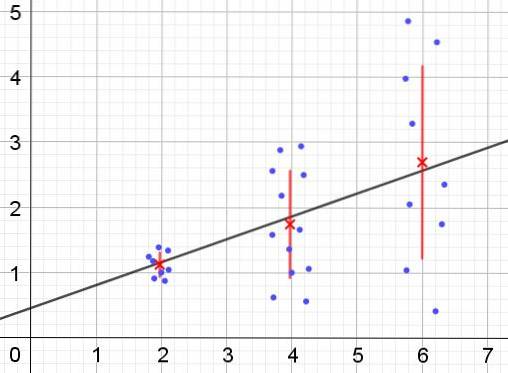
La Figura 2 rappresenta tre gruppi di dati e l'adattamento dell'insieme utilizzando una regressione lineare. Va notato che i dati nel secondo e nel terzo gruppo sono più dispersi rispetto al primo gruppo. Il grafico in figura 2 mostra anche il valore medio di ogni gruppo e la sua barra di errore ± σ, con la deviazione standard σ di ogni gruppo di dati. Va ricordato che la deviazione standard σ è la radice quadrata della varianza.
È chiaro che nel caso dell'eteroscedasticità, l'errore di stima della regressione sta cambiando nell'intervallo di valori della variabile esplicativa o indipendente e negli intervalli in cui questo errore è molto grande, la previsione della regressione è inaffidabile o non applicabile.
In un modello di regressione gli errori o residui (e -Y) devono essere distribuiti con uguale varianza (σ ^ 2) nell'intervallo di valori della variabile indipendente. È per questo motivo che un buon modello di regressione (lineare o non lineare) deve superare il test di omoscedasticità..
I punti riportati in figura 3 corrispondono ai dati di uno studio che cerca una relazione tra i prezzi (in dollari) delle case in funzione delle dimensioni o della superficie in metri quadrati.
Il primo modello da testare è quello della regressione lineare. In primo luogo, si nota che il coefficiente di determinazione R ^ 2 dell'adattamento è piuttosto alto (91%), quindi si può pensare che l'adattamento sia soddisfacente..
Tuttavia, due regioni possono essere chiaramente distinte dal grafico di aggiustamento. Uno di loro, quello a destra racchiuso in un ovale, soddisfa l'omoscedasticità, mentre la regione a sinistra non ha l'omoschedasticità.
Ciò significa che la previsione del modello di regressione è adeguata e affidabile nell'intervallo compreso tra 1800 m ^ 2 e 4800 m ^ 2 ma molto inadeguata al di fuori di questa regione. Nella zona eteroschedastica, non solo l'errore è molto ampio, ma anche i dati sembrano seguire un andamento diverso da quello proposto dal modello di regressione lineare..
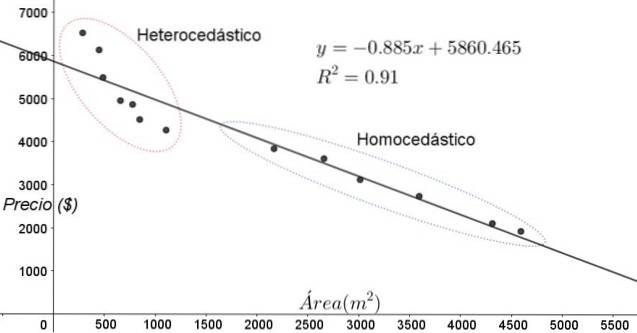
Lo scatter plot dei dati è il test più semplice e visivo della loro omoschedasticità, tuttavia nelle occasioni in cui non è così evidente come nell'esempio mostrato in figura 3, è necessario ricorrere a grafici con variabili ausiliarie..
Per separare le aree in cui l'omoschedasticità è soddisfatta e in cui non lo è, vengono introdotte le variabili standardizzate ZRes e ZPred:
ZRes = Abs (y - Y) / σ
ZPred = Y / σ
Va notato che queste variabili dipendono dal modello di regressione applicato, poiché Y è il valore della previsione di regressione. Di seguito è riportato il grafico a dispersione ZRes vs ZPred per lo stesso esempio:
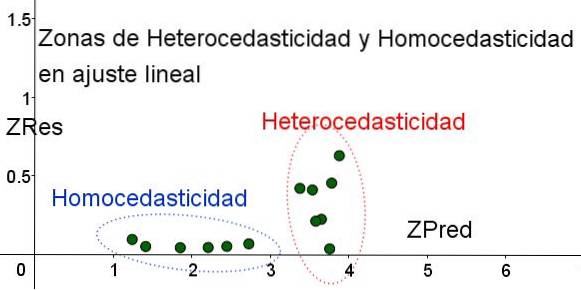
Nel grafico di Figura 4 con le variabili standardizzate, l'area in cui l'errore residuo è piccolo e uniforme è chiaramente separata dall'area in cui non lo è. Nella prima zona, l'omoschedasticità è soddisfatta mentre nella regione in cui l'errore residuo è molto variabile e grande, l'eteroscedasticità è soddisfatta..
L'aggiustamento della regressione è applicato allo stesso gruppo di dati nella figura 3, in questo caso l'aggiustamento è non lineare, poiché il modello utilizzato coinvolge una potenziale funzione. Il risultato è mostrato nella figura seguente:
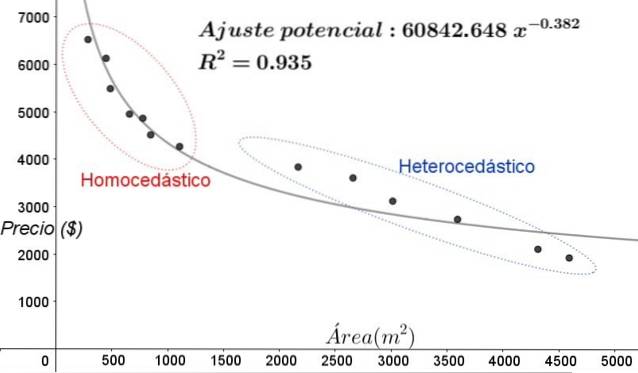
Nel grafico in Figura 5, le zone omoschedastiche ed eteroschedastiche dovrebbero essere chiaramente evidenziate. Va anche notato che queste zone sono state scambiate rispetto a quelle che si sono formate nel modello di adattamento lineare.
Nel grafico di figura 5 è evidente che anche in presenza di un coefficiente di determinazione dell'adattamento abbastanza alto (93,5%), il modello non è adeguato per l'intero intervallo della variabile esplicativa, poiché i dati per valori maggiori di 2000 m ^ 2 presente eteroschedasticità.
Uno dei test non grafici più utilizzati per verificare se l'omoschedasticità è soddisfatta o meno è il Test di Breusch-Pagan.
Non tutti i dettagli di questo test verranno forniti in questo articolo, ma le sue caratteristiche fondamentali e le fasi dello stesso sono delineate a grandi linee:
La maggior parte dei pacchetti software statistici come: SPSS, MiniTab, R, Python Pandas, SAS, StatGraphic e molti altri incorporano il test di omoscedasticità di Breusch-Pagan. Un altro test per verificare l'uniformità della varianza Test di Levene.
Nessun utente ha ancora commentato questo articolo.