Gradi di libertà come calcolarli, tipi, esempi

Il gradi di libertà in statistica sono il numero di componenti indipendenti di un vettore casuale. Se il vettore ha n componenti e ci sono p equazioni lineari che mettono in relazione le loro componenti, quindi il grado di libertà è n-p.

Il concetto di gradi di libertà Appare anche nella meccanica teorica, dove approssimativamente sono equivalenti alla dimensione dello spazio in cui si muove la particella, meno il numero di legami..

Questo articolo discuterà il concetto di gradi di libertà applicato alla statistica, ma un esempio meccanico è più facile da visualizzare in forma geometrica.

Indice articolo

• 1 Tipi di gradi di libertà
  • 1.1 In una custodia meccanica
  • 1.2 In un insieme di valori casuali
• 2 esempi
  • 2.1 Varianza e gradi di libertà
  • 2.2 Nella distribuzione del Chi quadrato
  • 2.3 Nel test di ipotesi (con l'esempio elaborato)
• 3 Riferimenti

Tipi di gradi di libertà

A seconda del contesto in cui viene applicato, il modo di calcolare il numero di gradi di libertà può variare, ma l'idea di fondo è sempre la stessa: dimensioni totali meno numero di restrizioni.

In una custodia meccanica

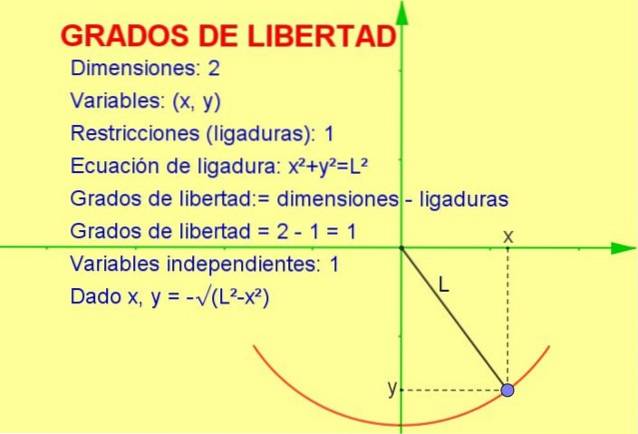
Consideriamo una particella oscillante legata ad una corda (un pendolo) che si muove nel piano verticale x-y (2 dimensioni). Tuttavia, la particella è costretta a muoversi sulla circonferenza di raggio pari alla lunghezza della corda.

Poiché la particella può muoversi solo su quella curva, il numero di gradi di libertà è 1. Questo può essere visto nella figura 1.

Il modo per calcolare il numero di gradi di libertà è prendere la differenza del numero di dimensioni meno il numero di vincoli:

gradi di libertà: = 2 (dimensioni) - 1 (legatura) = 1

Un'altra spiegazione che ci permette di arrivare al risultato è la seguente:

-Sappiamo che la posizione in due dimensioni è rappresentata da un punto di coordinate (x, y).

-Ma poiché il punto deve soddisfare l'equazione della circonferenza (x^Due + Y^Due = L^Due) per un dato valore della variabile x, la variabile y è determinata da detta equazione o restrizione.

Pertanto, solo una delle variabili è indipendente e il sistema lo ha un (1) grado di libertà.

In un insieme di valori casuali

Per illustrare il significato del concetto, supponiamo il vettore

X = (x₁, X_Due,..., X_n)

Ciò che rappresenta il campione di n valori casuali normalmente distribuiti. In questo caso il vettore casuale X avere n componenti indipendenti e quindi si dice che X avere n gradi di libertà.

Ora costruiamo il vettore r di rifiuti

r = (x₁ - , X_Due - ,…., X_n - )

Dove rappresenta la media campionaria, che viene calcolata come segue:

= (x₁ + X_Due +…. + X_n) / n

Quindi la somma

(X₁ - ) + (x_Due - ) +…. + (X_n - ) = (x₁ + X_Due +…. + X_n) - n= 0

È un'equazione che rappresenta un vincolo (o vincolo) sugli elementi del vettore r dei residui, poiché se sono noti n-1 componenti del vettore r, l'equazione del vincolo determina la componente sconosciuta.

Quindi il vettore r di dimensione n con la restrizione:

∑ (x_io - ) = 0

Avere (n - 1) gradi di libertà.

Anche in questo caso si applica che il calcolo del numero di gradi di libertà è:

gradi di libertà: = n (dimensioni) - 1 (vincoli) = n-1

Esempi

Varianza e gradi di libertà

La varianza s^Due è definita come la media del quadrato delle deviazioni (o residui) del campione di n dati:

S^Due = (r•r) / (n-1)

dove r è il vettore dei residui r = (x1 - , x2 - ,…., Xn - ) e il punto spesso (•) è l'operatore del prodotto scalare. In alternativa, la formula della varianza può essere scritta come segue:

S^Due = ∑ (x_io - )^Due / (n-1)

In ogni caso, si noti che nel calcolo della media del quadrato dei residui, viene divisa per (n-1) e non per n, poiché come discusso nella sezione precedente, il numero di gradi di libertà del vettore r è (n-1).

Se per il calcolo della varianza fossero stati divisi per n invece di (n-1), il risultato avrebbe un bias molto significativo per i valori di n sotto i 50.

In letteratura, la formula della varianza compare anche con il divisore n invece di (n-1), quando si tratta della varianza di una popolazione.

Ma l'insieme della variabile casuale dei residui, rappresentato dal vettore r, Sebbene abbia dimensione n, ha solo (n-1) gradi di libertà. Tuttavia, se il numero di dati è sufficientemente grande (n> 500), entrambe le formule convergono allo stesso risultato.

Calcolatrici e fogli di calcolo forniscono entrambe le versioni della varianza e della deviazione standard (che è la radice quadrata della varianza).

La nostra raccomandazione, in vista dell'analisi qui presentata, è di scegliere sempre la versione con (n-1) ogni volta che è necessario calcolare la varianza o la deviazione standard, per evitare risultati distorti..

Nella distribuzione del Chi quadrato

Alcune distribuzioni di probabilità in variabile casuale continua dipendono da un parametro chiamato grado di libertà, è il caso della distribuzione Chi quadrato (χ^Due).

Il nome di questo parametro deriva proprio dai gradi di libertà del sottostante vettore casuale a cui si applica questa distribuzione.

Supponiamo di avere g popolazioni, da cui vengono prelevati campioni di dimensione n:

X₁ = (x1₁, x1_Due,... X1_n)

X2 = (x2₁, x2_Due,... X2_n)

... .

X_j = (xj₁, xj_Due,... Xj_n)

... .

Xg = (xg₁, xg_Due,... Xg_n)

Una popolazione j cosa ha nella media e deviazione standard Sj, segue la distribuzione normale N (, Sj ).

La variabile standardizzata o normalizzata zj_io è definito come:

zj_io = (xj_io - ) / Sj.

E il vettore Zj è definito così:

Zj = (zj₁, zj_Due,..., zj_io,..., zj_n) e segue la distribuzione normale standardizzata N (0,1).

Quindi la variabile:

Q = ((z1₁ ^ 2 + z2₁^ 2 +…. + zg₁^ 2),…., (Z1_n^ 2 + z2_n^ 2 +…. + zg_n^ 2))

segui la distribuzione χ^Due(g) chiamato il distribuzione chi quadrato con grado di libertà g.

Nel test di ipotesi (con esempio elaborato)

Quando vuoi testare ipotesi basate su un certo insieme di dati casuali, devi conoscere il file numero di gradi di libertà g per poter applicare il test del Chi quadrato.

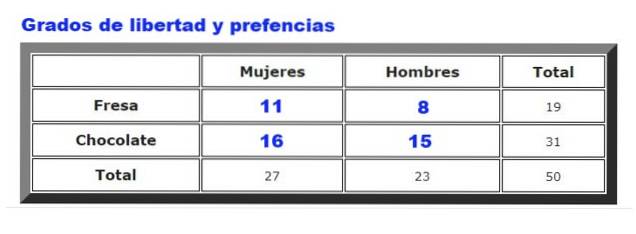
A titolo di esempio, verranno analizzati i dati raccolti sulle preferenze del gelato al cioccolato o alla fragola tra uomini e donne in una determinata gelateria. La frequenza con cui uomini e donne scelgono la fragola o il cioccolato è riassunta nella figura 2.

Innanzitutto, viene calcolata la tabella delle frequenze attese, che viene preparata moltiplicando il righe totali per lui colonne totali, diviso per dati totali. Il risultato è mostrato nella figura seguente:

Quindi procediamo a calcolare il Chi quadrato (dai dati) utilizzando la seguente formula:

χ^Due = ∑ (F_o - F_e)^Due / F_e

Dove F_o sono le frequenze osservate (Figura 2) e F_e sono le frequenze attese (Figura 3). La somma copre tutte le righe e le colonne, che nel nostro esempio danno quattro termini.

Dopo aver eseguito le operazioni ottieni:

χ^Due = 0,2043.

Ora è necessario confrontare con il Chi quadrato teorico, che dipende da numero di gradi di libertà g.

Nel nostro caso questo numero è determinato come segue:

g = (# righe - 1) (# colonne - 1) = (2-1) (2-1) = 1 * 1 = 1.

Risulta che il numero di gradi di libertà g in questo esempio è 1.

Se si vuole verificare o rifiutare l'ipotesi nulla (H0: non c'è correlazione tra GUSTO e GENERE) con un livello di significatività dell'1%, il valore Chi-quadrato teorico viene calcolato con grado di libertà g = 1.

Si cerca il valore che rende la frequenza accumulata (1 - 0,01) = 0,99, cioè 99%. Questo valore (ricavabile dalle tabelle) è 6,636.

Poiché la Chi teorica supera quella calcolata, viene verificata l'ipotesi nulla.

Cioè con i dati raccolti, Non osservato relazione tra le variabili GUSTO e GENERE.

Riferimenti

1. Minitab. Quali sono i gradi di libertà? Recupero da: support.minitab.com.
2. Moore, David. (2009) Statistiche applicate di base. Editore di Antoni Bosch.
3. Leigh, Jennifer. Come calcolare i gradi di libertà nei modelli statistici. Estratto da: geniolandia.com
4. Wikipedia. Grado di libertà (statistica). Estratto da: es.wikipedia.com
5. Wikipedia. Grado di libertà (fisico). Estratto da: es.wikipedia.com