
Valore delle funzioni trigonometriche inverse, derivate, esempi, esercizi
Il funzioni trigonometriche inverse, Come suggerisce il nome, sono le corrispondenti funzioni inverse delle funzioni seno, coseno, tangente, cotangente, secante e cosecante..
Le funzioni trigonometriche inverse sono indicate con lo stesso nome della loro corrispondente funzione trigonometrica diretta più il prefisso arco. Quindi:
1.- arcsen (x) è la funzione trigonometrica inversa della funzione sen (x)
Due.- arccos (x) è la funzione trigonometrica inversa della funzione cos (x)
3.- arctan (x) è la funzione trigonometrica inversa della funzione quindi (x)
4.- arccot (x) è la funzione trigonometrica inversa della funzione culla (x)
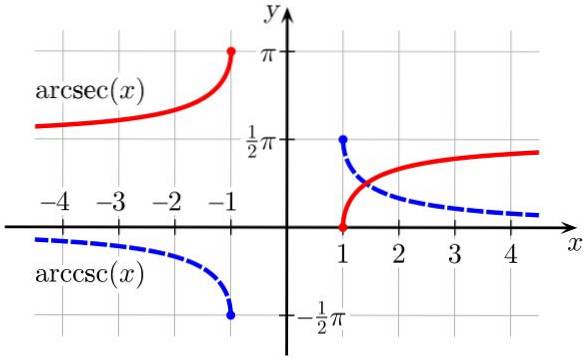
5.- arcsec (x) è la funzione trigonometrica inversa della funzione sec (x)
6.- arccsc (x) è la funzione trigonometrica inversa della funzione csc (x)
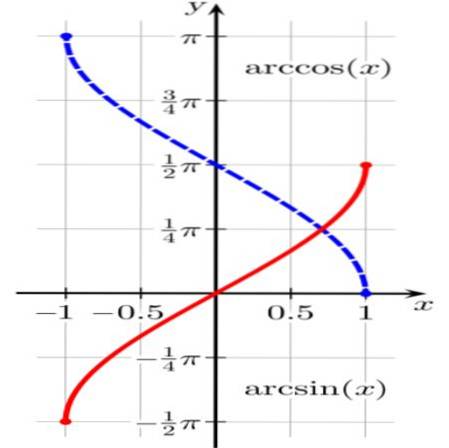
La funzione θ = arcsen (x) si traduce in un arco unitario θ (o angolo in radianti θ) tale che sin (θ) = x.
Quindi, ad esempio, arcsen (√3 / 2) = π / 3 poiché, come è noto, il seno di π / 3 radianti è uguale a √3 / 2.
Indice articolo
- 1 Valore principale delle funzioni trigonometriche inverse
- 1.1 Tabella dei domini e degli intervalli delle funzioni trigonometriche inverse
- 2 Derivate di funzioni trigonometriche inverse
- 3 esempi
- 3.1 - Esempio 1
- 3.2 - Esempio 2
- 4 esercizi
- 4.1 - Esercizio 1
- 4.2 - Esercizio 2
- 4.3 - Esercizio 3
- 5 Riferimenti
Valore principale delle funzioni trigonometriche inverse
Affinché una funzione matematica f (x) abbia un inverso g (x) = f-1(x) è necessario che questa funzione sia iniettiva, il che significa che ogni valore y dell'insieme di arrivo della funzione f (x) deriva da uno e un solo valore x.
È chiaro che questo requisito non è soddisfatto da alcuna funzione trigonometrica. Per chiarire il punto, si noti che il valore y = 0,5 può essere ottenuto dalla funzione seno nei seguenti modi:
- sin (π / 6) = 0,5
- sin (5π / 6) = 0,5
- sin (7π / 6) = 0,5
E molti altri, poiché la funzione seno è periodica con periodo 2π.
Per definire le funzioni trigonometriche inverse, è necessario restringere il dominio delle loro corrispondenti funzioni trigonometriche dirette, in modo che soddisfino il requisito di iniettività.
Quel dominio limitato della funzione diretta sarà l'intervallo o il ramo principale della sua corrispondente funzione inversa.
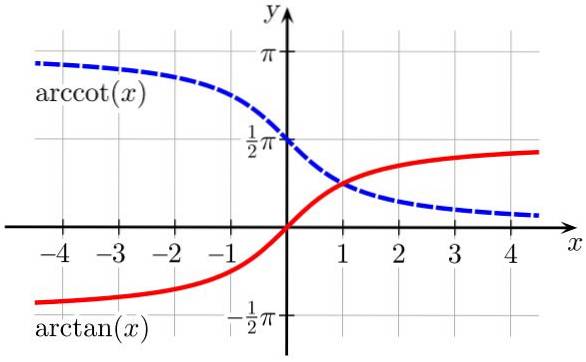
Tabella dei domini e degli intervalli delle funzioni trigonometriche inverse

Derivate di funzioni trigonometriche inverse
Per ottenere le derivate delle funzioni trigonometriche inverse si applicano le proprietà delle derivate, in particolare la derivata di una funzione inversa.
Se indichiamo con f (y) la funzione e con f-1(x) alla sua funzione inversa, quindi la derivata della funzione inversa è correlata alla derivata della funzione diretta dalla seguente relazione:
[F-1(x)] "= 1 / f" [f-1(X)]
Ad esempio: se x = f (y) = √y è la funzione diretta, il suo inverso sarà
y = f-1(x) = xDue. Applichiamo la regola della derivata dell'inverso a questo semplice caso per vedere che questa regola è effettivamente soddisfatta:
[XDue] '= 1 / [√y]' = 1 / (½ y-½ = 2 e½ = 2 (xDue)½ = 2x
Bene, possiamo usare questo trucco per trovare le derivate delle funzioni trigonometriche inverse.
Ad esempio, prendiamo θ = arcsen (x) come funzione diretta, allora la sua funzione inversa sarà sin (θ) = x.
[arcsen (x)] '= 1 / [sin (θ)]' = 1 / cos (θ) = 1 / √ (1 - sin (θ)Due) = ...
… = 1 / √ (1 - xDue) .
In questo modo si possono ottenere tutte le derivate delle funzioni trigonometriche inverse, che vengono mostrate di seguito:

Queste derivate sono valide per qualsiasi argomento z appartenente ai numeri complessi e quindi sono valide anche per qualsiasi argomento reale x, poiché z = x + 0i.
Esempi
- Esempio 1
Trova arctan (1).
Soluzione
L'arctan (1) è l'arco unitario (angolo in radianti) ፀ tale che tan (ፀ) = 1. Quell'angolo è ፀ = π / 4 perché tan (π / 4) = 1. Quindi arctan (1) = π / 4.
- Esempio 2
Calcola arcsen (cos (π / 3)).
Soluzione
L'angolo π / 3 radianti è un angolo notevole il cui coseno è ½, quindi il problema si riduce a trovare arcsen (½).
Quindi si tratta di trovare qual è l'angolo il cui seno dà ½. Quell'angolo è π / 6, poiché sin (π / 6) = sin (30º) = ½. Quindi arcsen (cos (π / 3)) = π / 6.
Formazione
- Esercizio 1
Trova il risultato della seguente espressione:
sec (arctan (3)) + csc (arccot (4))
Soluzione
Iniziamo nominando α = arctan (3) e β = arccot (4). Quindi l'espressione che dobbiamo calcolare è simile a questa:
sec (α) + csc (β)
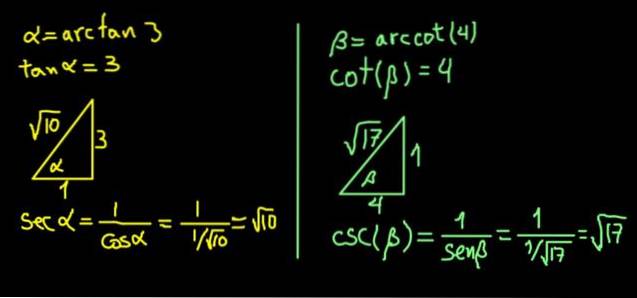
L'espressione α = arctan (3) equivale a dire tan (α) = 3.
Poiché la tangente è la gamba opposta su quella adiacente, costruiamo un triangolo rettangolo con la gamba opposta α di 3 unità e una gamba adiacente di 1 unità, in modo che tan (α) = 3/1 = 3.
In un triangolo rettangolo l'ipotenusa è determinata dal teorema di Pitagora. Con questi valori il risultato è √10, quindi:
sec (α) = ipotenusa / gamba adiacente = √10 / 1 = √10.
Allo stesso modo β = arccot (4) equivale ad affermare che cot (β) = 4.
Costruiamo un triangolo della gamba destra adiacente a β di 4 unità e una gamba opposta di 1 unità, in modo che cot (β) = 4/1.
Il triangolo si completa immediatamente trovando la sua ipotenusa grazie al teorema di Pitagora. In questo caso si è scoperto che aveva √17 unità. Quindi viene calcolato il csc (β) = ipotenusa / gamba opposta = √17 / 1 = √17.
Ricordando che l'espressione che dobbiamo calcolare è:
sec (arctan (3)) + csc (arccot (4)) = sec (α) + csc (β) =…
… = √10 + √17 = 3,16 + 4,12 = 7,28.
- Esercizio 2
Trova le soluzioni di:
Cos (2x) = 1 - Sen (x)

Soluzione
È necessario che tutte le funzioni trigonometriche siano espresse nello stesso argomento o angolo. Useremo l'identità del doppio angolo:
Cos (2x) = 1 - 2 SenDue(X)
Quindi l'espressione originale è ridotta a:
1 - 2 SenDue(x) = 1 - Sen x
Una volta semplificato e scomposto, si esprime come:
sin (x) (2 sin (x) - 1) = 0
Il che dà origine a due possibili equazioni: Sen (x) = 0 con soluzione x = 0 e un'altra equazione sin (x) = ½ con x = π / 6 come soluzione.
Le soluzioni dell'equazione sono: x = 0 o x = π / 6.
- Esercizio 3
Trova le soluzioni della seguente equazione trigonometrica:
cos (x) = sinDue(X)
Soluzione
Per risolvere questa equazione è conveniente posizionare un solo tipo di funzione trigonometrica, quindi useremo l'identità trigonometrica fondamentale in modo che l'equazione originale venga riscritta come segue:
cos (x) = 1 - cosDue(X)
Se chiamiamo y = cos (x), l'espressione può essere riscritta come:
YDue + e - 1 = 0
È un'equazione di secondo grado in y, le cui soluzioni sono:
y = (-1 ± √5) / 2
Quindi i valori di x che soddisfano l'equazione originale sono:
x = arccos ((-1 ± √5) / 2)
La soluzione reale è quella con segno positivo x = 0,9046 rad = 51,83º.
L'altra soluzione è complessa: x = (π - 1.06 i) rad.
Riferimenti
- Hazewinkel, M. 1994. Encyclopaedia of Mathematics. Kluwer Academic Publishers / Springer Science & Business Media.
- Mate Mobile. Funzioni trigonometriche inverse. Estratto da: matemovil.com
- Formule dell'universo. Funzioni trigonometriche inverse. Estratto da: universoformulas.com
- Weisstein, Eric W. Funzioni trigonometriche inverse. Estratto da: mathworld.wolfram.com
- Wikipedia. Funzioni trigonometriche inverse. Estratto da: en.wikipedia.com


Nessun utente ha ancora commentato questo articolo.