
Funzioni trigonometriche di base, nel piano cartesiano, esempi, esercizio
Il funzioni trigonometriche di variabile reale corrispondono a qualsiasi angolo (espresso in radianti), un rapporto trigonometrico, che può essere seno, coseno, tangente, cotangente, secante e cosecante.
In questo modo abbiamo le sei funzioni trigonometriche: seno, coseno, tangente, cosecante, secante e cotangente..
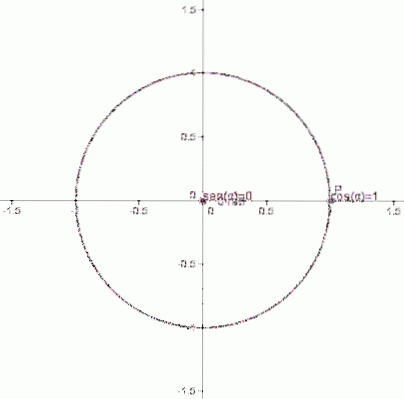
Le funzioni trigonometriche per angoli compresi tra 0 e 2π si definiscono con l'ausilio della circonferenza unitaria, di raggio 1 e il cui centro coincide con quello di origine del sistema di coordinate cartesiane: il punto (0,0).
Possiamo individuare qualsiasi punto P di coordinate (x, y) su questa circonferenza.
Il segmento che unisce l'origine con P, insieme ai rispettivi segmenti che uniscono le proiezioni di P sugli assi coordinati, formano un triangolo rettangolo, i cui rapporti trigonometrici sono noti come rapporti tra i lati del triangolo. A) Sì:
- sin θ = gamba opposta / ipotenusa
- cos θ = gamba adiacente / ipotenusa
- tg θ = gamba opposta / gamba adiacente
E ora i motivi che sono il contrario dei precedenti:
- sec θ = ipotenusa / gamba adiacente
- cosec θ = ipotenusa / gamba opposta
- ctg θ = gamba adiacente / gamba opposta
Nel cerchio unitario l'ipotenusa di qualsiasi triangolo è uguale a 1 e le gambe valgono xey, quindi:
sin θ = y
cos θ = x
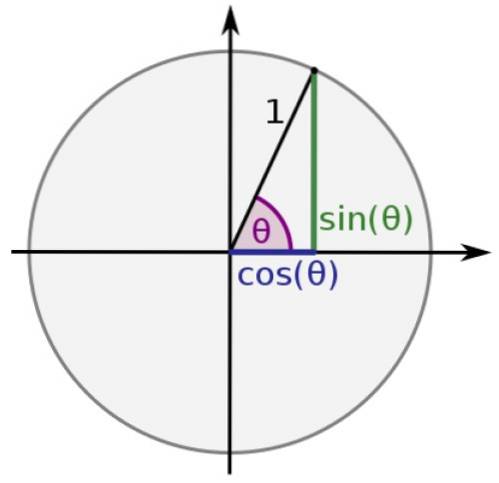
In questo modo le funzioni seno e coseno acquisiscono sempre valori compresi tra -1 e 1, mentre il resto:
tg θ = y / x
cosec θ = 1 / y
sec θ = 1 / x
Non sono definiti quando X o Y vale 0.
Indice articolo
- 1 Funzioni trigonometriche nel piano cartesiano
- 1.1 Funzione f (x) = sin x
- 1.2 Funzione f (x) = cos x
- 1.3 Funzioni trigonometriche discontinue
- 2 Esercizio risolto
- 2.1 Soluzione
- 3 Riferimenti
Funzioni trigonometriche sul piano cartesiano
Come vedremo di seguito, le funzioni trigonometriche sono caratterizzate dall'essere periodiche. Pertanto, non sono biiettivi, tranne che in un dominio limitato..
Funzione f (x) = sin x
Partendo dal cerchio trigonometrico nel punto P (1,0), l'angolo è 0 radianti. Quindi il raggio ruota in senso antiorario e la funzione sin x cresce gradualmente fino a raggiungere π / 2 radianti (90º), equivalenti a circa 1.571 radianti..
Qui raggiunge il valore y = 1 e poi diminuisce fino a raggiungere lo zero in π radianti (180 °). Successivamente diminuisce ancora di più, poiché il valore diventa negativo fino a raggiungere −1 quando l'angolo è 3π / 2 radianti (270 °).
Infine, aumenta di nuovo fino a tornare a zero a 360 °, dove tutto ricomincia. Questo rende y = sin x a funzione periodica di periodo 2π, quindi la funzione seno non è biiettiva.
Inoltre, il grafico è simmetrico rispetto al punto (0,0), quindi la funzione è dispari.
Quindi il grafico di y = sin x:
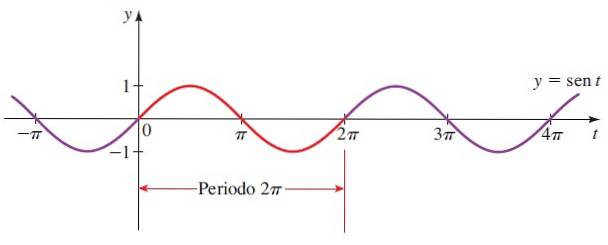
La sezione in rosso è il primo periodo. Vengono considerati anche gli angoli negativi, poiché il raggio del cerchio trigonometrico può ruotare in senso orario.
Dominio del peccato x = Tutti reali.
Gamma o percorso del peccato x = [-1,1]
Funzione f (x) = cos x
Nel punto P (1,0) la funzione coseno vale 1 e da lì decresce, arrivando a 0 quando l'angolo è π / 2. Continua a diminuire e assume valori negativi, fino a raggiungere -1 all'angolo π.
Quindi inizia ad aumentare gradualmente fino a raggiungere 0 in 3π / 2 e torna al valore 1 quando il raggio ha compiuto un giro completo. Da lì il ciclo si ripete, poiché cos x è periodico ed è anche uniforme (simmetrico attorno all'asse verticale).
La forma della funzione coseno è la stessa di quella della funzione seno, tranne per il fatto che sono spostati π / 2 l'uno rispetto all'altro..
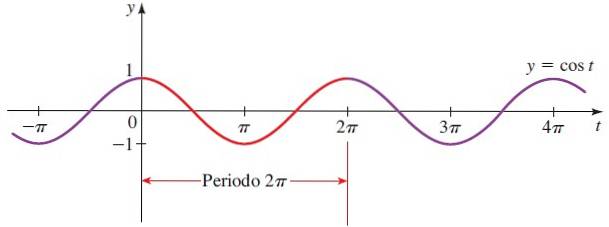
Dominio di cos x = Tutti reali.
Cos x gamma o viaggio = [-1,1]
Funzioni trigonometriche discontinue
Le funzioni tg x, ctg x, sec x e cosec x sono discontinue, poiché sono quozienti tra seno e coseno, o l'inverso. Poiché questi valgono 0 in alcuni angoli, quando compaiono al denominatore rendono discontinua la funzione.
E poiché seno e coseno sono funzioni periodiche, anche le funzioni tg x, ctg x, sec x, cosec x sono periodiche..
Funzione tangente f (x) = tg x
Per la funzione tangente, i valori di discontinuità sono: ± π / 2, ± 3π / 2, ± 5π / 2… La funzione assume valori molto grandi o molto piccoli. In generale, questo accade per tutti i multipli di π della forma (2n + 1) π / 2, sia positivi che negativi, con n = 0, 1, 2 ...
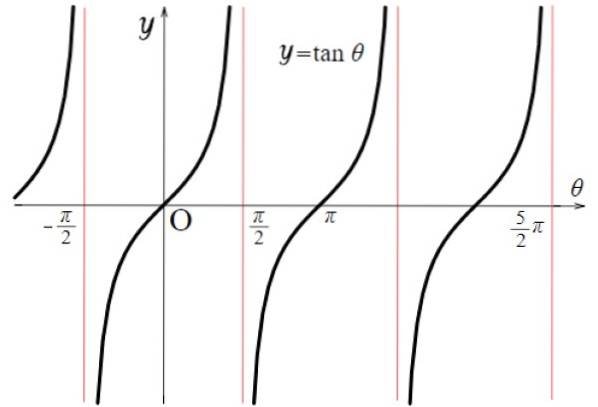
Perciò:
Dominio tg x: D = x ∈ R / x ≠ (2n + 1) π / 2; n ∈ Z
Tg x portata o viaggio: Tutto vero.
Si noti che la funzione f (x) = tg x si ripete tra - π / 2 e + π / 2, quindi il suo periodo è π. Inoltre, è simmetrico rispetto all'origine.
Funzione cotangente f (x) = ctg x
Per questa funzione i valori di discontinuità si verificano a 0, ± π, ± 2π…, cioè i multipli interi di π.
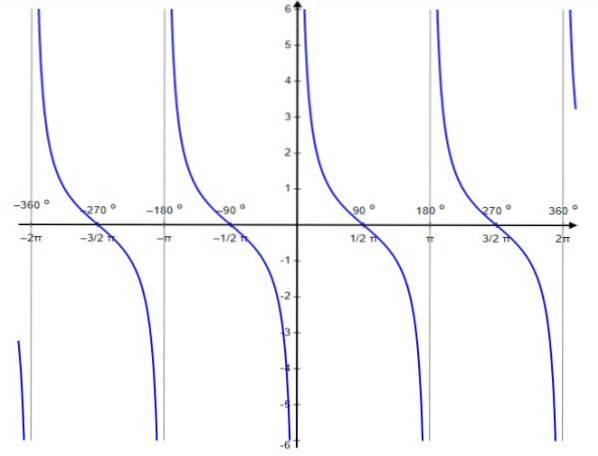
Come la funzione tangente, la funzione cotangente è periodica del periodo π. Per lei è vero che:
Dominio ctg x: D = x ∈ R / x ≠ n π; n ∈ Z
Ctg x range o travel: Tutto vero.
Funzione secante f (x) = sec x
La funzione sec x ha punti di discontinuità a ± π / 2, ± 3π / 2, ± 5π / 2…, dove cos x = 0. È anche periodica con periodo π ed è anche osservato dal grafico che la funzione non assume mai valori nell'intervallo (-1,1)
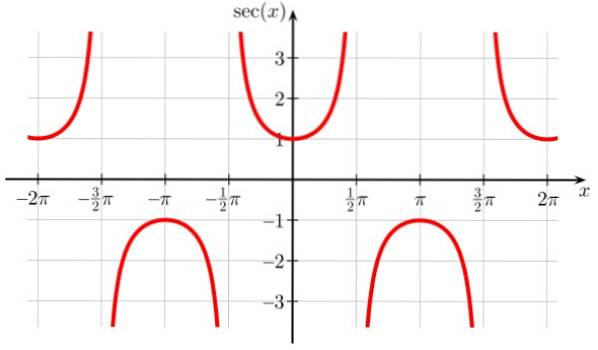
Dominio di sec x: D = x ∈ R / x ≠ (2n + 1) π / 2; n ∈ Z
Sec x portata o corsa: Tutti i reali tranne (-1,1)
Funzione cosecante f (x) = cosec x
È simile alla funzione secante, sebbene sia spostata a destra, quindi i punti di discontinuità sono 0, ± π, ± 2π e tutti i multipli interi di π. È anche periodico.
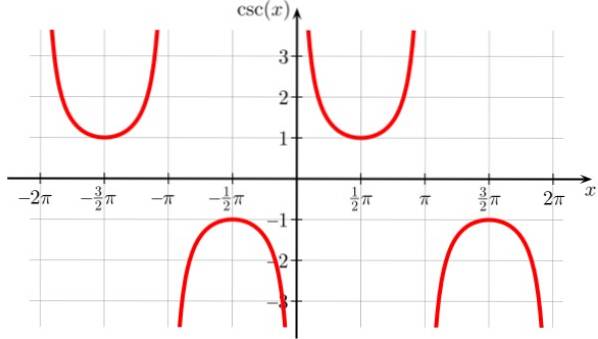
Cosec Domain X: D = x ∈ R / x ≠ n π; n ∈ Z
Area di raccolta o percorso x: Tutti i reali tranne (-1,1)
Esercizio risolto
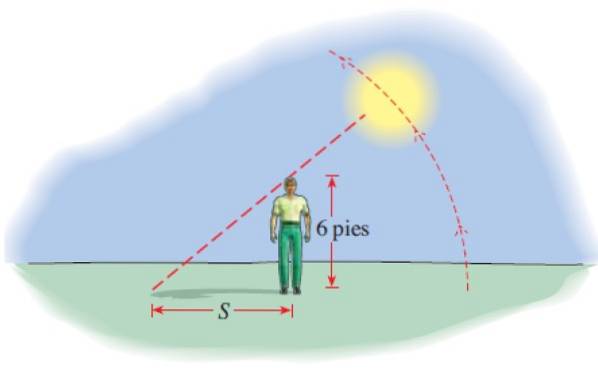
Un uomo alto 6 piedi proietta un'ombra S la cui lunghezza è data da:
S (t) = 6 │cot (π.t / 12) │
Con S in piedi et il numero di ore trascorse dalle 6 del mattino. Quanto è alta l'ombra alle 8:00, 12:00, 14:00 e 17:45?
Soluzione
Dobbiamo valutare la funzione per ciascuno dei valori dati, nota che deve assumere il valore assoluto, poiché la lunghezza dell'ombra è positiva:
-Alle 8 del mattino sono trascorse 2 ore dalle 6 del mattino, quindi t = 2 e S (t) è:
S (2) = 6 │cot (π.2 / 12) │ft = 6 │cot (π / 6) │ft = 10,39 piedi.
-Quando è 12 N, sono trascorse t = 6 ore, quindi:
S (6) = 6 │cot (π.6 / 12) │ft = 6 │cot (π / 2) │ft = 0 piedi. (In quel momento il Sole cade verticalmente sulla testa della persona).
-Alle 14:00 t = 8 ore trascorse:
S (8) = 6 │cot (π.8 / 12) │ft = 6 │cot (2π / 3) │ft = 3,46 piedi.
-Quando sono le 17:45, sono già trascorse 11,75 ore dalle 6 del mattino, quindi:
S (11,75) = 6 │cotto (π x 11,75 / 12) │ piedi = 91,54 piedi. A quest'ora le ombre si allungano.
Il lettore può calcolare il tempo in cui l'ombra della persona è uguale alla sua altezza??
Riferimenti
- Carena, M. 2019. Manuale di matematica pre-universitaria. Università Nazionale del Litorale.
- Figuera, J. 1999. Matematica. 1 °. Diversificato. Bolivarian Collegiate Editions.
- Hoffman, J. Selezione di argomenti di matematica. Volume 4.
- Jiménez, R. 2008. Algebra. Prentice Hall.
- Zill, D. 1984. Algebra e trigonometria. Mcgraw hill.


Nessun utente ha ancora commentato questo articolo.