
Definizione di funzione surrogata, proprietà, esempi
UN funzione suriettiva è qualsiasi relazione in cui ogni elemento appartenente al codominio è un'immagine di almeno un elemento del dominio. Conosciuta anche come funzione sopra, fanno parte della classificazione delle funzioni rispetto al modo in cui i loro elementi sono correlati.
Ad esempio una funzione FA → B definito da F (x) = 2x
Che legge "F che dire PER fino a B definito da F (x) = 2x "
È il momento di definire i set di partenza e di arrivo A e B.
A: 1, 2, 3, 4, 5 Ora i valori o le immagini che ciascuno di questi elementi mostrerà quando valutato in F, saranno gli elementi del codominio.
F (1) = 2
F (2) = 4
F (3) = 6
F (4) = 8
F (5) = 10
Formando così il tutto B: 2, 4, 6, 8, 10
Si può quindi concludere che:
F: 1, 2, 3, 4, 5 → 2, 4, 6, 8, 10 definito da F (x) = 2x È una funzione suriettiva
Ogni elemento del codominio deve risultare da almeno un'operazione della variabile indipendente attraverso la funzione in questione. Non c'è limitazione di immagini, un elemento del codominio può essere un'immagine di più di un elemento del dominio e ancora provandone uno funzione suriettiva.
L'immagine mostra 2 esempi con funzioni suriettive.
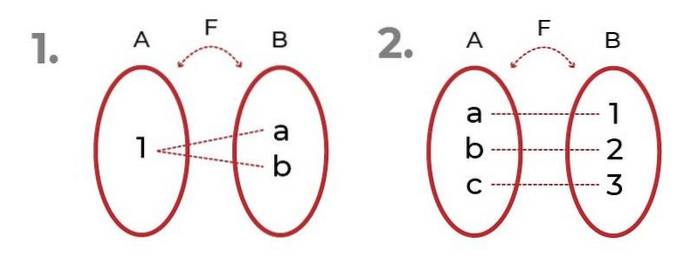
Nella prima si osserva che le immagini possono essere riferite allo stesso elemento, senza compromettere il suriettività della funzione.
Nella seconda vediamo un'equa distribuzione tra dominio e immagini. Questo dà luogo a funzione biiettiva, dove i criteri di funzione iniettiva e funzione suriettiva.
Un altro metodo di identificazione funzioni suriettive, è controllare se il codominio è uguale all'intervallo della funzione. Ciò significa che se il set di arrivo è uguale alle immagini fornite dalla funzione in fase di valutazione della variabile indipendente, la funzione è suriettiva.
Indice articolo
- 1 Proprietà
- 1.1 Condizionamento funzionale
- 2 Esempi: esercizi risolti
- 2.1 Esercizio 1
- 2.2 Esercizio 2
- 2.3 Esercizio 3
- 2.4 Esercizio 4
- 2.5 Esercizio 4
- 2.6 Esercizio 5
- 3 Esercizi proposti
- 4 Riferimenti
Proprietà
Considerare surjective per una funzione deve essere soddisfatto quanto segue:
Essere F: DF → CF
∀ b ℮ CF E a ℮ DF / F (a) = b
Questo è il modo algebrico per stabilirlo per ogni "b" che appartiene a CF c'è una "a" che appartiene a DF tale che la funzione F valutata in "a" sia uguale a "b".
La suriettività è una peculiarità delle funzioni, dove il codominio e la gamma sono simili. Pertanto, gli elementi valutati nella funzione costituiscono l'insieme di arrivo.
Condizionamento funzionale
A volte una funzione che non lo è surjective, può essere soggetto a determinate condizioni. Queste nuove condizioni possono renderlo un file funzione suriettiva.
Sono validi tutti i tipi di modifiche al dominio e al codominio della funzione, dove l'obiettivo è soddisfare le proprietà di suriettività nella relazione corrispondente.
Esempi: esercizi risolti
Per soddisfare le condizioni di suriettività devono essere applicate diverse tecniche di condizionamento, questo al fine di garantire che ogni elemento del codominio rientri nel set di immagini della funzione.
Esercizio 1
- Lascia che la funzione F: R → R definito dalla linea F (x) = 8 - x
A: [Tutti i numeri reali]
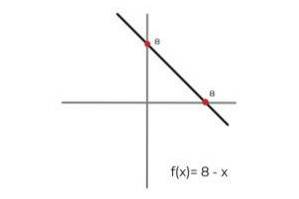
In questo caso, la funzione descrive una linea continua, che copre tutti i numeri reali sia nel suo dominio che nel suo intervallo. Perché la gamma della funzione RF è uguale a codominio R Si può concludere che:
F: R → R definito dalla linea F (x) = 8 - x è un funzione suriettiva.
Questo vale per tutte le funzioni lineari (funzioni il cui massimo grado di variabile è uno).
Esercizio 2
- Studia la funzione F: R → R definito da F (x) = xDue : Definisci se è un file funzione suriettiva. In caso contrario, mostra le condizioni necessarie per renderlo surrogativo.
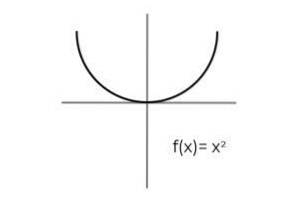
La prima cosa da considerare è il codominio di F, che si compone dei numeri reali R. Non c'è modo per la funzione di restituire valori negativi, il che esclude i veri negativi dalle possibili immagini.
Condizionamento del codominio all'intervallo [0 , ∞ ]. Si evita di lasciare elementi del codominio non correlati F.
Le immagini vengono ripetute per coppie di elementi della variabile indipendente, come x = 1 Y x = - 1. Ma questo riguarda solo il file iniettività della funzione, non essendo un problema per questo studio.
In questo modo si può concludere che:
F: R →[0, ∞ ) definito da F (x) = xDue È una funzione suriettiva
Esercizio 3
- Definisci le condizioni del codominio che avrebbero fatto suriettivi alle funzioni
F: R → R definito da F (x) = Sen (x)
F: R → R definito da F (x) = Cos (x)
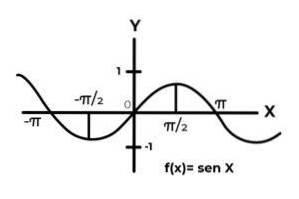
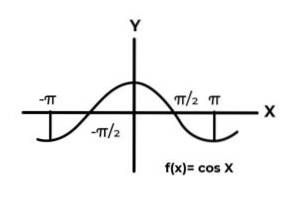
Il comportamento delle funzioni trigonometriche è simile a quello delle onde, essendo molto comune trovare ripetizioni della variabile dipendente tra le immagini. Anche nella maggior parte dei casi il raggio della funzione è limitato a uno o più settori della linea reale.
Questo è il caso delle funzioni seno e coseno. Dove i loro valori fluttuano nell'intervallo [-1, 1]. Questo intervallo deve condizionare il codominio al raggiungimento della suriettività della funzione.
F: R →[ -undici ] definito da F (x) = Sen (x) È una funzione suriettiva
F: R →[ -undici ]definito da F (x) = Cos (x) È una funzione suriettiva
Esercizio 4
- Studia la funzione
F: [0, ∞ ) → R definito da F (x) = ± √x denota se è un funzione suriettiva
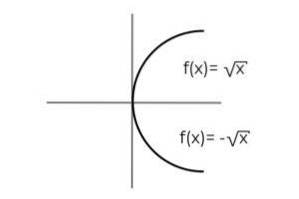
La funzione F (x) = ± √x Ha la particolarità di definire 2 variabili dipendenti per ogni valore di "x". In altre parole, l'intervallo riceve 2 elementi per ciascuno creato nel dominio. È necessario verificare un valore positivo e uno negativo per ogni valore di "x".
Osservando l'insieme di partenza, si nota che il dominio è già stato ristretto, questo per evitare le indeterminatezze prodotte nella valutazione di un numero negativo all'interno di una radice pari.
Quando si verifica l'intervallo della funzione, si nota che ogni valore del codominio appartiene all'intervallo.
In questo modo si può concludere che:
F: [0, ∞ ) → R definito da F (x) = ± √x È una funzione suriettiva
Esercizio 4
- Studia la funzione F (x) = Ln x denota se è un funzione suriettiva. Condizionare i set di arrivo e partenza per adattare la funzione ai criteri di suriettività.
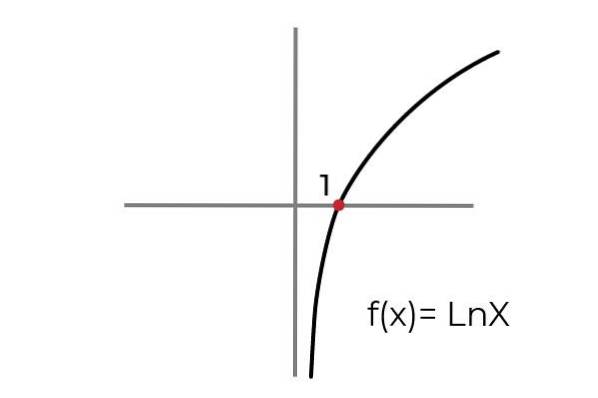
Come mostrato nel grafico la funzione F (x) = Ln xè definito per valori di "x" maggiori di zero. Mentre i valori di "e" o le immagini possono assumere qualsiasi valore reale.
In questo modo possiamo limitare il dominio di F (x) = all'intervallo (0 , ∞ )
Finché l'intervallo della funzione può essere mantenuto come l'insieme dei numeri reali R.
Considerando ciò, si può concludere che:
F: [0, ∞ ) → R definito da F (x) = Ln x È una funzione suriettiva
Esercizio 5
- Studia la funzione del valore assoluto F (x) = | x | e designare i set di arrivo e di partenza che soddisfano i criteri di suriettività.
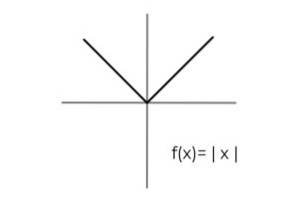
Il dominio della funzione vale per tutti i numeri reali R. In questo modo, l'unico condizionamento deve essere effettuato nel codominio, tenendo conto che la funzione valore assoluto assume solo valori positivi..
Si procede a stabilire il codominio della funzione equiparandolo al rango della stessa
[0 , ∞ )
Ora si può concludere che:
F: [0, ∞ ) → R definito da F (x) = | x | È una funzione suriettiva
Esercizi proposti
- Controlla se le seguenti funzioni sono suriettive:
- F: (0, ∞ ) → R definito da F (x) = Log (x + 1)
- F: R → R definito da F (x) = x3
- F: R →[1, ∞ ) definito da F (x) = xDue + 1
- [0, ∞ ) → R definito da F (x) = Log (2x + 3)
- F: R → R definito da F (x) = Sec x
- F: R - 0 → R definito da F (x) = 1 / x
Riferimenti
- Introduzione alla logica e al pensiero critico. Merrilee H. Salmon. Università di Pittsburgh
- Problemi nell'analisi matematica. Piotr Biler, Alfred Witkowski. Università di Wroclaw. Polonia.
- Elementi di analisi astratta. Mícheál O'Searcoid PhD. Dipartimento di matematica. College universitario di Dublino, Beldfield, Dublino 4
- Introduzione alla logica e alla metodologia delle scienze deduttive. Alfred Tarski, New York Oxford. La stampa dell'università di Oxford.
- Principi di analisi matematica. Enrique Linés Escardó. Editoriale Reverté S. A 1991. Barcellona Spagna.



Nessun utente ha ancora commentato questo articolo.