Il frequenza cumulativa è la somma delle frequenze assolute f, dalla più bassa a quella che corrisponde ad un certo valore della variabile. A sua volta, la frequenza assoluta è il numero di volte in cui un'osservazione appare nel set di dati.
Ovviamente, la variabile di studio deve essere ordinabile. E poiché la frequenza accumulata si ottiene sommando le frequenze assolute, risulta che la frequenza accumulata fino all'ultimo dato, deve coincidere con il totale di esse. Altrimenti c'è un errore nei calcoli.
Di solito la frequenza cumulativa è indicata come Fio (o talvolta nio), per distinguerla dalla frequenza assoluta fio ed è importante aggiungere una colonna per esso nella tabella con cui sono organizzati i dati, nota come tabella delle frequenze.
Ciò rende più facile, tra le altre cose, tenere traccia di quanti dati sono stati conteggiati per una determinata osservazione..
A Fio è anche conosciuto come frequenza cumulativa assoluta. Se diviso per i dati totali, abbiamo il frequenza cumulativa relativa, la cui somma finale deve essere uguale a 1.
Indice articolo
La frequenza cumulativa di un dato valore della variabile Xio è la somma delle frequenze assolute f di tutti i valori minori o uguali ad essa:
Fio = f1 + FDue + F3 +... fio
Sommando tutte le frequenze assolute si ottiene il numero totale di dati N, ovvero:
F1 + FDue + F3 +…. + Fn = N
L'operazione precedente è scritta in modo sintetico per mezzo del simbolo di sommatoria:
∑ Fio = N
Si possono anche accumulare le seguenti frequenze:
-Frequenza relativa: si ottiene dividendo la frequenza assoluta fio tra i dati totali N:
Fr = fio / N
Se si sommano le frequenze relative dalla più bassa a quella corrispondente a una certa osservazione, si ha il frequenza relativa cumulativa. L'ultimo valore deve essere uguale a 1.
-Frequenza relativa cumulativa percentuale: la frequenza relativa accumulata viene moltiplicata per 100%.
F% = (fio / N) x 100%
Queste frequenze sono utili per descrivere il comportamento dei dati, ad esempio quando si trovano le misure di tendenza centrale.
Per ottenere la frequenza accumulata, è necessario ordinare i dati e organizzarli in una tabella delle frequenze. La procedura è illustrata nella seguente situazione pratica:
-In un negozio online che vende telefoni cellulari, il record di vendite di un determinato marchio per il mese di marzo ha mostrato i seguenti valori giornalieri:
1; Due; 1; 3; 0; 1; 0; Due; 4; Due; 1; 0; 3; 3; 0; 1; Due; 4; 1; Due; 3; Due; 3; 1; Due; 4; Due; 1; 5; 5; 3
La variabile è la numero di telefoni venduti al giorno ed è quantitativa. I dati presentati in questo modo non sono così facili da interpretare, ad esempio i proprietari del negozio potrebbero essere interessati a sapere se c'è qualche tendenza, come i giorni della settimana in cui le vendite di quel marchio sono più alte..
Informazioni come questa e altre possono essere ottenute presentando i dati in modo ordinato e specificando le frequenze..
Per calcolare la frequenza cumulativa, i dati vengono prima ordinati:
0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; Due; Due; Due; Due; Due; Due; Due; Due; 3; 3; 3; 3; 3; 3; 4; 4; 4; 5; 5
Quindi viene creata una tabella con le seguenti informazioni:
-La prima colonna a sinistra con il numero di telefoni venduti, compreso tra 0 e 5 e in ordine crescente.
-Seconda colonna: frequenza assoluta, ovvero il numero di giorni in cui sono stati venduti 0 telefoni, 1 telefono, 2 telefoni e così via.
-Terza colonna: la frequenza accumulata, costituita dalla somma della frequenza precedente più la frequenza dei dati da considerare.
Questa colonna inizia con i primi dati nella colonna della frequenza assoluta, in questo caso è 0. Per il valore successivo, aggiungilo al precedente. Continua così fino a raggiungere l'ultimo dato della frequenza accumulata, che deve coincidere con il dato totale.
La tabella seguente mostra la variabile "numero di telefoni venduti in un giorno", la sua frequenza assoluta e il calcolo dettagliato della sua frequenza accumulata.
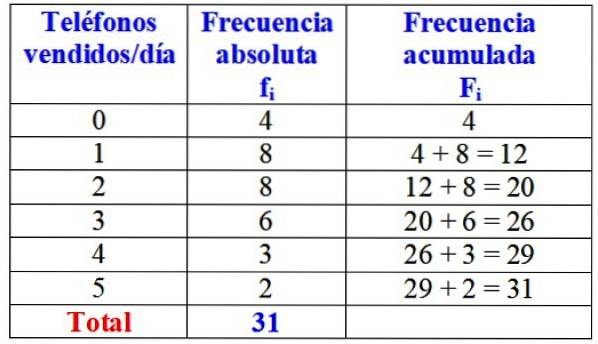
A prima vista, si potrebbe affermare che del brand in questione, uno o due telefoni vengono venduti quasi sempre al giorno, poiché la frequenza assoluta più alta è di 8 giorni, che corrisponde a questi valori della variabile. Solo durante 4 giorni del mese non hanno venduto un solo telefono.
Come notato, la tabella è più facile da esaminare rispetto ai dati individuali originariamente raccolti.
Una distribuzione di frequenza cumulativa è una tabella che mostra le frequenze assolute, le frequenze cumulative, le frequenze relative cumulative e le frequenze percentuali cumulative..
Sebbene vi sia il vantaggio di organizzare i dati in una tabella come la precedente, se il numero di dati è molto grande, potrebbe non essere sufficiente organizzarli come mostrato sopra, perché se ci sono molte frequenze diventa ancora difficile interpretare.
Il problema può essere risolto costruendo un file distribuzione di frequenza per intervalli, una procedura utile quando la variabile assume un numero elevato di valori o se è una variabile continua.
Qui i valori sono raggruppati in intervalli di uguale ampiezza, chiamati classe. Le classi sono caratterizzate dall'avere:
-Limite di classe: sono i valori estremi di ogni intervallo, ce ne sono due, il limite superiore e il limite inferiore. In generale, il limite superiore non appartiene all'intervallo ma a quello successivo, mentre il limite inferiore appartiene.
-Voto di classe: è il punto medio di ogni intervallo e viene preso come valore rappresentativo di esso.
-Larghezza classe: Viene calcolato sottraendo il valore dei dati più grandi e più piccoli (intervallo) e dividendo per il numero di classi:
Larghezza classe = intervallo / numero di classi
L'elaborazione della distribuzione delle frequenze è dettagliata di seguito..
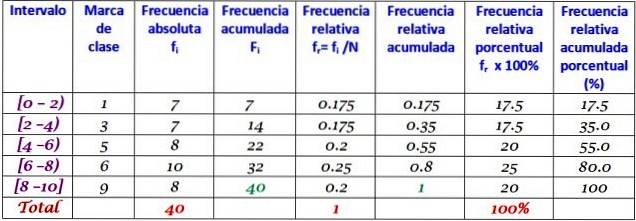
Questo set di dati corrisponde a 40 punti di un test di matematica, su una scala da 0 a 10:
0; 0; 0; 1; 1; 1; 1; Due; Due; Due; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 9; 9; 10; 10.
È possibile effettuare una distribuzione di frequenza con un certo numero di classi, ad esempio 5 classi. Va tenuto presente che quando si utilizzano molte classi, i dati non sono di facile interpretazione e si perde il senso di eseguire il raggruppamento.
E se, al contrario, sono raggruppati in pochissimi, l'informazione viene diluita e parte di essa viene persa. Tutto dipende dalla quantità di dati che hai.
In questo esempio, è una buona idea avere due punteggi in ogni intervallo, poiché ci sono 10 punteggi e verranno create 5 classi. L'intervallo è la sottrazione tra il voto più alto e quello più basso, l'ampiezza della classe è:
Larghezza classe = (10-0) / 5 = 2
Gli intervalli sono chiusi a sinistra e aperti a destra (tranne l'ultimo), che è simboleggiato rispettivamente da parentesi e parentesi. Hanno tutti la stessa larghezza, ma non è obbligatorio, sebbene lo sia più spesso.
Ogni intervallo contiene una certa quantità di elementi o una frequenza assoluta e nella colonna successiva è la frequenza accumulata, in cui viene trasportata la somma. La tabella mostra anche la frequenza relativa fr (frequenza assoluta tra il numero totale di dati) e la frequenza relativa percentuale fr × 100%.
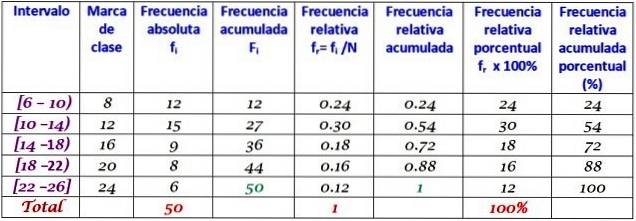
Un'azienda ha chiamato quotidianamente i propri clienti durante i primi due mesi dell'anno. I dati sono i seguenti:
6, 12, 7, 15, 13, 18, 20, 25, 12, 10, 8, 13, 15, 6, 9, 18, 20, 24, 12, 7, 10, 11, 13, 9, 12, 15, 18, 20, 13, 17, 23, 25, 14, 18, 6, 14, 16, 9, 6, 10, 12, 20, 13, 17, 14, 26, 7, 12, 24, 7
Raggruppa in 5 classi e costruisci la tabella con la distribuzione delle frequenze.
La larghezza della classe è:
(26-6) / 5 = 4
Prova a capirlo prima di vedere la risposta.
Nessun utente ha ancora commentato questo articolo.