
Formula di frequenza assoluta, calcolo, distribuzione, esempio
Il Assoluta frequenza È definito come il numero di volte in cui lo stesso dato viene ripetuto all'interno dell'insieme di osservazioni di una variabile numerica. La somma di tutte le frequenze assolute equivale al totale dei dati.
Quando si hanno molti valori di una variabile statistica, è conveniente organizzarli in modo appropriato per estrarre informazioni sul suo comportamento. Tali informazioni sono date dalle misure di tendenza centrale e dalle misure di dispersione..
Nei calcoli di queste misure, i dati sono rappresentati attraverso la frequenza con cui compaiono in tutte le osservazioni..
Il seguente esempio mostra quanto sia rivelatrice la frequenza assoluta di ogni dato. Durante la prima metà di maggio, queste sono state le taglie di abiti da cocktail più vendute da un noto negozio di abbigliamento femminile:
8; 10; 8; 4; 6; 10; 12; 14; 12; 16; 8; 10; 10; 12; 6; 6; 4; 8; 12; 12; 14; 16; 18; 12; 14; 6; 4; 10; 10; 18
Quanti vestiti vengono venduti in una particolare taglia, ad esempio la taglia 10? I proprietari sono interessati a sapere per ordinare.
Ordinare i dati rende più facile il conteggio, ci sono esattamente 30 osservazioni in totale, che ordinate dalla dimensione più piccola alla più grande sono le seguenti:
4; 4; 4; 6; 6; 6; 6; 8; 8; 8; 8; 10; 10; 10; 10; 10; 10; 12; 12; 12; 12; 12; 12; 14; 14; 14; 16; 16; 18; 18
E ora è evidente che la dimensione 10 viene ripetuta 6 volte, quindi la sua frequenza assoluta è uguale a 6. La stessa procedura viene eseguita per trovare la frequenza assoluta delle rimanenti dimensioni..
Indice articolo
- 1 Formule
- 1.1 Altre frequenze
- 2 Come ottenere la frequenza assoluta?
- 2.1 Tabulazione
- 2.2 Tabella frequenza estesa
- 3 Distribuzione di frequenza
- 3.1 Distribuzione della frequenza per dati raggruppati
- 4 Esempio
- 5 Esercizio risolto
- 5.1 Soluzione
- 6 Riferimenti
Formule
La frequenza assoluta, indicata come fio, è uguale al numero di volte che un certo valore Xio è all'interno del gruppo di osservazioni.
Supponendo che il totale delle osservazioni sia N valori, la somma di tutte le frequenze assolute deve essere uguale a questo numero:
∑fio = f1 + FDue + F3 +... fn = N
Altre frequenze
Se ogni valore di fio diviso per il numero totale di dati N, abbiamo il frequenza relativa Fr del valore X.io:
Fr = fio / N
Le frequenze relative sono valori compresi tra 0 e 1, perché N è sempre maggiore di qualsiasi fio, ma la somma deve essere uguale a 1.
Moltiplicando ogni valore di f per 100r tu hai il frequenza relativa percentuale, la cui somma è del 100%:
Frequenza relativa percentuale = (fio / N) x 100%
Altrettanto importante è frequenza cumulativa Fio fino ad una certa osservazione, questa è la somma di tutte le frequenze assolute fino a detta osservazione inclusa:
Fio = f1 + FDue + F3 +... fio
Se la frequenza accumulata è divisa per il numero totale di dati N, abbiamo il frequenza relativa cumulativa, che moltiplicato per 100 dà il frequenza relativa cumulativa percentuale.
Come ottenere la frequenza assoluta?
Per trovare la frequenza assoluta di un certo valore che appartiene a un set di dati, tutti sono organizzati dal più basso al più alto e viene conteggiato il numero di volte in cui il valore appare.
Nell'esempio delle taglie dei vestiti, la frequenza assoluta della taglia 4 è di 3 abiti, cioè f1 = 3. Per la taglia 6, sono stati venduti 4 abiti: fDue = 4. Nella taglia 8 sono stati venduti anche 4 abiti, f3 = 4 e così via.
Tabulazione
I risultati totali possono essere rappresentati in una tabella che mostra le frequenze assolute di ciascuno:
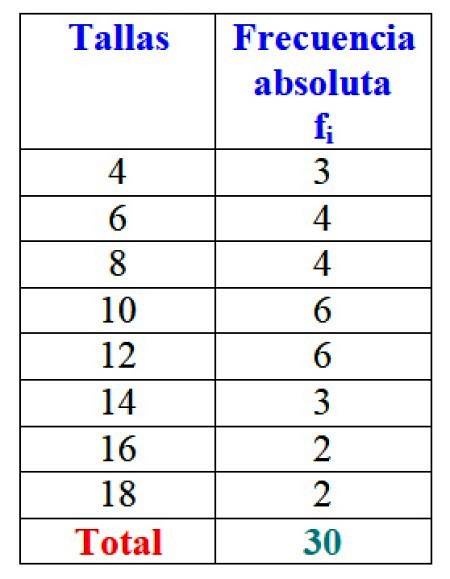
Ovviamente è vantaggioso organizzare le informazioni e poterle accedere a colpo d'occhio, invece di lavorare con i singoli dati.
Importante: si noti che quando si aggiungono tutti i valori della colonna fio ottieni sempre il numero totale di dati. In caso contrario, devi controllare la contabilità, poiché c'è un errore.
Tabella delle frequenze estesa
La tabella sopra può essere estesa aggiungendo gli altri tipi di frequenza nelle colonne successive a destra:
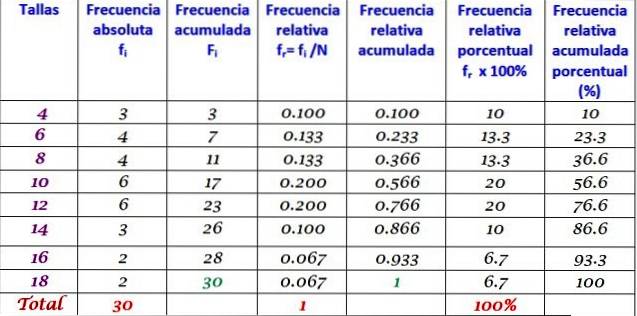
Distribuzione di frequenza
La distribuzione delle frequenze è il risultato dell'organizzazione dei dati in termini di frequenze. Quando si lavora con molti dati, è conveniente raggrupparli in categorie, intervalli o classi, ciascuno con le rispettive frequenze: assoluta, relativa, accumulata e percentuale..
L'obiettivo di farli è quello di accedere più facilmente alle informazioni contenute nei dati, nonché di interpretarli correttamente, cosa che non è possibile quando sono presentati in ordine non ordinato..
Nell'esempio delle dimensioni, i dati non sono raggruppati in quanto non sono troppe dimensioni e possono essere facilmente manipolati e contabilizzati. Anche le variabili qualitative possono essere lavorate in questo modo, ma quando i dati sono molto numerosi è meglio lavorare raggruppandole in classi.
Distribuzione della frequenza per dati raggruppati
Per raggruppare i tuoi dati in classi di uguale dimensione, considera quanto segue:
-Dimensioni, larghezza o ampiezza della classe: è la differenza tra il valore più alto della classe e il valore più basso.
La dimensione della classe si decide dividendo il rango R per il numero di classi da considerare. L'intervallo è la differenza tra il valore massimo dei dati e il più piccolo, in questo modo:
Dimensione della classe = Rango / Numero di classi.
-Limite di classe: intervallo dal limite inferiore al limite superiore della classe.
-Voto di classe: è il punto medio dell'intervallo, considerato rappresentativo della classe. Viene calcolato con la semisomma del limite superiore e del limite inferiore della classe.
-Numero di classi: La formula di Sturges può essere utilizzata:
Numero di classi = 1 + 3.322 log N
Dove N è il numero di classi. Poiché di solito è un numero decimale, viene arrotondato al numero intero successivo.
Esempio
Una macchina in una grande fabbrica è fuori servizio a causa di guasti ricorrenti. Di seguito si registrano i periodi consecutivi di inattività in minuti, di detta macchina, con un totale di 100 dati:
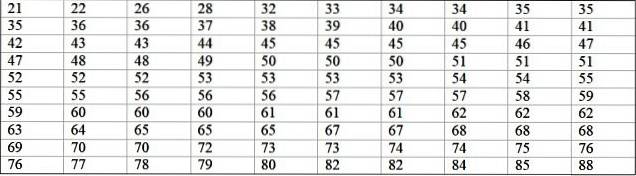
Per prima cosa viene determinato il numero di classi:
Numero di classi = 1 + 3.322 log N = 1 + 3,32 log 100 = 7,64 ≈ 8
Dimensione delle classi = Intervallo / Numero di classi = (88-21) / 8 = 8.375
È anche un numero decimale, quindi 9 è considerato la dimensione della classe.
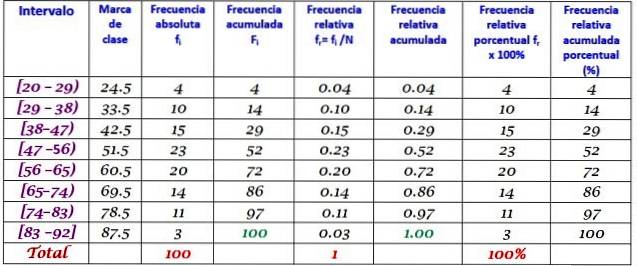
Il voto di classe è la media tra i limiti superiore e inferiore della classe, ad esempio per la classe [20-29) c'è un voto di:
Voto di classe = (29 + 20) / 2 = 24,5
Procediamo allo stesso modo per trovare i voti di classe degli intervalli rimanenti.
Esercizio risolto
40 giovani hanno indicato che il tempo in minuti trascorsi su Internet domenica scorsa è stato il seguente, in ordine crescente:
0; 12; venti; 35; 35; 38; 40; Quattro cinque; 45, 45; 59; 55; 58; 65; 65; 70; 72; 90; 95; 100; 100; 110; 110; 110; 120; 125; 125; 130; 130; 130; 150; 160; 170; 175; 180; 185; 190; 195; 200; 220.
Viene chiesto di costruire la distribuzione di frequenza di questi dati.
Soluzione
L'intervallo R dell'insieme di N = 40 dati è:
R = 220 - 0 = 220
Applicando la formula di Sturges per determinare il numero di classi si ottiene il seguente risultato:
Numero di classi = 1 + 3.322 log N = 1 + 3.32 log 40 = 6.3
Poiché è un decimale, il numero intero immediato è 7, quindi i dati sono raggruppati in 7 classi. Ogni classe ha una larghezza di:
Dimensione delle classi = Grado / Numero di classi = 220/7 = 31,4
Un valore di chiusura e arrotondamento è 35, quindi viene scelta una larghezza di classe di 35.
I voti di classe vengono calcolati facendo la media dei limiti superiore e inferiore di ciascun intervallo, ad esempio, per l'intervallo [0,35):
Voto di classe = (0 + 35) / 2 = 17,5
Procedi allo stesso modo con le altre classi.
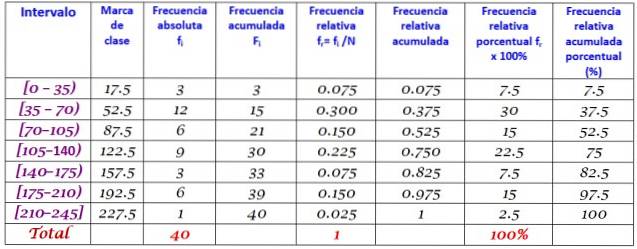
Infine, le frequenze vengono calcolate secondo la procedura sopra descritta, ottenendo la seguente distribuzione:
Riferimenti
- Berenson, M. 1985. Statistiche per la gestione e l'economia. Interamericana S.A.
- Devore, J. 2012. Probabilità e statistica per l'ingegneria e la scienza. 8 °. Edizione. Cengage.
- Levin, R. 1988. Statistics for Administrators. 2 °. Edizione. Prentice Hall.
- Spiegel, M. 2009. Statistiche. Serie Schaum. 4 ° Edizione. Mcgraw hill.
- Walpole, R. 2007. Probabilità e statistica per l'ingegneria e le scienze. Pearson.



Nessun utente ha ancora commentato questo articolo.