
Flusso di campo elettrico
Cos'è il flusso di campo elettrico?
Il flusso del campo elettrico o semplicemente il flusso elettrico è una quantità scalare proporzionale al numero di linee di campo elettrico che passano attraverso una superficie. È indicato dalla lettera greca maiuscola Φ (phi).
Il campo elettrico in realtà non "fluisce" nel modo in cui fa un flusso d'acqua, sebbene le correnti del fluido assomiglino a quelle del campo elettrico..
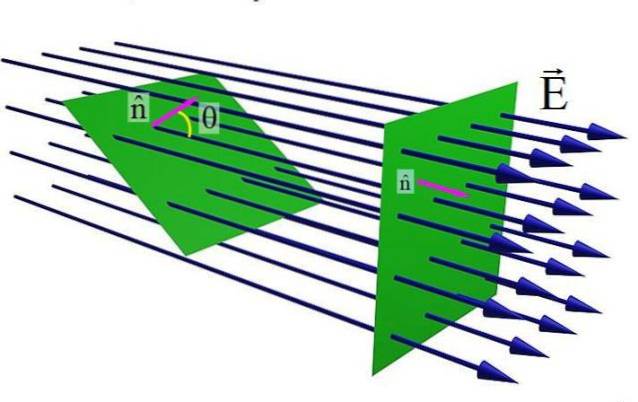
La figura sopra mostra una superficie piana attraversata da un campo elettrico E. Quando il vettore unitario normale alla superficie n e il campo E sono parallele, il numero di linee di campo che attraversano la superficie è massimo. Ma come l'angolo θ tra n Y E, il numero di linee che passano per la superficie verde è inferiore.
D'altra parte, il flusso del campo elettrico dipende anche dall'entità di E, perché più è grande, più linee di campo attraversano la superficie. E ovviamente, maggiore è l'area S di detta superficie, maggiore è il flusso, quindi si stabilisce la seguente equazione:
Φ = E ∙ Scosθ
Questa espressione è coerente con il prodotto scalare tra i vettori E Y n:
Φ = (E • n) S
L'unità per il flusso del campo elettrico nel Sistema internazionale di unità di misura SI è N.mDue/ C (newton x metro quadrato / coulomb). In alternativa, poiché il campo è misurato anche in V / m (volt su metro), il flusso elettrico rimane in (V ∙ m).
Esempi
Secondo la definizione, il flusso elettrico può essere positivo, negativo o uguale a 0. Il flusso del campo elettrico è:
-Positivo quando l'angolo θ è compreso tra E Y n è inferiore a 90º, poiché cos θ è maggiore di zero.
-Negativo se detto angolo è maggiore di 90º, perché allora cos θ è minore di zero.
-Null quando θ è esattamente 90º, perché cos 90º = 0 e le linee di campo in questo caso sono tangenziali alla superficie.
-D'altra parte, se l'angolo tra E Y n è uguale a 0, il flusso acquisisce il suo valore massimo.
Queste possibilità sono mostrate nell'immagine seguente:
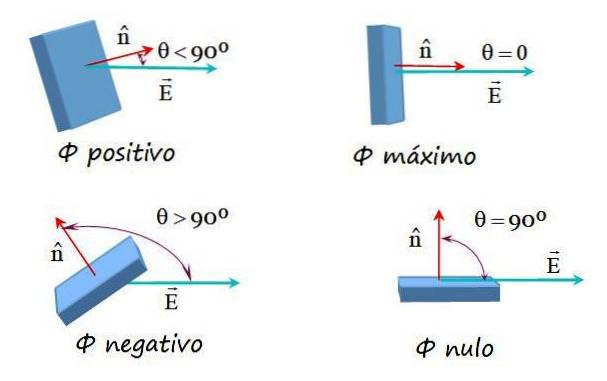
Flusso di campo elettrico su una superficie arbitraria
In precedenza, il flusso del campo elettrico veniva determinato nel caso particolare di un incidente di campo uniforme su una superficie piana. Per una superficie di forma arbitraria S e / o un campo elettrico non uniforme, l'angolo tra E Y n può variare da punto a punto.
Nella figura seguente ci sono due esempi, a sinistra una superficie curva ea destra una superficie chiusa.
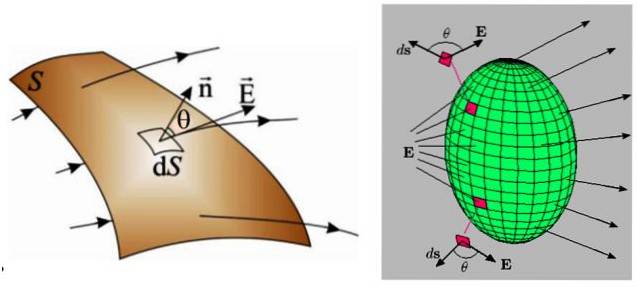
In entrambi i casi, la superficie è suddivisa in regioni molto più piccole, di dimensione infinitesimale, dette dS, attraverso le quali passa un flusso anche infinitesimale dΦ:
dΦ = (E•n) dS = (Ecosθ) dS
Il campo totale si ottiene sommando tutti questi contributi infinitesimali:


In caso di superfici chiuse, n punta sempre verso l'esterno, quindi il flusso ha segno + quando è saliente ad S, essendo l'angolo tra E Y n è inferiore a 90º, e segno - quando il campo è in arrivo, perché allora l'angolo tra E Y n è maggiore di 90º (vedi figura 2).
Notare che nella superficie chiusa a destra, il numero di linee di campo che entrano nella superficie è uguale al numero di linee in uscita. Pertanto il flusso netto, definito come la somma algebrica del flusso in entrata e del flusso in uscita, è zero.
La sorgente del campo elettrico in questo caso è all'esterno della superficie, tuttavia, il flusso netto sarebbe diverso da 0 se la sorgente del campo elettrico (la distribuzione delle cariche) fosse all'interno della superficie..
Formazione
Esercizio 1
Ha un campo elettrico E = 3,5 kN / C X e una superficie rettangolare piana di 0,35 m di larghezza per 0,7 m di lunghezza. Trova il flusso del campo elettrico attraverso il rettangolo nei seguenti casi:
a) La superficie è parallela al piano yz.
b) Il rettangolo è parallelo al piano xy.
c) La normale del piano forma un angolo di 40º con l'asse x e contiene l'asse y.

Soluzione a
Il vettore normale e il vettore del campo elettrico sono paralleli, quindi l'angolo θ tra di loro è 0º e il flusso elettrico è:
Φ = (E ∙ S) cos 0 = E ∙ S
L'area S del rettangolo è:
S = 0,35 m x 0,7 m = 0,245 mDue
Sostituzione in Φ:
Φ = E ∙ S = 3,5 x 103 N / C × 0,245 mDue = 857,5 N ∙ mDue / C.
Soluzione b
Il flusso del campo elettrico è 0, poiché i vettori E Y n sono perpendicolari tra loro.
Soluzione c
L'angolo θ tra il campo E e il vettore normale n è 40º (vedi figura), quindi:
Φ = E ∙ S ∙ cos θ = 3,5 x 103 N / C × 0,245 mDue × cos 40º = 656,9 N ∙ mDue / C.
Esercizio 2
Calcola il flusso del campo elettrico che produce una carica puntiforme positiva qo = 2μC situata al centro di una sfera di raggio R = 5 cm.
Soluzione
Il campo prodotto dalla carica qo Non è uniforme, ma dalla legge di Coulomb si sa che sulla superficie della sfera ha una grandezza di:
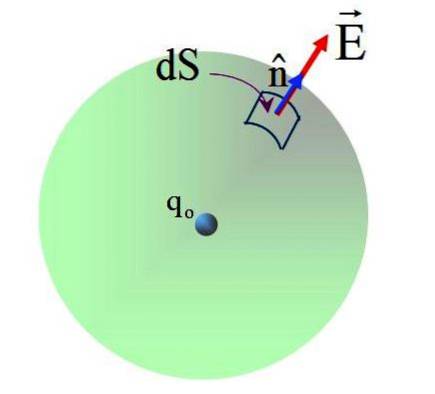

Il campo ha una direzione radiale e il vettore normale n, quindi l'angolo tra entrambi i vettori è 0 in ogni punto della superficie sferica. Sostituzione in:

Deve:

L'integrale di dS sull'intera superficie sferica S è la sua area, che è 4πRDue, Quindi:

Il suo valore è:
Φ = 4π × 9 × 109 x 2 × 10-6 N⋅mDue/ C = 2,3 x 105 N⋅mDue/ C
Riferimenti
- Bauer, W. 2011. Fisica per l'ingegneria e le scienze. Volume 1. Mc Graw Hill.
- Figueroa, D. (2005). Serie: Fisica per la scienza e l'ingegneria. Volume 5. Elettrostatica. A cura di Douglas Figueroa (USB).
- Giambattista, A. 2010. Fisica. 2 °. Ed. McGraw Hill.
- Giancoli, D. 2006. Fisica: principi con applicazioni. 6 °. Ed prentice hall.
- Sears, Zemansky. 2016. Fisica universitaria con fisica moderna. 14th. Ed. Volume 1. Pearson.



Nessun utente ha ancora commentato questo articolo.