Il errore standard di stima misura la deviazione in un valore di popolazione campione. Cioè, l'errore standard di stima misura le possibili variazioni della media campionaria rispetto al valore reale della media della popolazione..
Ad esempio, se vuoi conoscere l'età media della popolazione di un paese (popolazione media), prendi un piccolo gruppo di abitanti, che chiameremo “campione”. Da esso si estrae l'età media (media campionaria) e si assume che la popolazione abbia quell'età media con un errore standard di stima che varia più o meno.
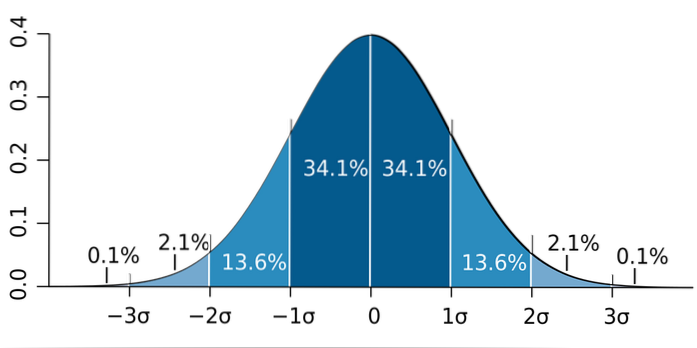
Va notato che è importante non confondere la deviazione standard con l'errore standard e con l'errore standard di stima:
1- La deviazione standard è una misura della dispersione dei dati; cioè, è una misura della variabilità della popolazione.
2- L'errore standard è una misura della variabilità del campione, calcolata sulla base della deviazione standard della popolazione.
3- L'errore standard di stima è una misura dell'errore che viene commesso quando si prende la media campionaria come stima della media della popolazione.
Indice articolo
L'errore standard di stima può essere calcolato per tutte le misurazioni ottenute nei campioni (ad esempio, errore standard di stima della media o errore standard di stima della deviazione standard) e misura l'errore commesso durante la stima della popolazione reale misurare dal suo valore campione
Dall'errore standard di stima, viene costruito l'intervallo di confidenza della misura corrispondente.
La struttura generale di una formula per l'errore standard di stima è la seguente:
Errore standard di stima = ± Coefficiente di confidenza * Errore standard
Coefficiente di confidenza = valore limite di una statistica campione o distribuzione campionaria (campana normale o gaussiana, t di Student, tra gli altri) per un dato intervallo di probabilità.
Errore standard = deviazione standard della popolazione divisa per la radice quadrata della dimensione del campione.
Il coefficiente di confidenza indica il numero di errori standard che sei disposto ad aggiungere e sottrarre alla misura per avere un certo livello di fiducia nei risultati..
Supponiamo che tu stia cercando di stimare la percentuale di persone nella popolazione che hanno un comportamento A e che tu voglia avere il 95% di fiducia nei tuoi risultati..
Si preleva un campione di n persone e si determina la proporzione campionaria p e il suo complemento q.
Errore standard di stima (SEE) = ± Coefficiente di confidenza * Errore standard
Coefficiente di fiducia = z = 1,96.
Errore standard = la radice quadrata del rapporto tra il prodotto della proporzione del campione e il suo complemento e la dimensione del campione n.
Dall'errore standard di stima, viene stabilito l'intervallo in cui ci si aspetta di trovare la proporzione della popolazione o la proporzione del campione di altri campioni che possono essere formati da quella popolazione, con un livello di confidenza del 95%:
p - EEE ≤ Proporzione popolazione ≤ p + EEE
1- Supponiamo che tu stia cercando di stimare la percentuale di persone nella popolazione che hanno una preferenza per una formula di latte arricchito e che tu voglia avere il 95% di fiducia nei tuoi risultati..
Viene prelevato un campione di 800 persone e 560 persone nel campione sono determinate a preferire la formula del latte fortificato. Determinare un intervallo in cui ci si può aspettare di trovare la proporzione della popolazione e la proporzione di altri campioni che possono essere prelevati dalla popolazione, con una confidenza del 95%
a) Calcoliamo la proporzione campionaria p e il suo complemento:
p = 560/800 = 0,70
q = 1 - p = 1 - 0,70 = 0,30
b) È noto che la proporzione approssima una distribuzione normale a campioni di grandi dimensioni (maggiori di 30). Quindi, viene applicata la cosiddetta regola 68-95 - 99.7 e dobbiamo:
Coefficiente di fiducia = z = 1,96
Errore standard = √ (p * q / n)
Errore standard di stima (SEE) = ± (1,96) * √ (0,70) * (0,30) / 800) = ± 0,0318
c) Dall'errore standard di stima, viene stabilito l'intervallo in cui ci si aspetta di trovare la proporzione della popolazione con un livello di confidenza del 95%:
0,70 - 0,0318 ≤ Proporzione popolazione ≤ 0,70 + 0,0318
0,6682 ≤ Proporzione popolazione ≤ 0,7318
La proporzione del campione del 70% può variare fino a 3,18 punti percentuali se si prende un campione diverso di 800 individui o se la proporzione effettiva della popolazione è compresa tra 70 - 3,18 = 66,82% e 70 + 3,18 = 73,18%.
2- Tratteremo da Spiegel e Stephens, 2008, il seguente caso di studio:
È stato prelevato un campione casuale di 50 voti dal totale dei voti in matematica degli studenti del primo anno di un'università, in cui la media rilevata era di 75 punti e la deviazione standard di 10 punti. Quali sono i limiti di confidenza del 95% per la stima dei voti medi di matematica del college??
a) Calcoliamo l'errore standard di stima:
Coefficiente di confidenza del 95% = z = 1,96
Errore standard = s / √n
Errore standard di stima (SEE) = ± (1,96) * (10√50) = ± 2,7718
b) Dall'errore standard di stima, viene stabilito l'intervallo in cui si prevede di trovare la media della popolazione o la media di un altro campione di dimensione 50, con un livello di confidenza del 95%:
50 - 2,7718 ≤ Media della popolazione ≤ 50 + 2,7718
47.2282 ≤ Media della popolazione ≤ 52,7718
c) La media campionaria può variare fino a 2,7718 punti se viene preso un campione diverso di 50 voti o se la media effettiva dei voti in matematica della popolazione universitaria è compresa tra 47.2282 punti e 52.7718 punti.
Nessun utente ha ancora commentato questo articolo.