
Formule ed equazioni di errore di campionamento, calcoli, esempi
Il errore di campionamento o errore di esempio In statistica, è la differenza tra il valore medio di un campione e il valore medio della popolazione totale. Per illustrare l'idea, immaginiamo che la popolazione totale di una città sia un milione di persone, di cui si vuole la misura media delle scarpe, per la quale si prende un campione casuale di mille persone.
La dimensione media che emerge dal campione non coinciderà necessariamente con quella della popolazione totale, anche se se il campione non è sbilanciato il valore deve essere vicino. Questa differenza tra il valore medio del campione e quello della popolazione totale è l'errore di campionamento.
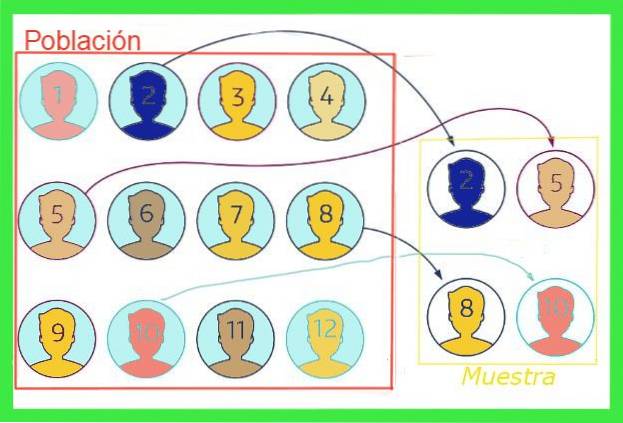
In generale, il valore medio della popolazione totale è sconosciuto, ma esistono tecniche per ridurre questo errore e formule per stimarlo margine di errore di campionamento che sarà esposto in questo articolo.
Indice articolo
- 1 Formule ed equazioni
- 2 Come calcolare l'errore di campionamento
- 2.1 Per un livello di confidenza γ
- 3 esempi
- 3.1 - Esempio 1
- 3.2 - Esempio 2
- 3.3 - Esempio 3
- 3.4 - Esempio 4
- 3.5 - Esercizio 5
- 4 Riferimenti
Formule ed equazioni
Supponiamo che tu voglia conoscere il valore medio di una certa caratteristica misurabile X in una popolazione di dimensioni N, ma come N è un numero elevato, non è possibile effettuare lo studio sulla popolazione totale, quindi si procede a prendere a campione aleatorio di dimensioni n<
Il valore medio del campione è indicato con
Supponiamo che prendano m campioni dalla popolazione totale N, tutte le stesse dimensioni n con valori medi
Questi valori medi non saranno identici tra loro e saranno tutti intorno al valore medio della popolazione μ. Il margine di errore di campionamento E indica la separazione attesa dei valori medi
Il margine di errore standard ε campione di dimensioni n è:
ε = σ / √n
dove σ è la deviazione standard (la radice quadrata della varianza), che viene calcolata utilizzando la seguente formula:
σ = √ [(x -
Il significato di margine di errore standard ε è il seguente:
Il valore medio
Come calcolare l'errore di campionamento
Nella sezione precedente è stata data la formula per trovare il file intervallo di errore standard di un campione di dimensione n, dove la parola standard indica che si tratta di un margine di errore con una confidenza del 68%.
Ciò indica che se sono stati prelevati molti campioni della stessa dimensione n, Il 68% di loro darà valori medi
C'è una regola semplice, chiamata regola 68-95-99.7 che ci permette di trovare il margine di errore di campionamento E per livelli di confidenza di 68%, 95% Y 99,7% facilmente, poiché questo margine è 1⋅ε, 2⋅ε e 3⋅ε rispettivamente.
Per un livello di fiducia γ
Se lui livello di confidenza γ non è nessuno dei precedenti, quindi l'errore di campionamento è la deviazione standard σ moltiplicato per il fattore Zγ, che si ottiene con la seguente procedura:
1.- Prima il file livello di significatività α che viene calcolato da livello di confidenza γ utilizzando la seguente relazione: α = 1 - γ
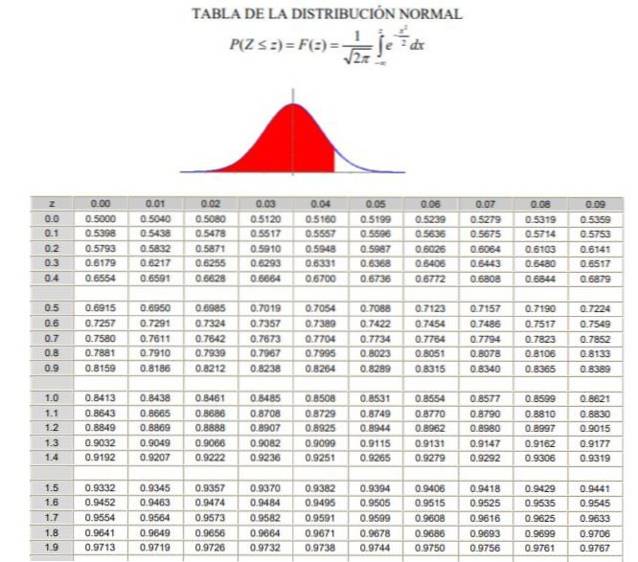
2.- Quindi devi calcolare il valore 1 - α / 2 = (1 + γ) / 2, che corrisponde alla frequenza normale accumulata tra -∞ e Zγ, in una distribuzione gaussiana normale o standardizzata F (z), la cui definizione può essere vista in figura 2.
3.- L'equazione è risolta F (Zγ) = 1 - α / 2 tramite le tabelle della distribuzione normale (cumulativa) F, oppure tramite un'applicazione informatica che ha la funzione gaussiana standardizzata inversa F-1.
In quest'ultimo caso abbiamo:
Zγ = G-1(1 - α / 2).
4.- Infine, questa formula viene applicata per l'errore di campionamento con un livello di affidabilità γ:
E = Zγ⋅(σ / √n)
Esempi
- Esempio 1
Calcola il margine di errore standard nel peso medio di un campione di 100 neonati. Il calcolo del peso medio è stato
Soluzione
Il margine di errore standard è ε = σ / √n = (1.500 kg) / √100 = 0,15 kg. Il che significa che con questi dati si può desumere che il peso del 68% dei neonati è compreso tra 2.950 kg e 3,25 kg.
- Esempio 2
Determinare il margine di errore di campionamento E e l'intervallo di peso di 100 neonati con un livello di confidenza del 95% se il peso medio è di 3.100 kg con deviazione standard σ = 1.500 kg.
Soluzione
Se la regola 68; 95; 99,7 → 1⋅ε; 2⋅ε; 3⋅ε, avete:
E = 2⋅ε = 2⋅0,15 kg = 0,30 kg
Cioè, il 95% dei neonati avrà un peso compreso tra 2.800 kg e 3.400 kg.
- Esempio 3
Determina l'intervallo di peso dei neonati dall'Esempio 1 con un margine di confidenza del 99,7%.
Soluzione
L'errore di campionamento con una confidenza del 99,7% è 3 σ / √n, che per il nostro esempio è E = 3 * 0,15 kg = 0,45 kg. Da qui si deduce che il 99,7% dei neonati avrà un peso compreso tra 2.650 kg e 3.550 kg.
- Esempio 4
Determina il fattore Zγ per un livello di affidabilità del 75%. Determina il margine di errore di campionamento con questo livello di affidabilità per il caso presentato nell'esempio 1.
Soluzione
Il livello di confidenza è γ = 75% = 0,75 che è correlato al livello di significatività α attraverso la relazione γ= (1 - α), in modo che il livello di significatività sia α = 1 - 0,75 = 0,25.
Ciò significa che la probabilità normale cumulativa tra -∞ e Zγ è:
P (Z ≤ Zγ ) = 1 - 0.125 = 0,875
Ciò che corrisponde a un valore Zγ 1.1503, come mostrato nella Figura 3.
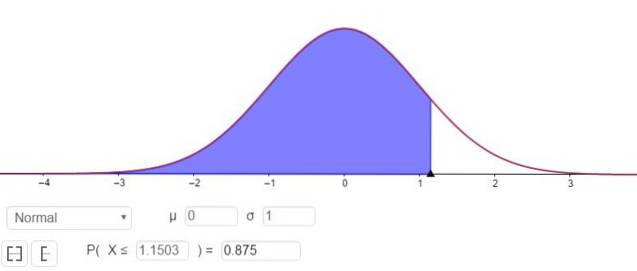
Cioè, l'errore di campionamento è E = Zγ⋅(σ / √n)= 1.15⋅(σ / √n).
Quando applicato ai dati dell'esempio 1, restituisce un errore di:
E = 1,15 * 0,15 kg = 0,17 kg
Con un livello di fiducia del 75%.
- Esercizio 5
Qual è il livello di confidenza se Zα / 2 = 2.4 ?
Soluzione
P (Z ≤ Zα / 2 ) = 1 - α / 2
P (Z ≤ 2,4) = 1 - α / 2 = 0,9918 → α / 2 = 1 - 0,9918 = 0,0082 → α = 0,0164
Il livello di significatività è:
α = 0,0164 = 1,64%
E infine, il livello di fiducia rimane:
1- α = 1 - 0,0164 = 100% - 1,64% = 98,36%
Riferimenti
- Canavos, G. 1988. Probabilità e statistica: applicazioni e metodi. Mcgraw hill.
- Devore, J. 2012. Probabilità e statistica per l'ingegneria e la scienza. 8 °. Edizione. Cengage.
- Levin, R. 1988. Statistics for Administrators. 2 °. Edizione. Prentice Hall.
- Sudman, S. 1982. Fare domande: una guida pratica alla progettazione del questionario. San Francisco. Jossey basso.
- Walpole, R. 2007. Probabilità e statistica per l'ingegneria e le scienze. Pearson.
- Wonnacott, T.H. e R.J. Wonnacott. 1990. Statistiche introduttive. 5a Ed. Wiley
- Wikipedia. Errore di campionamento. Estratto da: en.wikipedia.com
- Wikipedia. Margine di errore. Estratto da: en.wikipedia.com



Nessun utente ha ancora commentato questo articolo.