Si afferma che si trovi un corpo esteso equilibrio rotazionale quando la somma delle coppie che agiscono su di essa è zero. Ciò non significa che l'oggetto sia necessariamente fermo, ma piuttosto che non vi è alcuna tendenza netta a cambiare il suo stato di movimento per un altro..
Un oggetto che si muove a velocità costante lo fa lungo una linea retta e possiamo considerarlo in equilibrio rotazionale. Ora, gli oggetti ruotano perché ci sono forze che agiscono su di essi in modo tale che ne risulta una rotazione. La capacità di una forza di produrre rotazione, chiamata coppia o torca, dipende non solo dall'intensità della forza, ma anche da dove viene applicata.
Lo riconosciamo subito quando si vuole aprire una porta chiusa: la forza non viene mai applicata vicino ai cardini, ma lontano da essi, per questo motivo la maniglia è posizionata il più lontano possibile, sul lato opposto della porta.
L'asse di rotazione della porta passa attraverso le cerniere. Insistendo per spingerlo molto vicino ai cardini, ci vuole un grande sforzo per far muovere la porta anche un po '..
In letteratura, la coppia si trova sotto diversi nomi: coppia, torsione, momento di una forza e coppia. Sono tutti sinonimi.
Quindi, abbiamo bisogno di conoscere le coppie che agiscono su un oggetto per stabilire la condizione di equilibrio rotazionale.
Indice articolo
La condizione di equilibrio rotazionale è:
La somma di tutti i momenti o coppie che agiscono su un corpo, calcolati rispetto ad un qualsiasi asse, deve essere zero.
L'oggetto in questione deve essere allungato, poiché le particelle, per definizione, hanno solo equilibrio traslazionale.
Possono esserci forze applicate al corpo ed esiste ancora un equilibrio rotazionale, purché le forze non lo facciano ruotare.
Può esserci anche movimento, anche accelerato, ma sempre lungo una linea retta, poiché non tutte le forze provocano la comparsa di coppie. Questi compaiono quando le forze non agiscono tutte lungo la stessa linea di azione..
La coppia è indicata dalla lettera greca τ, sopra carattere in grassetto perché è un vettore e quindi lo distinguiamo dalla sua grandezza o modulo, che è uno scalare. Dipende dalla forza applicata F, vettore r cioè diretto dall'asse di rotazione O al punto di applicazione della forza e, infine, dall'angolo tra questi due vettori.
Il prodotto vettore stabilisce la relazione appropriata tra queste quantità:
τ = r X F
E il modulo di coppia, indicato senza grassetto, è:
τ = r⋅F⋅sen θ
Dove θ è l'angolo tra r Y F. Le unità di coppia sono semplicemente N⋅m nel sistema internazionale.
Nella figura è presente una chiave con cui si intende ruotare un dado in senso antiorario (senso antiorario). Per questo viene testato con due forze FPER Y FB.
FPER è più vicino a O e ha un vettore rPER o braccio di leva più corto, quindi non produce tanta coppia quanto la forza FB, che ha uguale grandezza, ma ha un vettore rB più grandi.
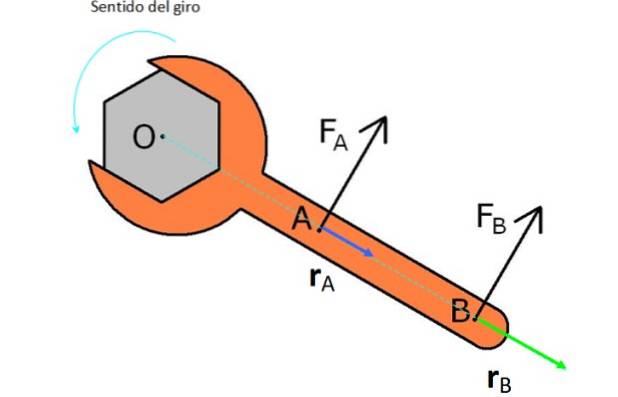
Nota che se vuoi ruotare il dado in senso orario, devi applicare le forze nella direzione opposta a come appaiono in figura.
Poiché la coppia risulta dal prodotto incrociato tra la forza e i vettori di posizione, e questi sono nel piano della chiave, la coppia deve essere un vettore perpendicolare a detto piano, cioè diretto verso il lettore o verso l'interno del pagina.
Per convenzione, la coppia è positiva se ruota in senso antiorario e negativa se ruota in senso orario..
La direzione e il senso della coppia risultante sono facilmente determinati dalla regola della mano destra mostrata di seguito:
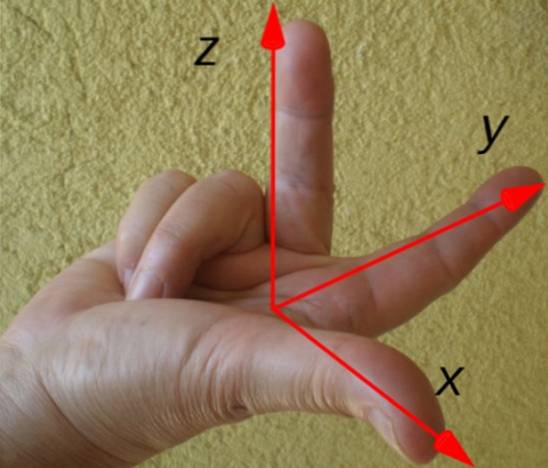
Il dito indice punta in base al vettore di posizione r, dito medio in base alla forza F e il pollice indica la direzione e il senso della coppia τ. In questo esempio, la coppia è diretta lungo l'asse x, secondo il disegno degli assi delle coordinate.
Se le coppie agiscono su un corpo τ1, τDue, τ3 ... τio, la coppia netta o risultante τn è la somma vettoriale di tutti loro:
τn = τ1+ τDue + τ3 +... τio
Con la notazione di sommatoria rimane:
τn = ∑ τio
La condizione di equilibrio è espressa matematicamente come segue:
τn = 0
O bene:
∑ τio = 0
Dove la coppia τ, rispetto ad un certo asse O, viene calcolato da:
τ = r X F
E la cui grandezza è:
τ = r⋅F⋅sen θ
-Negli esseri umani e negli animali, il peso è una forza che può causare torsione, rotazione e caduta.
Le persone generalmente mantengono una postura tale che quando camminano, le mantengono in equilibrio rotazionale, a meno che non praticano attività sportive, come ginnastica, pattinaggio o sport in generale..
-Due ragazzi che sono riusciti a rimanere orizzontali nel rocker o su e giù sono in equilibrio rotazionale.
-Quando i piatti della bilancia sono bilanciati, il sistema è in equilibrio rotazionale.
-Anche segnali e semafori appesi su strade e viali sono in equilibrio rotazionale. Se i cavi che li trattengono si rompono, questo equilibrio si perde e il cartello si blocca o cade..
-Ponti sospesi come il Golden Gate di San Francisco e il ponte nella Figura 1.
La barra di supporto mostrata in figura è molto leggera. La forza esercitata dal supporto è F e all'estrema destra viene applicata la forza PER.
Si richiede di calcolare le grandezze di queste forze considerando che il sistema è in equilibrio traslazionale e rotazionale.
Poiché il sistema non si muove, la somma delle forze viene annullata. Sono tutti verticali e possono essere lavorati con le grandezze. La direzione positiva è verso l'alto e la direzione negativa è verso il basso, quindi:
F - 80 - LA = 0
Ora viene applicata la condizione di equilibrio rotazionale, per la quale dobbiamo scegliere un asse di rotazione arbitrario. In questo caso, viene scelto all'estrema destra, in modo che il vettore rPER è nulla, in questo modo la coppia esercitata da PER, ma solo quelli di F e la forza della sinistra.
La coppia prodotta da F è, secondo la regola della mano destra e il sistema di coordinate mostrato:
τF = rF X F = 0,9 F (-K) N.m
È diretto verso l'interno dello schermo e presenta un segno negativo. Mentre la coppia prodotta dalla forza di 80 N è:
τ = 80 x 1,20 (K) N⋅m = 96 (K) N⋅m
Questa coppia è diretta lontano dallo schermo e riceve un segno positivo. Come esiste l'equilibrio rotazionale:
96 - 0,9⋅F = 0
La grandezza di F è:
F = (96 / 0,9) N = 106,7 N
E poiché il sistema è in equilibrio traslazionale, la somma delle forze si annulla. Questo ci consente di risolvere per l'entità di PER:
F - A - 80 N = 0
Perciò:
A = 106,7 - 80 N = 26,7 N.
Nessun utente ha ancora commentato questo articolo.