
Condizioni di equilibrio traslazionale, esempi, esercizi
Si afferma che si trovi un oggetto equilibrio traslazionale quando la somma delle forze che agiscono su di essa è zero. Ciò non significa che ci sia necessariamente riposo, ma il movimento, se esiste, sarebbe rettilineo uniforme o esclusivamente rotazionale, nel caso di un oggetto di grandi dimensioni..
Le condizioni di equilibrio meccanico si basano sulle leggi della meccanica di Newton. Infatti, la prima legge ci dice che un oggetto è fermo o si muove con moto rettilineo uniforme MRU, a condizione che nessuna forza netta agisca su di esso.

Ora, la forza netta o forza risultante è semplicemente la somma vettoriale di tutte le forze che agiscono sull'oggetto. Secondo la seconda legge di Newton, questa somma deve essere uguale al prodotto tra la massa e l'accelerazione, ma se l'oggetto non è accelerato, questa somma svanisce.
E in assenza di accelerazione, ci sono le due possibilità di cui sopra: il corpo è a riposo, cioè non si muove, o se lo fa, deve essere con MRU. Nel primo caso si parla di equilibrio transnazionale statico e nel secondo di dinamico.
L'equilibrio traslazionale è un fattore importante in molti aspetti dell'ingegneria, ad esempio nella costruzione. Gli elementi che compongono un edificio: travi, cavi, telai e altro, devono essere in equilibrio per garantire la stabilità dell'involucro.
L'equilibrio traslazionale è ricercato anche nelle strutture mobili, come scale mobili, nastri trasportatori e nella pratica di numerosi sport..
Indice articolo
- 1 Condizione di equilibrio traslazionale
- 1.1 Diagrammi a corpo libero
- 2 Esempi di equilibrio traslazionale
- 2.1 Edifici e strade
- 2.2 Libri e oggetti sugli scaffali
- 2.3 I mobili
- 2.4 Semafori
- 2.5 Illuminazione pubblica
- 3 Esercizio risolto
- 3.1 Soluzione
- 4 Riferimenti
Condizione di equilibrio traslazionale
Supponiamo che diverse forze agiscano su un corpo, che indichiamo come F1, FDue, F3... . Fn, utilizzando il grassetto per evidenziare il fatto che le forze sono vettori e devono essere aggiunte come tali.
Viene chiamata la somma vettoriale di tutte queste forze forza risultante o forza netta. Se questa somma risulta nel vettore nullo, la condizione per l'equilibrio traslazionale è soddisfatta:
F1+ FDue+ F3... .+ Fn = 0
Questa condizione può essere scritta in modo compatto utilizzando la notazione di sommatoria:
∑ Fio = 0
In termini di componenti della forza risultante, l'equazione di cui sopra, che è vettore, può essere scomposta in tre equazioni scalari, una per ogni componente della forza risultante:
∑ Fix = 0; ∑ FY = 0 e ∑ Fz = 0
In pratica, non è facile annullare la somma delle forze, perché l'attrito è una forza di contatto tra superfici che difficilmente viene annullata completamente da qualsiasi altra forza..
Questo è il motivo per cui gli oggetti reali non sono quasi mai esenti da forze esterne, e di conseguenza è difficile ottenere l'equilibrio traslazionale.
Quindi gli ingegneri usano meccanismi per ridurre l'attrito, come i cuscinetti e l'uso di oli lubrificanti..
Diagrammi a corpo libero
Il diagramma del corpo libero è un diagramma in cui vengono disegnate le forze che agiscono sul corpo. Quando si cerca l'equilibrio traslazionale, queste forze devono essere bilanciate. Ad esempio, se agisce una forza verticale diretta verso il basso, come il peso, deve esserci una forza verticale verso l'alto che ha esattamente la stessa grandezza.
Questa forza può essere fornita dalla mano che sostiene l'oggetto in modo che non cada, una corda o semplicemente la superficie di un tavolo.
Se c'è una forza tangenziale alla superficie, come l'attrito cinetico o statico, deve esserci un'altra forza opposta affinché esista l'equilibrio. Ad esempio, diamo un'occhiata al peso che pende dalle corde mostrato nella figura seguente.
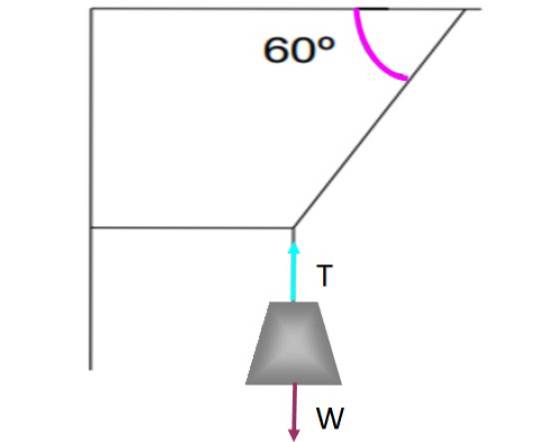
Il peso è mantenuto in equilibrio traslazionale e senza muoversi, grazie alla fune verticale che lo trattiene esercitando una tensione T che compensa il peso W. Ogni forza è stata rappresentata sul peso da una freccia, ciascuna di uguale dimensione e con la stessa direzione, ma in direzione opposta..
La forza di bilanciamento
Supponiamo che un insieme di forze agisca su un oggetto. Questo è chiamato a sistema di forza da cui la risultante può essere trovata come spiegato sopra: aggiungendo in modo vettoriale ciascuna delle forze del sistema.
Ebbene, si chiama la forza opposta a questa risultante forza di bilanciamento. Se la forza risultante è FR e la forza di bilanciamento è E, poi:
E + FR = 0
Perciò:
E = - FR
Esempi di equilibrio traslazionale
Molti oggetti che troviamo quotidianamente, dentro e fuori casa, sono in equilibrio traslazionale:
Edifici e strade
Gli edifici e le strade sono costruiti per rimanere stabili e non ribaltarsi o crollare. Tuttavia, nei grattacieli e in generale negli edifici molto alti, è necessaria una certa flessibilità per resistere all'azione del vento..
Libri e oggetti sugli scaffali
I libri in una biblioteca e i prodotti sugli scaffali dei negozi sono oggetti che rimangono in equilibrio traslazionale e non si muovono..
Il mobile
I mobili, la TV a schermo piatto e le immagini alle pareti, così come le lampade appese al soffitto, per citare alcuni oggetti, sono in equilibrio traslazionale..
Semafori
I semafori sono fissati da pali e cavi, in modo che non cadano. Eppure sappiamo che il vento li fa ondeggiare.
Illuminazione pubblica
Anche i lampioni sono in equilibrio traslazionale, fissati sui lampioni, come il lampione nell'immagine principale..
Esercizio risolto
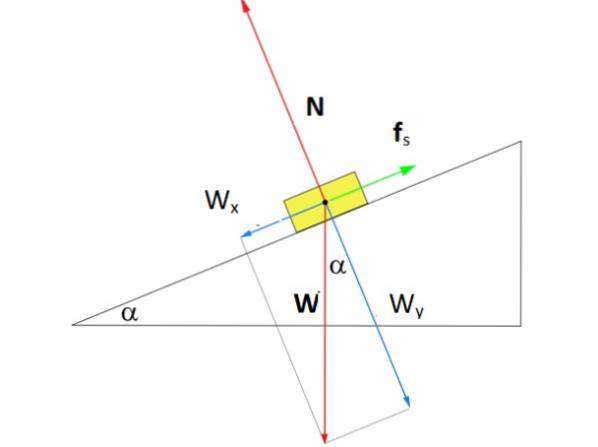
Quanto deve essere grande la forza FS di attrito statico in modo che la scatola in figura rimanga a riposo al centro del piano inclinato con un angolo α di 37º? La massa della scatola è m = 8 kg.
Soluzione
La figura mostra il diagramma a corpo libero della scatola sull'aereo. Ci sono tre forze che agiscono su di esso: il peso W, diretto verticalmente verso il basso, il normale N, che è la forza perpendicolare esercitata dalla superficie del piano sulla scatola, e infine la forza di attrito statico FS che si contrappone al box scorrevole in discesa.
La condizione di equilibrio traslazionale afferma che:
W + N + FS = 0
Bisogna però ricordare che questa è una somma vettoriale e per eseguirla è necessario scomporre le forze in componenti lungo gli assi delle coordinate.
Nella figura è stato disegnato un sistema di coordinate in cui l'asse x corre parallelo alla superficie del piano inclinato. Con questa scelta l'attrito statico cade su detto asse, mentre la normale è sull'asse y. Il peso è l'unica forza che è inclinata e deve essere scomposta con l'aiuto della trigonometria:
WX = W. sin α
WY = W. cos α
La somma delle forze lungo ogni asse è:
∑ FY = N - WY = 0
∑ FX = fS - WX = 0
Da quest'ultima equazione segue che:
FS = WX
E come WX = W. sin α e l'entità del peso a sua volta è W = m.g, dove g è il valore della gravità, quindi l'entità dell'attrito statico è semplicemente:
FS = m⋅g⋅sen α = 8 kg × 9,8 m / sDue × peccato 37º = 47,2 N.
Riferimenti
- Bauer, W. 2011. Fisica per l'ingegneria e le scienze. Volume 1. Mc Graw Hill.
- Figueroa, D. (2005). Serie: Fisica per la scienza e l'ingegneria. Volume 2. Dinamica. A cura di Douglas Figueroa (USB).
- Giambattista, A. 2010. Fisica. 2 °. Ed. McGraw Hill.
- Serway, R., Jewett, J. (2008). Fisica per la scienza e l'ingegneria. Volume 1. 7ma. Ed. Cengage Learning.
- Tippens, P. 2011. Fisica: concetti e applicazioni. 7a edizione. Mcgraw hill.



Nessun utente ha ancora commentato questo articolo.