Formula delle equazioni di secondo grado, come risolverle, esempi, esercizi

Il equazioni quadratiche o quadratiche e uno sconosciuto ha la forma ascia^Due + bx + c = 0. Dove a ≠ 0, poiché se fosse 0, l'equazione si trasformerebbe in un'equazione lineare, ei coefficienti a, bec sono numeri reali.

L'incognita da determinare è il valore di x. Ad esempio, l'equazione 3x^Due - 5x + 2 = 0 è un'equazione quadratica completa.

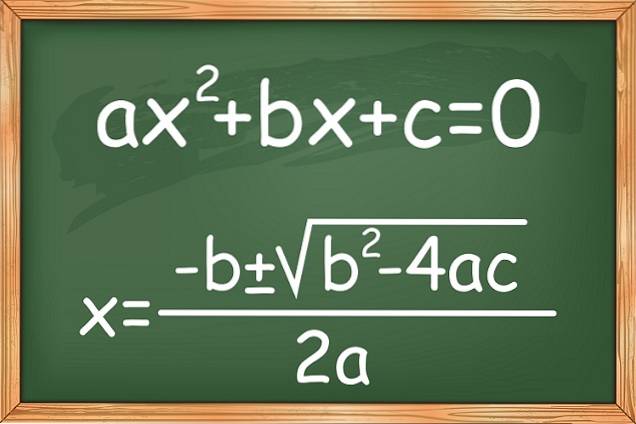
Esistono anche varianti note come equazioni di secondo grado incomplete, a cui mancano i termini, ad eccezione di quella di ascia^Due. Ecco alcuni esempi:

X^Due - 25 = 0

3x^Due - 5x = 0

Al Juarismi, il famoso matematico arabo dell'antichità, descrisse nelle sue opere vari tipi di equazioni di primo e secondo grado, ma solo con coefficienti positivi. Tuttavia, fu il matematico francese Francois Viete che per primo introdusse le lettere per simboleggiare le quantità e proporre la soluzione attraverso la formula risoluto:

Questa è una formula generale che permette di risolvere un'equazione quadratica, trovandone le radici o gli zeri, anche se le soluzioni non sono reali. Esistono anche altri modi per risolverli.

Indice articolo

• 1 Come risolvere le equazioni quadratiche?
  • 1.1 Risoluzione tramite factoring
  • 1.2 Metodo grafico
  • 1.3 Risoluzione con calcolatrice scientifica
  • 1.4 Discriminante di un'equazione quadratica
• 2 Esempi di semplici equazioni quadratiche
  • 2.1 Equazione della forma x2 + mx + n = 0
  • 2.2 Equazione incompleta della forma ax2 + c = 0
  • 2.3 Equazione incompleta della forma ax2 + bx = 0
  • 2.4 Equazioni con denominatore
  • 2.5 Equazioni di ordine superiore che diventano quadratiche
• 3 semplici esercizi risolti
  • 3.1 - Esercizio 1
  • 3.2 - Esercizio 2
  • 3.3 - Esercizio 3
• 4 Riferimenti

Come risolvere le equazioni quadratiche?

Le equazioni di secondo grado possono essere risolte con la formula data sopra, e ci sono anche altre procedure algebriche che possono dare risultato in alcune equazioni.

Risolveremo l'equazione proposta all'inizio con la formula, un metodo valido per qualsiasi equazione quadratica con uno sconosciuto:

3x^Due - 5x + 2 = 0

Per utilizzare correttamente la formula notiamo che:

• per è il coefficiente del termine con x^Due
• b è il coefficiente del termine lineare
• c è il termine indipendente.

Li identificheremo dalla stessa equazione:

a = 3

b = -5

c = 2

Si noti che il segno che accompagna il coefficiente deve essere preso in considerazione. Ora sostituiamo questi valori nella formula:

Al numeratore è presente il simbolo “più - meno” ±, che indica che la quantità con radice può essere considerata positiva e anche negativa. Un'equazione quadratica ha al massimo due soluzioni reali, e questo simbolo ne tiene conto.

Chiamiamo x₁ e x_Due a queste due soluzioni, quindi:

X₁ = (5 + 1) / 6 = 1

X_Due = (5-1) / 6 = 4/6 = 2/3

Risoluzione tramite factoring

Alcune equazioni di secondo grado sono costituite da trinomi facilmente fattorizzabili. In tal caso, questo metodo è molto più veloce. Consideriamo l'equazione:

X^Due + 7x - 18 = 0

La fattorizzazione ha questa forma:

(x +) ⋅ (x -)

Gli spazi vuoti sono riempiti con due numeri che moltiplicati danno 18 e quando sottratti danno 7. I segni tra parentesi sono scelti con questo criterio:

-Nella prima parentesi il segno è posto tra il primo e il secondo termine.

-E nella seconda parentesi c'è il prodotto dei segni che si vedono.

Per quanto riguarda i numeri, in questo caso sono facilmente valutabili: sono 9 e 2. Il più grande è sempre posto nella prima delle parentesi, in questo modo:

X^Due + 7x - 18 = (x + 9). (x - 2)

Il lettore può verificare tramite la proprietà distributiva, che sviluppando il prodotto del lato destro dell'uguaglianza si ottiene il trinomio del sinistro. Ora l'equazione viene riscritta:

(x + 9) ⋅ (x - 2) = 0

Perché l'uguaglianza sia soddisfatta, è sufficiente che uno dei due fattori sia zero. Quindi, nel primo devi fare x₁ = -9 o può essere che il secondo fattore svanisca, nel qual caso x_Due = 2. Queste sono le soluzioni dell'equazione.

Metodo grafico

Le radici o soluzioni dell'equazione quadratica corrispondono alle intersezioni della parabola y = ascia^Due + bx + c con l'asse orizzontale o l'asse x. Quindi, rappresentando graficamente la parabola corrispondente, troveremo la soluzione dell'equazione quadratica rendendo y = 0.

I tagli delle parabole con l'asse orizzontale rappresentano le soluzioni dell'equazione ascia^Due + bx + c = 0. Una parabola che taglia solo l'asse orizzontale in un unico punto ha un'unica radice e questo sarà sempre il vertice della parabola.

E infine, se una parabola non taglia l'asse orizzontale, l'equazione corrispondente ascia^Due + bx + c = 0 manca di soluzioni reali.

Costruire un grafico a mano può essere laborioso, ma con l'uso di programmi che rappresentano grafici online è molto semplice.

Risoluzione con calcolatrice scientifica

Molti modelli di calcolatrici scientifiche hanno la possibilità di risolvere equazioni quadratiche (e anche altri tipi di equazioni). Per scoprirlo, devi controllare il menu.

Una volta scelta l'equazione quadratica di un'opzione sconosciuta, il menu chiede di inserire i valori dei coefficienti a, bec e restituisce le soluzioni reali se esistono. E ci sono anche modelli di calcolatrici scientifiche che funzionano con numeri complessi e offrono queste soluzioni.

Discriminante di un'equazione quadratica

Per scoprire se l'equazione ha o meno soluzioni reali, e quante sono, senza dover prima risolverle, il discriminante Δ è definito come la quantità sotto la radice quadrata:

Δ = b^Due - 4ac

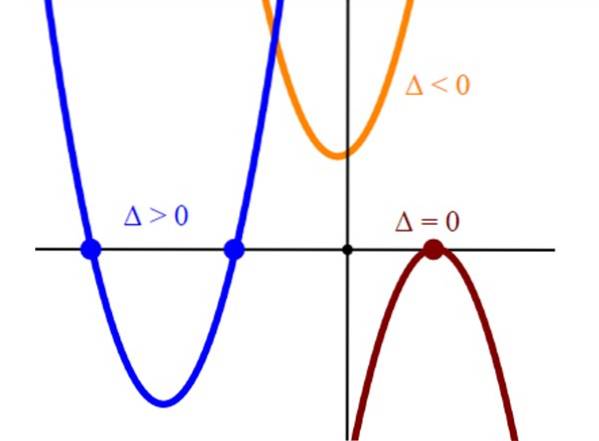
Secondo il segno del discriminante, si sa quante soluzioni ha l'equazione secondo questo criterio:

-Due soluzioni reali: Δ> 0

-Una soluzione reale (o due soluzioni identiche): Δ = 0

-Nessuna vera soluzione: Δ  < 0

Ad esempio, quante soluzioni fa l'equazione quadratica -7x^Due +12x + 64 = 0? Identifichiamo i coefficienti:

a = -7

b = 12

c = 64

Δ = b^Due - 4ac = 12^Due - 4x (-7) x 64 = 144 + 1792 = 1936> 0

L'equazione ha due soluzioni. Ora vediamo quest'altro:

X^Due - 6x + 9 = 0

a = 1

b = -6

c = 9

Δ = (-6)^Due - 4 x 1 x 9 = 36-36 = 0

Questa è un'equazione con una singola soluzione o con due soluzioni uguali.

Esempi di semplici equazioni quadratiche

All'inizio abbiamo detto che le equazioni di secondo grado potrebbero essere complete se il trinomio lo è, e incomplete se manca il termine lineare o il termine indipendente. Vediamo ora alcuni tipi particolari:

Equazione della forma x^Due + mx + n = 0

In questo caso a = 1 e la formula si riduce a:

Per questo tipo di equazione, e sempre a seconda dei coefficienti rimanenti, il metodo del factoring può funzionare bene, come abbiamo visto nella sezione precedente.

Equazione incompleta della forma ax^Due + c = 0

La soluzione, se esiste, è della forma:

C'è una soluzione reale quando a o c hanno un segno negativo, ma se i due termini hanno lo stesso segno, la soluzione sarà immaginaria.

Equazione incompleta della forma ax^Due + bx = 0

Questa equazione viene risolta rapidamente utilizzando il factoring, poiché x è un fattore comune in entrambi i termini. Una delle soluzioni è sempre x = 0, l'altra si trova così:

ascia^Due + bx = 0

x (ax + b) = 0

ax + b = 0 → x = -b / a

Vediamo un esempio di seguito. Organizzare:

X^Due - 5x = 0

x (x - 5) = 0

Pertanto x₁ = 0 e x_Due = 5

Equazioni con denominatore

Esistono varie equazioni di tipo razionale, in cui l'ignoto può essere presente sia al numeratore che al denominatore, o anche solo in quest'ultimo, e che mediante manipolazioni algebriche si riducono ad equazioni quadratiche.

Il modo per risolverli è moltiplicare entrambi i lati dell'uguaglianza per il minimo comune multiplo o m.c.m dei denominatori e quindi riorganizzare i termini. Per esempio:

Equazioni di ordine superiore che diventano quadratiche

Esistono equazioni di ordine superiore che possono essere risolte come se fossero quadratiche mediante un cambio di variabile, ad esempio questa equazione bi-quadrato:

X⁴ - 10x^Due + 9 = 0

Sia x^Due = u, allora l'equazione diventa:

o^Due - 10u + 9 = 0

Questa equazione viene risolta rapidamente fattorizzando, trovando due numeri che moltiplicati per 9 e sommati 10. Questi numeri sono 9 e 1:

(u - 9). (u - 1) = 0

Pertanto le soluzioni di questa equazione sono u₁ = 9 e u_Due = 1. Ora restituiamo la modifica:

X^Due = 9 → x₁ = 3 e x_Due = -3

X^Due = 1 → x₁ = 1 e x_Due = -1

L'equazione originale è di ordine 4, quindi ha almeno 4 radici. Quello nell'esempio è -3, -1, 1 e 3.

Semplici esercizi risolti

- Esercizio 1

Risolvi la seguente equazione quadratica con l'ignoto al denominatore:

Il minimo comune multiplo è x (x + 2) e devi moltiplicare tutti i termini:

L'espressione equivalente rimane:

5x (x + 2) - x = x (x + 2)

Sviluppiamo:

5x^Due + 10x - x = x^Due + 2x

Tutti i termini sono trasposti a sinistra dell'uguaglianza ea destra lasciamo 0:

5x^Due + 10x - x - x^Due - 2x = 0

4x^Due - 7x = 0

Consideriamo, poiché è un'equazione incompleta:

x (4x - 7) = 0

Una delle soluzioni è x = 0, l'altra è:

4x = 7

x = 7/4

- Esercizio 2

Trova la soluzione delle equazioni quadratiche:

a) -7x^Due +12x + 64 = 0

b) x^Due - 6x + 9 = 0

Soluzione a

Da questa equazione conosciamo il determinante Δ, perché prima era calcolato come esempio, quindi ne trarremo vantaggio, esprimendo la formula risolutiva in questo modo:

X₁ = (-12 + 44) / -14 = - (32/14) = - (16/7)

X_Due = (-12-44) / -14 = 4

Soluzione b

Il trinomio quadrato x^Due - 6x + 9 è fattorizzabile, poiché è un perfetto trinomio quadrato:

X^Due - 6x + 9 = (x-3)^Due = 0

La soluzione a questa equazione è x = 3.

- Esercizio 3

Qual è l'equazione le cui soluzioni sono 3 e 4?

Soluzione

L'espressione fattorizzata è:

(x - 3) ⋅ (x - 4) = 0

Applicazione della proprietà distributiva:

X^Due - 4x -3x + 12 = 0

I due termini centrali sono simili e possono essere ridotti, lasciando:

X^Due - 7x + 12 = 0

Riferimenti

1. Baldor. 1977. Algebra elementare. Edizioni culturali venezuelane.
2. Hoffman, J. Selezione di argomenti di matematica. Volume 2.
3. Jiménez, R. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Precalculus: Mathematics for Calculus. 5 °. Edizione. Cengage Learning.
5. Zapata, F. 4 modi per risolvere un'equazione quadratica. Estratto da: francesphysics.blogspot.com.
6. Zill, D. 1984. Algebra e trigonometria. Mcgraw hill.