Il equazioni di primo grado o lineari con uno sconosciuto sono quelli che possono essere espressi come la somma di due termini, come segue:
ax + b = 0
Dove a e b, con per ≠ 0, sono numeri reali R o anche complessi C.Per risolverlo, i termini vengono trasposti, il che significa cambiare i termini da una parte all'altra dell'uguaglianza.
Per risolvere l'ignoto viene trasposto il termine + b, che deve andare a destra dell'uguaglianza con segno cambiato.
ax = -b
Quindi il valore di x viene cancellato, in questo modo:
x = - b / a
Ad esempio, risolveremo la seguente equazione:
6x - 5 = 4
Trasponiamo il termine -5 a destra con un segno cambiato:
6x = 4 + 5
Ciò equivale ad aggiungere 5 a entrambi i lati dell'equazione originale:
6x - 5 + 5 = 4 + 5 → 6x = 9
E ora risolviamo la "x" sconosciuta:
x = 9/6 = 3/2
Che equivale a dividere entrambi i lati dell'uguaglianza per 6. Quindi possiamo usare quanto segue per ottenere la soluzione:
-La stessa quantità può essere aggiunta o sottratta da entrambi i lati dell'uguaglianza in un'equazione, senza alterarla.
-Puoi anche moltiplicare (o dividere) per la stessa quantità tutti i termini sia a sinistra che a destra dell'equazione.
-E se entrambi i membri di un'equazione vengono elevati allo stesso potere, neppure l'uguaglianza viene alterata.
Indice articolo
La soluzione di un'equazione di primo grado è anche nota come radice. È il valore di x che converte l'espressione originale in un'uguaglianza. Ad esempio in:
5x = 8x - 15
Se sostituiamo x = 5 in questa equazione, otteniamo:
5⋅5 = 8⋅5 - 15
25 = 40-15
25 = 25
Poiché le equazioni lineari di primo grado si presentano in molte forme, che a volte non sono ovvie, esistono una serie di regole generali che includono varie manipolazioni algebriche, al fine di trovare il valore dell'ignoto:
-Innanzitutto, se ci sono operazioni indicate, è opportuno eseguirle.
-I simboli di raggruppamento come parentesi, parentesi quadre e parentesi graffe, se presenti, devono essere rimossi mantenendo i segni appropriati.
-I termini sono trasposti per porre tutti quelli che contengono l'ignoto da una parte dell'uguaglianza e quelli che non lo contengono dall'altra.
-Quindi tutti i termini simili vengono ridotti per arrivare alla forma ax = -b.
-E l'ultimo passo è cancellare l'ignoto.
L'equazione di primo grado sollevata all'inizio può essere derivata dall'equazione della retta y = mx + c, rendendo y = 0. Il valore risultante di x corrisponde all'intersezione della retta con l'asse orizzontale.
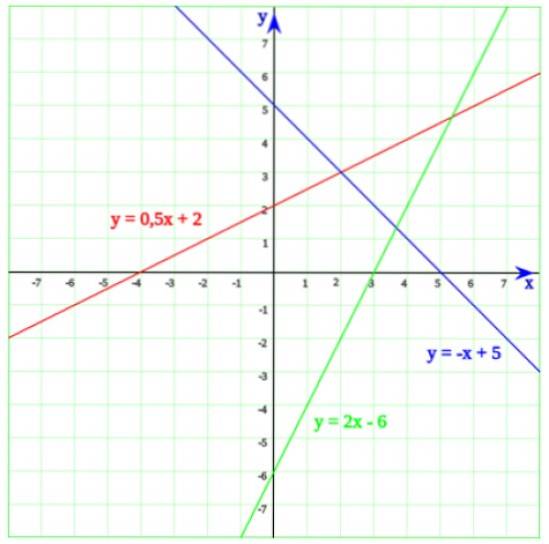
Nella figura seguente ci sono tre righe. A partire dalla linea verde, la cui equazione è:
y = 2x - 6
Rendendo y = 0 nell'equazione della retta si ottiene l'equazione di primo grado:
2x - 6 = 0
La cui soluzione è x = 6/2 = 3. Ora, quando dettagliamo il grafico, è facile rendersi conto che in effetti la linea interseca l'asse orizzontale in x = 3.
La linea blu interseca l'asse x in x = 5, che è la soluzione dell'equazione -x + 5 = 0. Infine, la linea la cui equazione è y = 0,5x + 2 interseca l'asse x in x = - 4 , che è facilmente visibile dall'equazione di primo grado:
0,5 x + 2 = 0
x = 2 / 0,5 = 4
Sono quelli nei cui termini non ci sono denominatori, ad esempio:
21 - 6x = 27 - 8x
La tua soluzione è:
-6x + 8x = 27-21
2x = 6
x = 3
Queste equazioni contengono almeno un denominatore diverso da 1. Per risolverle si consiglia di moltiplicare tutti i termini per il minimo comune multiplo (MCM) dei denominatori, in modo da eliminarli.
La seguente equazione è di tipo frazionario:
Poiché questi numeri sono piccoli, non è difficile vedere che m.c.m (6, 8,12) = 24. Questo risultato si ottiene facilmente esprimendo i numeri come prodotto dei numeri primi o delle loro potenze, vediamo:
6 = 3,2
8 = 23
12 = 2Due⋅3
Il minimo comune multiplo è determinato moltiplicando i fattori comuni e non comuni di 6, 8 e 12 con il loro massimo esponente, quindi:
mcm (6,8,12) = 23 ⋅3 = 8 × 3 = 24
Poiché abbiamo il minimo comune multiplo, deve essere moltiplicato per ciascuno dei termini dell'equazione:
4 (x + 5) -3 (2x + 3) = 2 (1-5x)
Facciamo uso della proprietà distributiva:
4x + 20 - 6x -9 = 2 - 10x
Tutti i termini che contengono la "x" sconosciuta sono raggruppati sul lato sinistro dell'uguaglianza, lasciando i termini indipendenti o numerici sul lato destro:
4x - 6x + 10 x = 2 +9-20
8x = -9
x = - 9/8
Sono equazioni lineari con uno sconosciuto, che però sono accompagnate da coefficienti letterali (lettere). Queste lettere vengono trattate allo stesso modo dei numeri. Un esempio di un'equazione letterale di primo grado è:
-3ax + 2a = 5x - b
Questa equazione viene risolta come se i termini e i coefficienti indipendenti fossero numerici:
-3ax - 5x = - b - 2a
Fattorizzazione della "x" sconosciuta:
x (-3a - 5) = - b - 2a
x = (- b - 2a) / (-3a - 5) → x = (2a + b) / (3a + 5)
I sistemi di equazioni sono costituiti da un insieme di equazioni con due o più incognite. La soluzione del sistema è costituita da valori che soddisfano le equazioni contemporaneamente e per determinarla inequivocabilmente, deve esserci un'equazione per ogni incognita.
La forma generale di un sistema di m equazioni lineari con n unknowns è:
perundiciX1 + per12XDue +… per1nXn = b1
perventunoX1 + per22XDue +… per2nXn = bDue
...
perm1X1 + perm2XDue +… permnXn = bm
Se il sistema ha una soluzione, si dice che sia compatibile determinato, quando c'è un insieme infinito di valori che lo soddisfano lo è compatibile indeterminato, e infine se non ha soluzione, allora lo è incompatibile.
Nella risoluzione di sistemi di equazioni lineari vengono utilizzati diversi metodi: riduzione, sostituzione, equalizzazione, metodi grafici, eliminazione di Gauss-Jordan e uso di determinanti sono tra i più utilizzati. Ma ci sono altri algoritmi per arrivare alla soluzione, più convenienti per sistemi con molte equazioni e incognite.
Un esempio di un sistema di equazioni lineari con due incognite è:
8x - 5 = 7y - 9
6x = 3y + 6
La soluzione di questo sistema è presentata più avanti nella sezione degli esercizi risolti..
Il valore assoluto di un numero reale è la distanza tra la sua posizione sulla linea numerica e 0 sulla linea numerica. Essendo una distanza, il suo valore è sempre positivo.
Il valore assoluto di un numero è indicato dalle barre modulo: │x│. Il valore assoluto di un numero positivo o negativo è sempre positivo, ad esempio:
│ + 8│ = 8
│-3│ = 3
In un'equazione di valore assoluto, l'incognita è tra le barre del modulo. Consideriamo la seguente semplice equazione:
│x│ = 10
Ci sono due possibilità, la prima è che x sia un numero positivo, nel qual caso abbiamo:
x = 10
E l'altra possibilità è che x sia un numero negativo, in questo caso:
x = -10
Queste sono le soluzioni di questa equazione. Ora diamo un'occhiata a un esempio diverso:
│x + 6│ = 11
L'importo all'interno delle barre può essere positivo, quindi:
x + 6 = 11
x = 11-6 = 5
Oppure può essere negativo. In quel caso:
-(x + 6) = 11
-x - 6 = 11 ⇒ -x = 11 + 6 = 17
E il valore dell'ignoto è:
x = -17
Questa equazione del valore assoluto ha quindi due soluzioni: x1 = 5 e xDue = -17. Possiamo verificare che entrambe le soluzioni portano a un'uguaglianza nell'equazione originale:
│5 + 6│ = 11
│11│ = 11
Y
│-17 + 6│ = 11
│-11│ = 11
Risolvi il seguente sistema di equazioni lineari con due incognite:
8x - 5 = 7y -9
6x = 3y + 6
Come viene proposto, questo sistema è ideale per utilizzare il metodo di sostituzione, poiché nella seconda equazione l'ignoto X è quasi pronto per l'autorizzazione:
x = (3y + 6) / 6
E può essere immediatamente sostituito nella prima equazione, che diventa quindi un'equazione di primo grado con "y" sconosciuta:
8 [(3 anni + 6) / 6] - 5 = 7 anni - 9
Il denominatore può essere rimosso moltiplicando ogni termine per 6:
6. 8⋅ [(3y + 6) / 6] - 6,5 = 6,7y- 6. 9
8⋅ (3 anni + 6) - 30 = 42 anni - 54
Applicando la proprietà distributiva nel primo termine al diritto di uguaglianza:
24 anni + 48-30 = 42 anni - 54 ⇒ 24 anni + 18 = 42 anni - 54
L'equazione può essere semplificata, poiché tutti i coefficienti sono multipli di 6:
4 anni + 3 = 7 anni - 9
-3y = -12
y = 4
Con questo risultato andiamo alla cancellazione di x:
x = (3y +6) / 6 → x = (12 + 6) / 6 = 3
Risolvi la seguente equazione:
I prodotti compaiono in questa equazione e, seguendo le istruzioni fornite all'inizio, devono essere prima sviluppati:
3x - 10x +14 = 5x + 36x + 12
Quindi tutti i termini che contengono le incognite vengono portati a sinistra dell'uguaglianza e a destra saranno i termini indipendenti:
3x - 10x - 5x - 36x = 12-14
-48x = -2
x = 1/24
Aggiungendo i tre angoli interni di un triangolo si ottengono 180º. La maggiore supera la minore di 35º, e quest'ultima a sua volta supera di 20º la differenza tra la maggiore e la media. Quali sono gli angoli?
Chiameremo "x" l'angolo maggiore, "y" quello centrale e "z" il più piccolo. Quando l'affermazione afferma che la loro somma è 180º, può essere scritta:
x + y + z = 180
Quindi sappiamo che il maggiore supera il minore di 35º, possiamo scrivere questo in questo modo:
x = z + 35
Infine, il più piccolo supera di 20º la differenza tra il più grande e il centro:
z = x - y + 20
Abbiamo un sistema di 3 equazioni e 3 incognite:
x + y + z = 180
x = z + 35
z = x - y + 20
Risolvendo per z dalla prima equazione abbiamo:
z = 180 - x - y
Abbinamento con il terzo:
180 - x - y = x - y + 20
Passando le incognite sul lato sinistro come sempre:
-x - y - x + y = 20-180
La "y" viene cancellata e rimane:
-2x = - 160
x = 80º
Dalla seconda equazione troviamo il valore di z:
z = x - 35 = 80 - 35 = 45º
E il valore di y si trova dal primo o dal terzo:
y = 180 - x - z = 180 - 80 - 45 = 55º
Nessun utente ha ancora commentato questo articolo.