Differenza tra una frazione comune e un numero decimale

Per identificare qual è la differenza tra una frazione comune e un numero decimale è sufficiente osservare entrambi gli elementi: uno rappresenta un numero razionale, e l'altro include nella sua costituzione una parte intera e una parte decimale.

Una “frazione comune” è l'espressione di una quantità divisa per un'altra, senza effettuare detta divisione. Matematicamente, una frazione comune è un numero razionale, che è definito come il quoziente di due numeri interi "a / b", dove b ≠ 0.

Un "numero decimale" è un numero composto da due parti: una parte intera e una parte decimale..

Per separare la parte intera dalla parte decimale, viene inserita una virgola, chiamata punto decimale, sebbene venga utilizzato anche un punto a seconda della bibliografia.

Numeri decimali

Un numero decimale può avere un numero finito o infinito di numeri nella sua parte decimale. Inoltre, il numero infinito di cifre decimali può essere scomposto in due tipi:

Periodico

Cioè, ha uno schema ripetitivo. Ad esempio, 2.454545454545…

Non periodico

Non hanno schemi ripetitivi. Ad esempio, 1.7845265397219…

I numeri che hanno un numero periodico infinito o infinito di cifre decimali sono chiamati numeri razionali, mentre quelli che hanno un numero infinito non periodico sono chiamati irrazionali.

L'unione dell'insieme dei numeri razionali e dell'insieme dei numeri irrazionali è nota come l'insieme dei numeri reali.

Differenze tra frazione comune e numero decimale

Le differenze tra una frazione comune e un numero decimale sono:

1- Parte decimale

Ogni frazione comune ha un numero finito di numeri nella sua parte decimale o un numero periodico infinito, mentre un numero decimale può avere un numero infinito non periodico di numeri nella sua parte decimale..

Quanto sopra dice che ogni numero razionale (ogni frazione comune) è un numero decimale, ma non ogni numero decimale è un numero razionale (una frazione comune).

2- Notazione

Ogni frazione comune è indicata come il quoziente di due numeri interi, mentre un numero decimale irrazionale non può essere indicato in questo modo..

I numeri decimali irrazionali più utilizzati in matematica sono indicati con radici quadrate (√ ), cubico (³√ ) e gradi superiori.

Oltre a questi, ci sono due numeri molto famosi, che sono il numero di Eulero, indicato con e; e il numero pi greco, indicato con π.

Come passare da una frazione comune a un numero decimale?

Per passare da una frazione comune a un numero decimale, basta fare la divisione corrispondente. Ad esempio, se hai 3/4, il numero decimale corrispondente è 0,75.

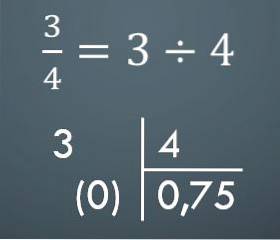
Come passare da un numero decimale razionale a una frazione comune?

È anche possibile eseguire il processo inverso a quello precedente. L'esempio seguente illustra una tecnica per passare da un numero decimale razionale a una frazione comune:

- Sia x = 1,78

Poiché x ha due cifre decimali, l'uguaglianza precedente viene moltiplicata per 10² = 100, con la quale si ottiene 100x = 178; e risolvendo per x risulta che x = 178/100. Quest'ultima espressione è la frazione comune che rappresenta il numero 1,78.

Ma questo processo può essere fatto per numeri con un numero infinito periodico di cifre decimali? La risposta è sì e il seguente esempio mostra i passaggi da seguire:

- Sia x = 2,193193193193 ...

Poiché il periodo di questo numero decimale ha 3 cifre (193), l'espressione precedente viene moltiplicata per 10³ = 1000, con la quale si ottiene l'espressione 1000x = 2193.193193193193 ... .

Ora l'ultima espressione viene sottratta dalla prima e l'intera parte decimale viene cancellata, lasciando l'espressione 999x = 2191, da cui si ricava che la frazione comune è x = 2191/999.

Riferimenti

1. Anderson, J. G. (1983). Matematica del negozio tecnico (Illustrato ed.). Industrial Press Inc.
2. Avendaño, J. (1884). Manuale completo di istruzione elementare e primaria superiore: ad uso di aspiranti insegnanti e soprattutto studenti delle Scuole Normali della Provincia (2 ed., Vol. 1). Stampa di D. Dionisio Hidalgo.
3. Coates, G. e. (1833). L'aritmetica argentina: trattato completo sull'aritmetica pratica. Ad uso delle scuole. Stampa dello Stato.
4. Dal mare. (1962). Matematica per il seminario. Reverte.
5. DeVore, R. (2004). Problemi pratici in matematica per i tecnici del riscaldamento e del raffreddamento (Illustrato ed.). Cengage Learning.
6. Jariez, J. (1859). Corso completo di scienze matematiche fisiche e meccaniche applicate alle arti industriali (2 ed.). Tipografia ferroviaria.
7. Palmer, C. I., & Bibb, S. F. (1979). Matematica pratica: aritmetica, algebra, geometria, trigonometria e regolo calcolatore (ristampa ed.). Reverte.