Il densità apparente di un campione è definito come il quoziente tra la sua massa e il volume inalterato, che comprende tutti gli spazi o pori che contiene. Se c'è aria in questi spazi, la densità apparente ρb, o densità apparente è:
ρb = Massa / volume = massa particelle + Massa aria /Volume particelle+ Volume aria
Quando si calcola la densità apparente di un campione di terreno, deve essere preventivamente essiccato in un forno a 105 ºC fino a quando la massa è costante, indicando che tutta l'aria è evaporata..
Secondo questa definizione, la densità apparente dei suoli o densità secca, si calcola in questo modo:
ρS = Peso degli elementi solidi / Volume solido + Volume pori
Indicare come MS a peso secco o massa e Vt = VS + Vp come volume totale, la formula è:
ρS = MS / Vt
Indice articolo
Le unità di densità apparente nel Sistema internazionale di unità sono kg / m3. Tuttavia, altre unità come g / cm3 e megagrammi / metro cubo: Mg / m3 sono anche ampiamente utilizzati.
Il concetto di densità apparente è molto utile quando si tratta di materiali eterogenei e porosi come i terreni, poiché è indicativo della loro capacità di drenaggio e aerazione, tra le altre qualità..
Ad esempio, i terreni a bassa porosità hanno densità apparenti elevate, sono compatti e tendono ad allagarsi facilmente, a differenza dei terreni porosi..
Quando c'è acqua o un altro fluido nei pori del campione, il volume dopo l'essiccazione diminuisce, quindi, quando si effettuano i calcoli, è necessario conoscere la proporzione d'acqua originale (vedi esempio risolto).
La densità apparente dei materiali in generale, compreso il suolo, è molto variabile, poiché vi sono fattori come il grado di compattazione, la presenza di materia organica, la sua consistenza, struttura, profondità e altri, che ne influenzano la forma e la forma. degli spazi dei pori.
I suoli sono definiti come una miscela eterogenea di sostanze inorganiche, sostanze organiche, aria e acqua. Al tatto possono essere struttura fine, media o grossolana, mentre le particelle componenti possono essere disposte in vari modi, un parametro noto come struttura.
Suoli fini, ben strutturati con un'alta percentuale di sostanza organica tendono ad avere valori bassi di densità apparente. Al contrario, i terreni spessi, con meno materia organica e poca struttura, tendono ad avere valori più alti.
In base alla sua consistenza, la densità apparente ha i seguenti valori:
| Struttura | Densità apparente (g / cm3) |
|---|---|
| Bene | 1.00 - 1.30 |
| Mediano | 1,30 - 1,50 |
| Schifoso | 1,50 - 1,70 |
Questi valori servono come riferimento generale. In terreni torbosi, abbondanti di residui vegetali, la densità apparente può arrivare fino a 0,25 g / cm3, se è un terreno minerale vulcanico è intorno a 0,85 g / cm3, mentre in terreni molto compatti raggiunge 1,90 g / cm3.
Il valore della densità apparente aumenta anche con la profondità, poiché il terreno è generalmente più compattato e ha una percentuale inferiore di materia organica..
L'interno del terreno è composto da strati o strati orizzontali, chiamati orizzonti. Gli orizzonti hanno diverse trame, composizione e compattazione. Pertanto presentano variazioni in termini di densità apparente.
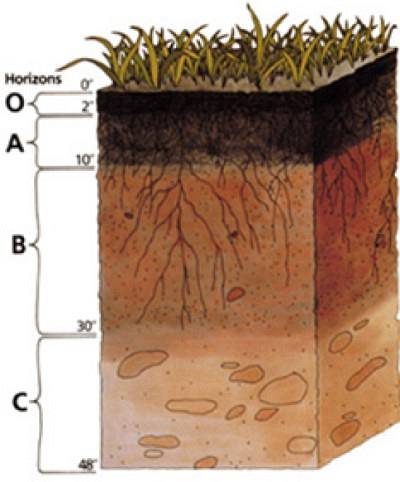
Uno studio del suolo si basa su di esso profilo, che consiste di vari orizzonti che si verificano in modo verticale ordinato.
Poiché la variabilità della densità apparente è molto ampia, spesso deve essere misurata direttamente con varie procedure..
Il metodo più semplice è quello di estrarre un campione dal terreno, inserendovi un trapano con un cilindro metallico spaziale di volume noto e facendo attenzione a non compattare il terreno. Il campione estratto viene sigillato, per evitare perdite di umidità o alterazioni delle caratteristiche.
Quindi in laboratorio il campione viene estratto, pesato e quindi posto in una stufa a 105 ° C per essiccare per 24 ore..
Sebbene sia il modo più semplice per trovare la densità secca del terreno, non è il più consigliato per terreni con tessiture molto sciolte o pieni di pietre..
Per questi è preferibile il metodo di scavare una buca e salvare la terra estratta, che sarà il campione da essiccare. Il volume del campione viene determinato versando sabbia asciutta o acqua nel foro scavato.
In ogni caso dal campione è possibile determinare proprietà molto interessanti del terreno per caratterizzarlo. Il seguente esercizio risolto descrive come farlo.
Dal cilindro del campione viene prelevato un campione di argilla della lunghezza di 100 mm, il cui diametro interno è anch'esso di 100 mm. Alla pesata si è ottenuta una massa di 1531 g, che una volta essiccata è stata ridotta a 1178 g. Il peso specifico delle particelle è 2,75. Viene chiesto di calcolare:
a) La densità apparente del campione
b) Contenuto di umidità
c) Il rapporto dei vuoti
d) Densità a secco
e) Il grado di saturazione
f) Contenuto d'aria
Il volume senza alterare Vt è il volume originale del campione. Per un cilindro di diametro D e altezza h, il volume è:
V cilindro = Vt = Area della base x altezza = πDDue/ 4 = π x (100 x 10-3 m)Due x 100 x 10 -3 m / 4 = 0,000785 m3
L'affermazione afferma che la massa del campione è MS = 1531 g, quindi secondo l'equazione data all'inizio:
ρb = MS / Vt = 1531 g / 0,000785 m3 = 1950319 g / m3 = 1,95 Mg / m3
Poiché abbiamo la massa originale e la massa secca, la massa dell'acqua contenuta nel campione è la differenza di queste due:
M acqua = 1531 g - 1178 g = 353 g
La percentuale di umidità nel campione viene calcolata come segue:
% Umidità = (Mass acqua / Ms) x 100% = (353 g / 1178 g) = 29,97%
Per trovare il rapporto dei vuoti, è necessario scomporre il volume totale del campione Vt sopra:
V t = V particelle + Volume pori
Il volume occupato dalle particelle si ricava dalla massa secca e dal peso specifico, dati ottenuti dalla dichiarazione. Il peso specifico sg è il quoziente tra la densità del materiale e la densità dell'acqua in condizioni standard, quindi la densità del materiale è:
ρ = sg x ρacqua = 2,75 x 1 g / cm3 = 2,75 g / cm3
ρ = MS / VS → VS = 1,178 g / 2,75 g / cm3 = 0,428 cm3 = 0.000428 m3
Il volume dei vuoti nel campione è Vv = Vt - VS = 0.000785 m3 - 0.000428 m3 = 0.000357 m3.
Il rapporto dei vuoti e è:
e = Vv / VS = 0.000357 m3 / 0.000428 m3 = 0,83
La densità a secco del campione si calcola come indicato in premessa:
ρS = Peso degli elementi solidi / Volume solido + Volume pori= 1178 g / 0,000785 m3 = 1,5 Mg / m3
Il grado di saturazione è S = (Vacqua / Vv ) x 100%. Poiché conosciamo la massa d'acqua nel campione, calcolata al punto b) e la sua densità, il calcolo del suo volume è immediato:
ρacqua = Macqua / V acqua → Vacqua = 353 g / 1 g / cm3 = 353 cm3 = 0.000353 m3
D'altra parte, il volume dei vuoti è stato calcolato al punto c)
S = (0.000353 m3 / 0.000357 m3) x 100% = 98,9%
Infine la percentuale di contenuto d'aria è A = (Varia / Vt) x 100%. Il volume d'aria corrisponde a:
Vv - Vacqua = 0.000357 m3 - 0.000353 m3 = 0,000004 m3
A = (Varia / Vt) x 100% = (0,000004 m3/ 0.000785 m3) x100% = 0,51%
Nessun utente ha ancora commentato questo articolo.