Esempi di dati raggruppati ed esercizio risolto

Il dati raggruppati sono quelli che sono stati classificati in categorie o classi, prendendo come criterio la loro frequenza. Questo viene fatto per semplificare la gestione di grandi quantità di dati e stabilirne le tendenze..

Una volta organizzati in queste classi in base alle loro frequenze, i dati costituiscono un file distribuzione di frequenza, da cui si estraggono informazioni utili attraverso le sue caratteristiche.

Ecco un semplice esempio di dati raggruppati:

Supponiamo di misurare l'altezza di 100 studentesse, selezionate tra tutti i corsi di fisica di base di un'università, e di ottenere i seguenti risultati:

I risultati ottenuti sono stati suddivisi in 5 classi, che compaiono nella colonna di sinistra.

La prima classe, tra 155 e 159 cm, ha 6 studenti, la seconda classe 160 - 164 cm ha 14 studenti, la terza classe da 165 a 169 cm ha il maggior numero di membri: 47. Poi la classe continua 170-174 cm con 28 studenti e infine il 175-174 cm con solo 5.

Il numero di membri di ogni classe è precisamente il frequenza o Assoluta frequenza e aggiungendoli tutti, si ottiene il totale dei dati, che in questo esempio è 100.

Indice articolo

• 1 Caratteristiche della distribuzione di frequenza
  • 1.1 Frequenza
  • 1.2 Limiti
  • 1.3 Confini
  • 1.4 Ampiezza
  • 1.5 Marchio di classe
• 2 Misure di tendenza centrale e dispersione per dati raggruppati
  • 2.1 Media
  • 2.2 Mediana
  • 2.3 Moda
  • 2.4 Varianza e deviazione standard
• 3 Esercizio risolto
  • 3.1 Soluzione a
  • 3.2 Soluzione b
  • 3.3 Soluzione d
• 4 Riferimenti

Caratteristiche della distribuzione di frequenza

Frequenza

Come abbiamo visto, la frequenza è il numero di volte in cui un dato viene ripetuto. E per facilitare i calcoli delle proprietà della distribuzione, come la media e la varianza, vengono definite le seguenti quantità:

-Frequenza cumulativa: si ottiene sommando la frequenza di una classe con la precedente frequenza accumulata. La prima di tutte le frequenze corrisponde a quella dell'intervallo in questione e l'ultima è il numero totale di dati.

-Frequenza relativa: calcolato dividendo la frequenza assoluta di ciascuna classe per il numero totale di dati. E se moltiplichi per 100 hai la frequenza percentuale relativa.

-Frequenza relativa cumulativa: è la somma delle frequenze relative di ciascuna classe con le precedenti accumulate. L'ultima delle frequenze relative accumulate deve essere uguale a 1.

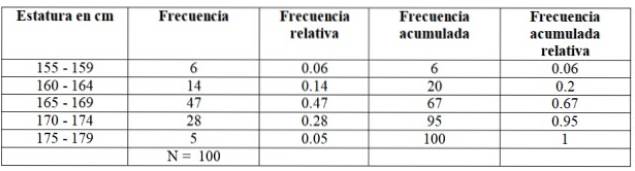
Per il nostro esempio, le frequenze hanno questo aspetto:

Limiti

Vengono chiamati i valori estremi di ogni classe o intervallo limiti di classe. Come possiamo vedere, ogni classe ha un limite inferiore e uno superiore. Ad esempio, la prima classe nello studio sulle altezze ha un limite inferiore di 155 cm e un limite superiore di 159 cm..

Questo esempio ha limiti chiaramente definiti, tuttavia è possibile definire limiti aperti: se invece di definire i valori esatti, dì "altezza inferiore a 160 cm", "altezza inferiore a 165 cm" e così via.

frontiere

L'altezza è una variabile continua, quindi si può considerare che la prima classe inizia effettivamente da 154,5 cm, poiché arrotondando questo valore all'intero più vicino si ottengono 155 cm.

Questa classe copre tutti i valori fino a 159,5 cm, perché dopo questo le altezze vengono arrotondate a 160,0 cm. Un'altezza di 159,7 cm appartiene già alla seguente classe.

I limiti di classe effettivi per questo esempio sono, in cm:

• 154,5 - 159,5
• 159,5 - 164,5
• 164,5 - 169,5
• 169,5 - 174,5
• 174,5 - 179,5

Ampiezza

La larghezza di una classe si ottiene sottraendo i confini. Per il primo intervallo del nostro esempio abbiamo 159,5 - 154,5 cm = 5 cm.

Il lettore può verificare che anche per gli altri intervalli dell'esempio l'ampiezza è di 5 cm. Tuttavia, va notato che le distribuzioni possono essere costruite con intervalli di ampiezza diversa.

Marchio di classe

È il punto medio dell'intervallo ed è ottenuto dalla media tra il limite superiore e il limite inferiore.

Per il nostro esempio, il voto della prima classe è (155 + 159) / 2 = 157 cm. Il lettore può vedere che i voti di classe rimanenti sono: 162, 167, 172 e 177 cm.

Determinare i voti di classe è importante, poiché sono necessari per trovare la media aritmetica e la varianza della distribuzione.

Misure di tendenza centrale e dispersione per dati aggregati

Le misure di tendenza centrale più comunemente utilizzate sono la media, la mediana e il modo, e descrivono con precisione la tendenza dei dati a raggrupparsi attorno a un certo valore centrale..

Metà

È una delle principali misure di tendenza centrale. Nei dati raggruppati, la media aritmetica può essere calcolata utilizzando la formula:

-X è la media

-F_io è la frequenza della lezione

-m_io è il segno di classe

-g è il numero di classi

-n è il numero totale di dati

Mediano

Per la mediana è necessario identificare l'intervallo in cui si trova l'osservazione n / 2. Nel nostro esempio, questa osservazione è il numero 50, perché ci sono un totale di 100 punti dati. Questa osservazione è compresa tra 165-169 cm.

Quindi devi interpolare per trovare il valore numerico che corrisponde a quell'osservazione, per la quale viene utilizzata la formula:

Dove:

-c = larghezza dell'intervallo in cui si trova la mediana

-B_M = il limite inferiore dell'intervallo a cui appartiene la mediana

-F_m = numero di osservazioni contenute nell'intervallo mediano

-n / 2 = metà dei dati totali

-F_BM = numero totale di osservazioni prima intervallo mediano

moda

Per la modalità viene identificata la classe modale, quella che contiene il maggior numero di osservazioni, di cui si conosce il marchio di classe.

Varianza e deviazione standard

La varianza e la deviazione standard sono misure di dispersione. Se indichiamo la varianza con s^Due e la deviazione standard, che è la radice quadrata della varianza come s, per i dati raggruppati avremo rispettivamente:

Y

Esercizio risolto

Per la distribuzione delle altezze delle studentesse universitarie proposte all'inizio, calcolare i valori di:

a) Media

b) Mediana

c) Moda

d) Varianza e deviazione standard.

Soluzione a

Costruiamo la seguente tabella per facilitare i calcoli:

Sostituzione di valori ed esecuzione diretta della somma:

X = (6 x 157 + 14 x 162 + 47 x 167 + 28 x 172+ 5 x 177) / 100 cm =

= 167,6 cm

Soluzione b

L'intervallo a cui appartiene la mediana è di 165-169 cm perché è l'intervallo con la frequenza più alta.

Identifichiamo ciascuno di questi valori nell'esempio, con l'aiuto della Tabella 2:

c = 5 cm (vedere la sezione ampiezza)

B_M = 164,5 cm

F_m = 47

n / 2 = 100/2 = 50

F_BM = 20

Sostituendo nella formula:

L'intervallo che contiene la maggior parte delle osservazioni è di 165-169 cm, il cui voto di classe è di 167 cm.

Soluzione d

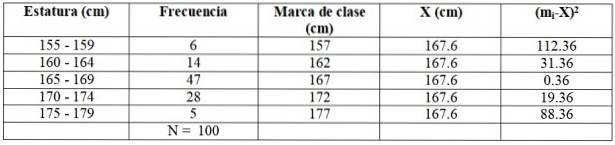
Espandiamo la tabella precedente aggiungendo due colonne aggiuntive:

Applichiamo la formula:

E sviluppiamo la sommatoria:

S^Due = (6 x 112,36 + 14 x 31,36 + 47 x 0,36 + 28 x 19,36 + 5 x 88,36) / 99 = = 21,35 cm^Due

Perciò:

s = √21,35 cm^Due = 4,6 cm

Riferimenti

1. Berenson, M. 1985. Statistiche per la gestione e l'economia. Interamericana S.A.
2. Canavos, G. 1988. Probabilità e statistica: applicazioni e metodi. Mcgraw hill.
3. Devore, J. 2012. Probabilità e statistica per l'ingegneria e la scienza. 8 °. Edizione. Cengage.
4. Levin, R. 1988. Statistics for Administrators. 2 °. Edizione. Prentice Hall.
5. Spiegel, M. 2009. Statistiche. Serie Schaum. 4 ° Edizione. Mcgraw hill.
6. Walpole, R. 2007. Probabilità e statistica per l'ingegneria e le scienze. Pearson.