
Compressibilità di solidi, liquidi, gas, esempi
Il comprimibilità di una sostanza o di un materiale è il cambiamento di volume che subisce quando è sottoposto a un cambiamento di pressione. In generale, il volume diminuisce quando la pressione viene applicata a un sistema o un oggetto. Tuttavia, a volte accade il contrario: un cambiamento di pressione può produrre un'esplosione in cui il sistema aumenta di volume, o quando si verifica un cambiamento di fase..
In alcune reazioni chimiche questo può accadere e anche nei gas, poiché all'aumentare della frequenza delle collisioni si generano le forze repulsive..

Quando immagini quanto possa essere facile o difficile comprimere un oggetto, considera i tre stati in cui si trova normalmente la materia: solido, liquido e gas. In ciascuna di esse le molecole mantengono determinate distanze l'una dall'altra. Più forti sono i legami che uniscono le molecole della sostanza che compongono l'oggetto e più sono vicini, più difficile sarà provocare una deformazione.
Un solido ha le sue molecole molto vicine tra loro e quando si cerca di avvicinarle tra loro, compaiono forze repulsive che rendono difficile il compito. Pertanto si dice che i solidi non siano molto comprimibili. Nelle molecole dei liquidi c'è più spazio, quindi la loro compressibilità è maggiore, ma anche così la variazione di volume richiede solitamente grandi forze.
Quindi solidi e liquidi sono difficilmente comprimibili. Sarebbe necessaria una variazione di pressione molto ampia per ottenere una variazione di volume apprezzabile nelle cosiddette condizioni normali di pressione e temperatura. D'altra parte, i gas, poiché le loro molecole sono ampiamente distanziate, sono facilmente compressi e decompressi.
Indice articolo
- 1 Comprimibilità dei solidi
- 1.1 -Compressibilità di un materiale
- 2 Esercizi-esempi risolti
- 2.1 -Esercizio risolto 1
- 2.2 -Esercizio risolto 2
- 2.3 -Esercizio risolto 3
- 3 Compressibilità nei gas
- 3.1 -Esercizio risolto 5
- 4 Riferimenti
Comprimibilità solida
Quando un oggetto è immerso in un fluido, ad esempio, esercita una pressione sull'oggetto in tutte le direzioni. In questo modo possiamo pensare che il volume dell'oggetto diminuirà, anche se nella maggior parte dei casi questo non sarà apprezzabile..
La situazione può essere vista nella figura seguente:
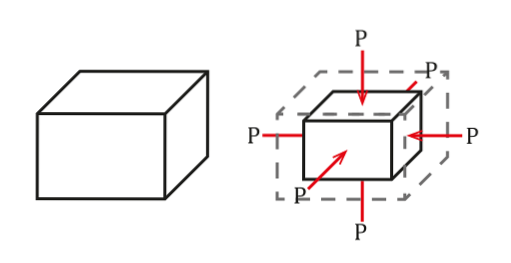
La pressione è definita come forza per unità di area, che provocherà una variazione di volume ΔV proporzionale al volume iniziale dell'oggetto Vo. Questa variazione di volume dipenderà dalle sue qualità..
La legge di Hooke afferma che la deformazione subita da un oggetto è proporzionale allo stress applicato ad esso:
Stress ∝ Strain
La deformazione volumetrica subita da un corpo è quantificata da B la costante di proporzionalità richiesta, chiamata modulo volumetrico del materiale:
B = -Stress / Strain
B = -ΔP / (ΔV / Vo)
Come ΔV / Vo è una quantità adimensionale, poiché è il quoziente tra due volumi, il modulo volumetrico ha le stesse unità di pressione, che nel Sistema Internazionale sono Pascal (Pa).
Il segno negativo indica la riduzione di volume prevista, quando l'oggetto è sufficientemente compresso, cioè la pressione aumenta.
-Comprimibilità di un materiale
Il valore inverso o reciproco del modulo volumetrico è noto come comprimibilità ed è indicato dalla lettera K. Perciò:

Qui K è il negativo della variazione frazionaria del volume per aumento della pressione. Le sue unità nel Sistema Internazionale sono gli inversi di Pa, cioè mDue / N.
L'equazione per B o per k se preferisci, è applicabile sia ai solidi che ai liquidi. Il concetto di modulo volumetrico è raramente applicato ai gas. Di seguito viene spiegato un semplice modello per quantificare la diminuzione del volume che un gas reale può subire..
La velocità del suono e il modulo di compressibilità
Un'applicazione interessante è la velocità del suono in un mezzo, che dipende dal suo modulo di compressibilità:

Esercizi-esempi risolti
-Risolto esercizio 1
Una sfera in ottone massiccio il cui volume è di 0,8 m3 viene lasciato cadere nell'oceano a una profondità in cui la pressione idrostatica è di 20 M Pa maggiore rispetto alla superficie. Come cambierà il volume della sfera? È noto che il modulo di compressibilità dell'ottone è B = 35.000 MPa,
Soluzione
1 M Pa = 1 Mega pascal = 1. 10 6 papà
La variazione di pressione rispetto alla superficie è DP = 20 x 10 6 Pa. Applicando l'equazione data per B, abbiamo:
B = -ΔP / (ΔV / Vo)
Perciò:

ΔV = -5,71,10 -4 x 0,8 m3 = -4,57 x 10-4 m3
La differenza di volume può avere segno negativo quando il volume finale è inferiore al volume iniziale, quindi questo risultato concorda con tutte le ipotesi fatte finora.
L'elevatissimo modulo di compressibilità indica che è necessaria una grande variazione di pressione affinché l'oggetto subisca un'apprezzabile diminuzione di volume..
-Esercizio risolto 2
Mettendo l'orecchio contro i binari della ferrovia, puoi dire quando uno di questi veicoli si sta avvicinando in lontananza. Quanto tempo impiega il suono quando si viaggia su una rotaia d'acciaio se il treno è a 1 km di distanza?
Dati
Densità dell'acciaio = 7,8 x 10 3 kg / m3
Modulo di compressibilità dell'acciaio = 2,0 x 10 undici papà.
Soluzione

Il modulo di compressibilità B calcolato sopra si applica anche ai liquidi, sebbene generalmente sia richiesto un grande sforzo per produrre un'apprezzabile diminuzione di volume. Ma i fluidi possono espandersi o contrarsi quando si riscaldano o si raffreddano, e ugualmente se sono depressurizzati o pressurizzati..
Per l'acqua in condizioni standard di pressione e temperatura (0 ° C e una pressione atmosferica circa o 100 kPa), il modulo volumetrico è di 2100 MPa. Cioè, circa 21.000 volte la pressione atmosferica.
Per questo motivo, nella maggior parte delle applicazioni, i liquidi sono generalmente considerati incomprimibili. Questo può essere verificato immediatamente con l'applicazione numerica.
-Esercizio risolto 3
Trova la diminuzione frazionaria del volume dell'acqua quando è sottoposta a una pressione di 15 MPa.
Soluzione

Comprimibilità nei gas
I gas, come spiegato sopra, funzionano in modo leggermente diverso.
Per sapere che volume hanno n moli di un dato gas se mantenute confinate a pressione P ea una temperatura T, viene utilizzata l'equazione di stato. Nell'equazione di stato per un gas ideale, in cui le forze intermolecolari non vengono prese in considerazione, il modello più semplice afferma che:
P.Videale = n. R. T
Dove R è la costante del gas ideale.
Le variazioni del volume del gas possono essere eseguite a pressione costante o temperatura costante. Ad esempio, mantenendo costante la temperatura, la compressibilità isotermica ΚT è:

Al posto del simbolo "delta" che era usato in precedenza per definire il concetto di solidi, per un gas viene descritto con una derivata, in questo caso derivata parziale rispetto a P, mantenendo T costante.
Perciò BT il modulo di compressibilità isotermico è:

E anche il modulo di compressibilità adiabatico B è importante.adiabatico, per cui non c'è flusso di calore in entrata o in uscita.
Badiabatico = γp
Dove γ è il coefficiente adiabatico. Con questo coefficiente si può calcolare la velocità del suono nell'aria:

Applicando l'equazione di cui sopra, trova la velocità del suono nell'aria.
Dati
Il modulo di compressibilità adiabatica dell'aria è 1,42 × 105 papà
La densità dell'aria è di 1.225 kg / m3 (a pressione atmosferica e 15 ºC)
Soluzione

Invece di lavorare con il modulo di compressibilità, come variazione unitaria di volume per variazione di pressione, il fattore di compressibilità di un gas reale, un concetto diverso ma illustrativo di come il gas reale si confronta con il gas ideale:
P. Vvero = Z. R. T
Dove Z è il coefficiente di compressibilità del gas, che dipende dalle condizioni in cui si trova, essendo generalmente funzione sia della pressione P che della temperatura T, e può essere espresso come:
Z = f (P, T)
Nel caso di un gas ideale Z = 1. Per i gas reali il valore Z quasi sempre aumenta con la pressione e diminuisce con la temperatura.
All'aumentare della pressione, le molecole gassose entrano in collisione più frequentemente e le forze repulsive tra di loro aumentano. Ciò può portare ad un aumento del volume nel gas reale, per cui Z> 1.
Al contrario, a pressioni inferiori, le molecole sono libere di muoversi e predominano le forze attrattive. In tal caso, Z < 1.
Per il caso semplice di 1 mole di gas n = 1, se vengono mantenute le stesse condizioni di pressione e temperatura, dividendo le precedenti equazioni termine per termine, si ottiene:

Vvero = Z Videale
-Esercizio risolto 5
Esiste un gas reale a 250 ºK e 15 atm di pressione, che ha un volume molare inferiore del 12% rispetto a quello calcolato dall'equazione di stato del gas ideale. Se la pressione e la temperatura vengono mantenute costanti, trova:
a) Il fattore di compressibilità.
b) Il volume molare del gas reale.
c) Che tipo di forze predominano: attrattive o repulsive?
Soluzione
a) Se il volume reale è del 12% inferiore a quello ideale, significa che:
Vvero = 0,88 Videale
Pertanto per 1 mole di gas, il fattore di compressibilità è:
Z = 0,88
b) Scelta della costante del gas ideale con le unità appropriate per i dati forniti:
R = 0,082 l. Atm / mol. K.
Il volume molare viene calcolato risolvendo e sostituendo i valori:
c) Le forze attrattive predominano, poiché Z è inferiore a 1.
Riferimenti
- Atkins, P. 2008. Chimica fisica. Editoriale Médica Panamericana. 10 - 15.
- Giancoli, D. 2006. Fisica: principi con applicazioni. 6th. Ed Prentice Hall. 242 - 243 e 314-15
- Mott, R. 2006. Fluid Mechanics. Pearson Education 13-14.
- Rex, A. 2011. Fondamenti di fisica. Pearson Education. 242-243.
- Tipler, P. (2006) Physics for Science and Technology. 5a Ed. Volume 1. Editoriale Reverté. 542.


Nessun utente ha ancora commentato questo articolo.