
Fasi del ciclo di Carnot, applicazioni, esempi, esercizi
Il Ciclo di Carnot è la sequenza dei processi termodinamici che avvengono in un motore di Carnot, un dispositivo ideale che consiste solo di processi di tipo reversibile; cioè, quelli che hanno avuto luogo, possono tornare allo stato iniziale.
Questo tipo di motore è considerato ideale, poiché manca la dissipazione, l'attrito o la viscosità che si presentano nelle macchine reali, convertendo l'energia termica in lavoro utilizzabile, sebbene la conversione non venga effettuata al 100%.

Un motore è costruito partendo da una sostanza in grado di fare lavoro, come il gas, la benzina o il vapore. Questa sostanza è soggetta a vari cambiamenti di temperatura ea sua volta subisce variazioni di pressione e volume. In questo modo è possibile muovere un pistone all'interno di un cilindro.
Indice articolo
- 1 Qual è il ciclo di carnot?
- 2 fasi del ciclo di Carnot
- 2.1 Punto di partenza
- 2.2 Primo stadio: espansione isotermica
- 2.3 Secondo stadio: espansione adiabatica
- 2.4 Terzo stadio: compressione isotermica
- 2.5 Quarto stadio: compressione adiabatica
- 3 Teorema di Carnot
- 3.1 Dimostrazione del teorema di Carnot
- 3.2 Corollario del teorema e limitazioni
- 4 esempi
- 4.1 Un pistone all'interno di un cilindro
- 4.2 Vari processi reversibili
- 4.3 Una centrale nucleare
- 5 Esercizi risolti
- 5.1 -Esempio 1: efficienza di un motore termico
- 5.2 -Esempio 2: calore assorbito e calore trasferito
- 6 Riferimenti
Qual è il ciclo di carnot?
Il ciclo di Carnot si svolge all'interno di un sistema chiamato motore Carnot o C, che è un gas ideale racchiuso in un cilindro e dotato di un pistone, che è a contatto con due sorgenti a differenti temperature T1 e TDue come quello mostrato nella figura sotto a sinistra.
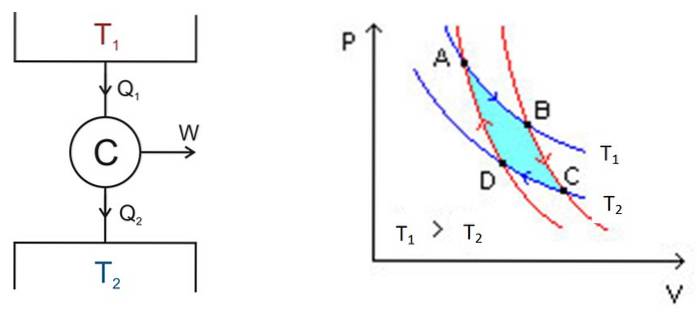
Lì, si svolgono i seguenti processi approssimativi:
- Una certa quantità di calore viene fornita al dispositivo Qiscrizione = Q1 dal serbatoio termico ad alta temperatura T1.
- Il motore C di Carnot esegue il lavoro W grazie a questo calore fornito.
- Una parte del calore utilizzato: i rifiuti QUscita, viene trasferito al serbatoio termico che si trova ad una temperatura T più bassaDue.
Fasi del ciclo di Carnot
L'analisi viene eseguita utilizzando un diagramma P-V (Pressure -Volume), come mostrato in figura 2 (figura a destra). Lo scopo del motore può essere quello di mantenere fresco il serbatoio termico 2, estraendone calore. In questo caso è un file macchina di raffreddamento. Se invece vuoi trasferire il calore al serbatoio termico 1 allora è un pompa di calore.
Il diagramma P-V mostra le variazioni di pressione - temperatura del motore in due condizioni:
- Mantenere la temperatura costante (processo isotermico).
- Nessun trasferimento di calore (isolamento termico).
I due processi isotermici devono essere collegati, cosa ottenuta mediante isolamento termico.
Punto
È possibile iniziare in qualsiasi punto del ciclo, in cui il gas ha determinate condizioni di pressione, volume e temperatura. Il gas subisce una serie di processi e può tornare alle condizioni di partenza per iniziare un altro ciclo, e l'energia interna finale è sempre la stessa di quella iniziale. Poiché l'energia è conservata:
Lavoro svolto da C = Potenza termica - Potenza termica
ΔW = Qiscrizione - QUscita
L'area all'interno di questo anello o anello, in turchese nella figura, è esattamente equivalente al lavoro svolto dal motore di Carnot.
Nella figura 2 sono segnati i punti A, B, C e D. Inizieremo dal punto A seguendo la freccia blu..
Primo stadio: espansione isotermica
La temperatura tra i punti A e B è T1. Il sistema assorbe calore dal serbatoio termico 1 e subisce un'espansione isotermica. Quindi il volume aumenta e la pressione diminuisce.
Tuttavia la temperatura rimane a T.1, da quando il gas si espande si raffredda. Pertanto, la sua energia interna rimane costante.
Secondo stadio: espansione adiabatica
Al punto B il sistema inizia una nuova espansione in cui il sistema non guadagna né perde calore. Ciò si ottiene posizionandolo in un isolamento termico come indicato sopra. Quindi è un'espansione adiabatica che continua al punto C seguendo la freccia rossa. Il volume aumenta e la pressione diminuisce fino al valore più basso.
Terzo stadio: compressione isotermica
Inizia nel punto C e termina in D. L'isolamento viene rimosso e il sistema entra in contatto con il serbatoio termico 2, la cui temperatura TDue è meno. Il sistema trasferisce il calore di scarto al serbatoio termico, la pressione inizia ad aumentare e il volume a diminuire.
Quarto stadio: compressione adiabatica
Al punto D il sistema torna in isolamento termico, la pressione aumenta e il volume diminuisce fino a raggiungere le condizioni originarie del punto A. Quindi il ciclo si ripete nuovamente..
Teorema di Carnot
Il teorema di Carnot fu postulato per la prima volta all'inizio del XIX secolo dal fisico francese Sadi Carnot. Nel 1824 Carnot, che faceva parte dell'esercito francese, pubblicò un libro in cui proponeva la risposta alla seguente domanda: in quali condizioni un motore termico ha la massima efficienza? Carnot ha quindi stabilito quanto segue:
Nessun motore termico in funzione tra due serbatoi di calore è più efficiente del motore Carnot.
Il rendimento η di un motore termico è dato dal quoziente tra il lavoro svolto W e il calore assorbito Q:
performance = lavoro svolto / calore assorbito
In questo modo, l'efficienza di qualsiasi motore termico I è: η = W / Q. Sebbene l'efficienza di un motore di Carnot R sia η '= W / Q', assumendo che entrambi i motori siano in grado di svolgere lo stesso lavoro.
Il teorema di Carnot afferma che η non è mai maggiore di η '. Altrimenti va in contraddizione con la seconda legge della termodinamica, secondo la quale è impossibile un processo in cui il risultato è che il calore esce da un corpo a temperatura più bassa per andare a una temperatura più alta senza ricevere un aiuto esterno. Perciò:
η < η'
Dimostrazione del teorema di Carnot
Per dimostrare che è così, si consideri il motore Carnot che agisce come una macchina di raffreddamento azionata da un motore I. Ciò è possibile poiché il motore Carnot funziona con processi reversibili, come specificato all'inizio..
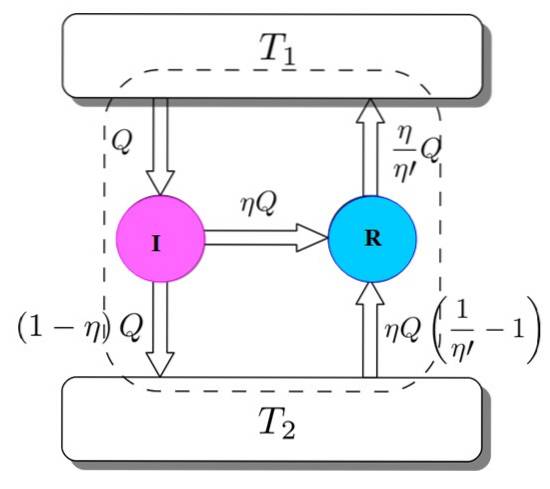
Abbiamo entrambi: I e R che lavorano con gli stessi serbatoi termici e si assumerà che η > η'. Se lungo il percorso si giunge a una contraddizione con la seconda legge della termodinamica, il teorema di Carnot è dimostrato dalla riduzione all'assurdità.
La figura 3 ti aiuta a seguire il processo. Il motore I prende una quantità di calore Q, che divide in questo modo: facendo un lavoro su R equivale a W = ηQ e il resto è il calore trasferito (1-η) Q al serbatoio termico TDue.
Poiché l'energia è conservata, tutte le seguenti condizioni sono vere:
Eiscrizione = Q = lavoro W + calore dato a TDue = ηQ + (1-η) Q = EUscita
Ora la macchina refrigerante Carnot R preleva dal serbatoio termico 2 una quantità di calore data da:
(η / η ') (1-η') Q =
Anche in questo caso l'energia deve essere conservata:
Eiscrizione = ηQ + (η / η ') (1-η') Q = (η / η ') Q = Q' = EUscita
Il risultato è il trasferimento al serbatoio termico TDue di una quantità di calore data da (η / η ') Q = Q'.
Se η è maggiore di η ', significa che più calore ha raggiunto il deposito termico di temperatura più alta di quanto avevo inizialmente preso. Poiché nessun agente esterno, come un'altra fonte di calore, ha partecipato, l'unico modo in cui potrebbe accadere è che il serbatoio termico più freddo ceda il calore..
Questo è in disaccordo con la seconda legge della termodinamica. Si conclude quindi che non è possibile che η' è minore di η, quindi il motore non posso avere più efficienza della macchina di Carnot R.
Corollario del teorema e limitazioni
Il corollario del teorema di Carnot afferma che due macchine di Carnot hanno la stessa efficienza se funzionano entrambe con gli stessi serbatoi termici..
Ciò significa che, indipendentemente dalla sostanza, le prestazioni sono indipendenti e non possono essere aumentate modificandole..
La conclusione dall'analisi di cui sopra è che il ciclo di Carnot è la parte superiore idealmente raggiungibile del processo termodinamico. In pratica sono molti i fattori che diminuiscono l'efficienza, ad esempio il fatto che l'isolamento non è mai perfetto e nelle fasi adiabatiche c'è effettivamente scambio termico con l'esterno.
Nel caso di un'auto, il blocco motore si surriscalda. D'altra parte, la miscela di benzina e aria non si comporta esattamente come un gas ideale, che è il punto di partenza del ciclo di Carnot. Questo per citare solo alcuni fattori che causeranno una drastica riduzione delle prestazioni.
Esempi
Un pistone all'interno di un cilindro
Se il sistema è un pistone racchiuso in un cilindro come in figura 4, il pistone si alza durante l'espansione isotermica, come si può vedere nel primo diagramma all'estrema sinistra, e sale anche durante l'espansione adiabatica.
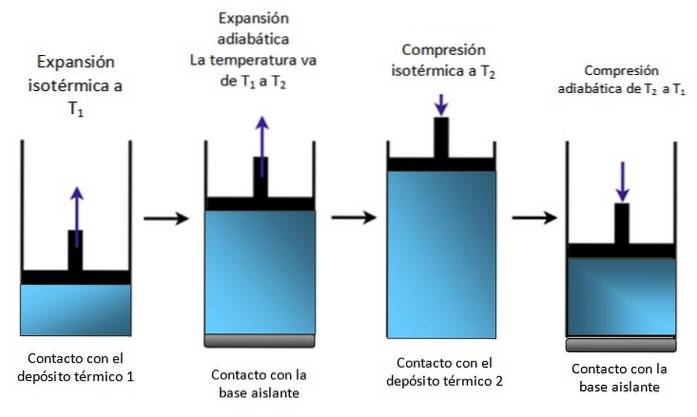
Viene quindi compresso isotermicamente, cedendo calore e continua a comprimersi adiabaticamente. Il risultato è un movimento in cui il pistone sale e scende all'interno del cilindro e che può essere trasmesso ad altre parti di un particolare dispositivo, come ad esempio il motore di un'auto, che produce coppia, o un motore a vapore.
Vari processi reversibili
Oltre all'espansione e compressione di un gas ideale all'interno di una bombola, esistono altri processi reversibili ideali con i quali è possibile configurare un ciclo di Carnot, ad esempio:
- Movimenti avanti e indietro in assenza di attrito.
- Una molla ideale che si comprime e si decomprime e non si deforma mai.
- Circuiti elettrici in cui non sono presenti resistenze per dissipare energia.
- Cicli di magnetizzazione e smagnetizzazione in cui non ci sono perdite.
- Carica e scarica di una batteria.
Una centrale nucleare
Sebbene sia un sistema molto complesso, una prima approssimazione di ciò che è necessario per produrre energia in un reattore nucleare è la seguente:
- Una sorgente termica, costituita da un materiale in decomposizione radioattiva come l'uranio.
- Il dissipatore di calore freddo o il serbatoio che sarebbe l'atmosfera.
- Il "motore Carnot" che utilizza un fluido, quasi sempre acqua di rubinetto, a cui viene fornito calore dalla sorgente termica per convertirlo in vapore.
Quando il ciclo viene eseguito, l'energia elettrica viene ottenuta come lavoro netto. Quando viene trasformata in vapore ad alta temperatura, l'acqua viene fatta raggiungere una turbina, dove l'energia si trasforma in movimento o energia cinetica.
La turbina a sua volta aziona un generatore elettrico che trasforma l'energia del suo movimento in energia elettrica. Oltre al materiale fissile come l'uranio, i combustibili fossili possono ovviamente essere utilizzati come fonte di calore..
Esercizi risolti
-Esempio 1: efficienza di un motore termico
L'efficienza di un motore termico è definita come il quoziente tra il lavoro in uscita e il lavoro in ingresso, e quindi è una quantità adimensionale:
Massima efficienza = (Qiscrizione - Q Uscita) / Qiscrizione
Denotando la massima efficienza come emax, è possibile dimostrare la sua dipendenza dalla temperatura, che è la variabile più semplice da misurare, come ad esempio:
emax = 1 - (TDue/ T1)
DoveDue è la temperatura del pozzetto e T1 è la temperatura della fonte di calore. Poiché quest'ultimo è maggiore, l'efficienza risulta essere sempre inferiore a 1.
Supponiamo di avere un motore termico in grado di funzionare nei seguenti modi: a) Tra 200 K e 400 K, b) Tra 600 K e 400 K. Qual è l'efficienza in ciascun caso?
Soluzione
a) Nel primo caso l'efficienza è:
emax1 = 1 - (200/400) = 0,50
b) Per la seconda modalità l'efficienza sarà:
emax2 = 1- (400/600) = 0,33
Sebbene la differenza di temperatura sia la stessa tra le due modalità, l'efficienza non lo è. E ancora più notevole è che la modalità più efficiente funziona a una temperatura più bassa..
-Esempio 2: calore assorbito e calore rilasciato
Un motore termico efficiente al 22% produce 1.530 J di lavoro. Trova: a) La quantità di calore assorbita dal serbatoio termico 1, b) La quantità di calore scaricata nel serbatoio termico 2.
a) In questo caso si usa la definizione di efficienza, essendo disponibile il lavoro svolto, non le temperature dei serbatoi termici. Un'efficienza del 22% significa che e max = 0.22, quindi:
Massima efficienza = Lavoro / Qiscrizione
La quantità di calore assorbita è precisa Qiscrizione, così chiarendo abbiamo:
Qiscrizione = Lavoro / Efficienza = 1530 J / 0,22 = 6954,5 J
b) La quantità di calore trasferita al serbatoio più freddo si trova da ΔW = Qiscrizione - QUscita
QUscita = Qiscrizione - ΔW = 6954,5 -1530 J = 5424,5 J.
Un altro modo è da emax = 1 - (TDue/ T1). Poiché le temperature non sono note, ma sono legate al calore, l'efficienza può essere espressa anche come:
emax = 1 - (Qceduto/ Qassorbito)
Riferimenti
- Bauer, W. 2011. Fisica per l'ingegneria e le scienze. Volume 1. Mc Graw Hill. 654-657
- Energia nucleare. Funzionamento di una centrale nucleare. Estratto da: energia-nuclear.net
- Serway, R., Jewett, J. (2008). Fisica per la scienza e l'ingegneria. Volume 1. 7th. Ed. Cengage Learning. 618-622.
- Tippens, P. 2011. Fisica: concetti e applicazioni. 7a edizione. MacGraw Hill. 414-416.
- Walker, J. 2008. Fisica. 4a Ed. Addison Wesley. 610-630


Nessun utente ha ancora commentato questo articolo.