
Processo del ciclo di Brayton, efficienza, applicazioni, esercizi
Il Ciclo di Brayton è un ciclo termodinamico che consiste di quattro processi e viene applicato a un fluido termodinamico comprimibile come un gas. La sua prima menzione risale alla fine del XVIII secolo, anche se passò del tempo prima che fosse sollevata per la prima volta da James Joule. Questo è il motivo per cui è noto anche come ciclo Joule..
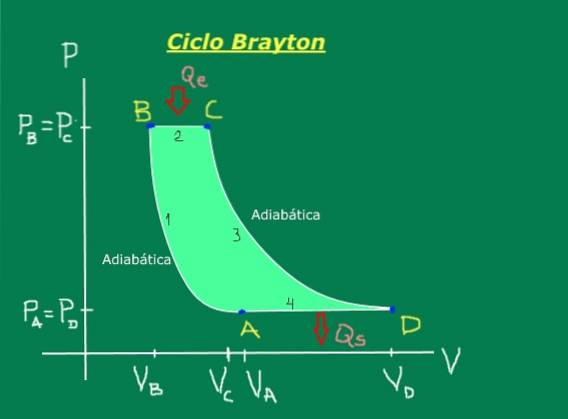
Consiste delle seguenti fasi, che sono convenientemente illustrate nel diagramma pressione-volume di figura 1: compressione adiabatica (non viene scambiato calore), espansione isobarica (avviene a pressione costante), espansione adiabatica (non viene scambiato calore) e compressione isobarica (si verifica a pressione costante).
Indice articolo
- 1 Processo e descrizione
- 1.1 Ammissione
- 1.2 Compressione
- 1.3 Combustione
- 1.4 Espansione
- 1.5 Scarico
- 2 Efficienza in funzione di temperatura, calore e pressione
- 2.1 Calore in entrata, calore in uscita ed efficienza
- 2.2 Calore e pressione nel ciclo di Brayton
- 2.3 Risultato semplificato
- 2.4 Efficienza in funzione del rapporto di pressione
- 3 Applicazioni
- 4 Esercizi risolti
- 4.1 -Esercizio 1
- 4.2 -Esercizio 2
- 5 Riferimenti
Processo e descrizione
Il ciclo Brayton è il ciclo termodinamico ideale che viene applicato al meglio per spiegare il funzionamento termodinamico delle turbine a gas e del mix aria-carburante, utilizzato per la generazione di energia elettrica e nei motori degli aeromobili.
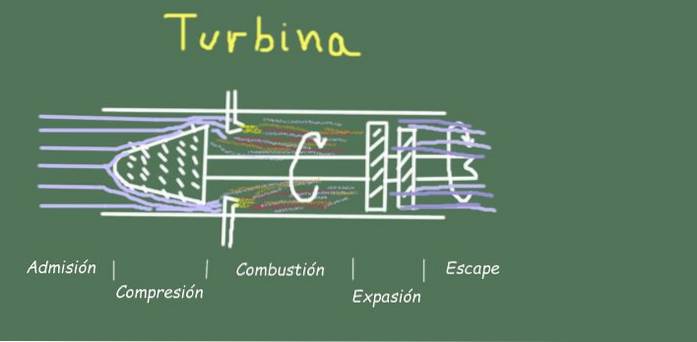
Ad esempio, nel funzionamento di una turbina ci sono diverse fasi nel flusso di gas operativo, che vedremo di seguito.
Ammissione
Consiste nell'ingresso di aria a temperatura e pressione ambiente attraverso l'apertura di ingresso della turbina.
Compressione
L'aria viene compressa ruotando le pale contro le pale fisse nella sezione del compressore della turbina. Questa compressione è così veloce che praticamente non c'è scambio di calore, quindi è modellata dal processo adiabatico AB del ciclo di Brayton. L'aria all'uscita del compressore ha aumentato la sua pressione e temperatura.
Combustione
L'aria viene miscelata con gas propano o combustibile polverizzato che viene introdotto attraverso gli iniettori della camera di combustione. La miscela produce una reazione chimica di combustione.
Questa reazione è ciò che fornisce il calore che aumenta la temperatura e l'energia cinetica delle particelle di gas che si espandono nella camera di combustione a pressione costante. Nel ciclo di Brayton questo passaggio è modellato con il processo BC che avviene a pressione costante.
Espansione
Nella sezione della turbina stessa, l'aria continua ad espandersi contro le pale della turbina, facendola ruotare e producendo lavoro meccanico. In questa fase l'aria abbassa la sua temperatura ma senza praticamente scambiare calore con l'ambiente..
Nel ciclo di Brayton questo passaggio viene simulato come un processo di espansione adiabatica CD. Una parte del lavoro della turbina viene trasferita al compressore e l'altra viene utilizzata per azionare un generatore o un'elica.
Fuga
L'aria in uscita è ad una pressione costante pari alla pressione ambiente e cede calore all'enorme massa d'aria esterna, quindi in breve tempo assume la stessa temperatura dell'aria in ingresso. Nel ciclo Brayton questo passaggio viene simulato con il processo DA a pressione costante, chiudendo il ciclo termodinamico.
Efficienza in funzione di temperatura, calore e pressione
Ci proponiamo di calcolare l'efficienza del ciclo di Brayton, per il quale partiamo dalla definizione di esso.
In un motore termico, l'efficienza è definita come il lavoro netto svolto dalla macchina diviso per l'energia termica fornita.

Il primo principio della termodinamica afferma che il calore netto contribuito a un gas in un processo termodinamico è uguale alla variazione dell'energia interna del gas più il lavoro svolto da esso..
Ma in un ciclo completo la variazione dell'energia interna è nulla, quindi il calore netto apportato al ciclo è uguale al lavoro netto svolto..

Calore in entrata, calore in uscita ed efficienza
L'espressione precedente ci permette di scrivere l'efficienza in funzione del calore assorbito o entrante Qe (positivo) e del calore trasferito o uscente Qs (negativo).

Calore e pressione nel ciclo di Brayton
Nel ciclo di Brayton, il calore entra nel processo isobarico BC ed esce nel processo isobarico DA.
Supponendo che n moli di gas a pressione costante siano alimentate con calore sensibile Qe nel processo BC, la sua temperatura aumenta da Tb a Tc secondo la seguente relazione:

Calore in uscita Qs può essere calcolato in modo simile dalla seguente relazione che si applica al processo a pressione costante DA:

Sostituendo queste espressioni nell'espressione che ci dà l'efficienza in funzione del calore in ingresso e in uscita, apportando le opportune semplificazioni, si ottiene la seguente relazione di efficienza:

Risultato semplificato
È possibile semplificare il risultato precedente se ne teniamo conto Pa = Pd E allora Pb = Pc poiché i processi AD e BC sono isobarici, cioè alla stessa pressione.
Inoltre, poiché i processi AB e CD sono adiabatici, il rapporto di Poisson è soddisfatto per entrambi i processi:

Dove gamma rappresenta il quoziente adiabatico, ovvero il quoziente tra la capacità termica a pressione costante e la capacità termica a volume costante.
Usando queste relazioni e la relazione dall'equazione di stato dei gas ideali possiamo ottenere un'espressione alternativa per il rapporto di Poisson:

Come lo sappiamo Pa = Pd E allora Pb = Pc sostituendo e dividendo elemento per elemento si ottiene il seguente rapporto tra le temperature:

Se ogni membro dell'equazione precedente viene sottratto dall'unità, la differenza viene risolta e i termini sono disposti, si può dimostrare che:


Prestazioni in funzione del rapporto di pressione
L'espressione ottenuta per l'efficienza del ciclo Brayton in funzione delle temperature può essere riscritta per essere formulata in funzione del quoziente di pressione all'uscita e all'ingresso del compressore.
Ciò si ottiene se il rapporto di Poisson tra i punti A e B è noto in funzione della pressione e della temperatura, ottenendo che l'efficienza del ciclo si esprime come segue:

Un tipico rapporto di pressione è 8. In questo caso il ciclo Brayton ha una resa teorica del 45%..
Applicazioni
Il ciclo di Brayton come modello viene applicato alle turbine a gas che vengono utilizzate negli impianti termoelettrici per muovere i generatori che producono elettricità.
È anche un modello teorico che ben si adatta al funzionamento dei motori turboelica utilizzati negli aeromobili, ma non è affatto applicabile nei turboreattori degli aeromobili..
Quando si desidera massimizzare il lavoro prodotto dalla turbina per muovere i generatori o le eliche di un aereo, viene applicato il ciclo di Brayton..

Nei turboreattori degli aerei, invece, non è interessante convertire l'energia cinetica dei gas di combustione per produrre lavoro, che sarebbe appena sufficiente per ricaricare il turbocompressore.
Al contrario, è importante ottenere la massima energia cinetica possibile del gas espulso, in modo che secondo il principio di azione e reazione si ottenga la quantità di moto dell'aereo..
Esercizi risolti
-Esercizio 1
Una turbina a gas utilizzata nelle centrali termoelettriche ha una pressione all'uscita del compressore di 800 kPa. La temperatura del gas in ingresso è quella ambiente ed è di 25 gradi Celsius e la pressione è di 100 kPa.
Nella camera di combustione la temperatura sale fino a 1027 gradi Celsius per entrare nella turbina.
Determinare l'efficienza del ciclo, la temperatura del gas all'uscita del compressore e la temperatura del gas all'uscita della turbina.
Soluzione
Avendo la pressione del gas all'uscita del compressore e sappiamo che la pressione in ingresso è quella atmosferica, allora è possibile ottenere il rapporto di pressione:
r = Pb / Pa = 800 kPa / 100 KPa = 8
Poiché il gas con cui opera la turbina è una miscela di aria e gas propano, il coefficiente adiabatico viene quindi applicato per un gas ideale biatomico, cioè un gamma di 1,4.
L'efficienza sarebbe quindi calcolata in questo modo:
Dove abbiamo applicato la relazione che dà l'efficienza del ciclo Brayton in funzione del rapporto di pressione nel compressore.

Calcolo della temperatura
Per determinare la temperatura all'uscita del compressore, ovvero quale sia la temperatura con cui il gas entra nella camera di combustione, applichiamo il rapporto del rendimento con le temperature di ingresso e uscita del compressore.
Se risolviamo la temperatura Tb da tale espressione, otteniamo:

Come dati per l'esercizio abbiamo che dopo la combustione la temperatura sale a 1027 gradi Celsius, per entrare nella turbina. Parte dell'energia termica del gas viene utilizzata per muovere la turbina, quindi la temperatura alla sua uscita deve essere inferiore.
Per calcolare la temperatura all'uscita della turbina utilizzeremo una relazione tra la temperatura ottenuta in precedenza:

Da lì risolviamo per Td per ottenere la temperatura all'uscita della turbina. Dopo aver eseguito i calcoli, la temperatura ottenuta è:
Td = 143,05 gradi Celsius.
-Esercizio 2
Una turbina a gas segue il ciclo di Brayton. Il rapporto di pressione tra l'ingresso e l'uscita del compressore è 12.
Supponiamo che la temperatura ambiente sia di 300 K. Come dati aggiuntivi è noto che la temperatura del gas dopo la combustione (prima dell'ingresso nella turbina) è di 1000K.
Determinare la temperatura all'uscita del compressore e la temperatura all'uscita della turbina. Determina anche quanti chilogrammi di gas circolano attraverso la turbina in ogni secondo, sapendo che la sua potenza è di 30 KW.
Assumiamo costante il calore specifico del gas e prendiamo il suo valore a temperatura ambiente: Cp = 1.0035 J / (kg K).
Supponiamo inoltre che l'efficienza di compressione nel compressore e l'efficienza di decompressione nella turbina sia del 100%, il che è un'idealizzazione perché in pratica si verificano sempre perdite..
Soluzione
Per determinare la temperatura all'uscita del compressore, conoscendo la temperatura in ingresso, dobbiamo ricordare che è una compressione adiabatica, quindi il rapporto di Poisson può essere applicato per il processo AB.



Per qualsiasi ciclo termodinamico, il lavoro netto sarà sempre uguale al calore netto scambiato nel ciclo..

Il lavoro netto per ciclo operativo può quindi essere espresso in funzione della massa di gas che circolava in quel ciclo e delle temperature.

In questa espressione m è la massa di gas che circolava attraverso la turbina in un ciclo operativo e Cp calore specifico.
Se prendiamo la derivata rispetto al tempo dell'espressione precedente, otteniamo la potenza media netta in funzione della portata massica.

Sgombrare punto m, e sostituendo le temperature, la potenza e la capacità termica del gas, si ottiene una portata massica di 1578,4 kg / s.
Riferimenti
- Alfaro, J. Thermodynamic Cycles. Recupero da: fis.puc.cl.
- Fernandez J.F. Ciclo di Brayton. Turbina a gas. U.T.N. (Mendoza). Estratto da: edutecne.utn.edu.ar.
- Università di Siviglia. Dipartimento di fisica. Ciclo di Brayton. Recupero da: laplace.us.es.
- Táchira National Experimental University. Fenomeni di trasporto. Cicli di potenza a gas. Recupero da: unet.edu.ve.
- Wikipedia. Ciclo di Brayton. Estratto da: wikiwand.com
- Wikipedia. Turbina a gas. Estratto da: wikiwand.com.



Nessun utente ha ancora commentato questo articolo.